段超霞，田学民

（1.国家知识产权局专利局专利审查协作 广东中心，广州510530；2.中国石油大学 信息与控制工程学院，山东 青岛266580）

神经网络由于其良好的非线性逼近性能而广泛应用于非线性系统的建模［1］。在使用神经网络解决给定的实际逼近问题时，激活函数的选择对神经网络的结构和逼近性能有很大影响，常用的激活函数有sigmoid函数、高斯函数、双曲正切函数等。尽管这些函数在实际建模过程中已得到了广泛应用，但也存在一些缺点，如过训练，易陷入局部极小点，学习过程非常耗时等。基于傅立叶分析理论而建立的傅立叶神经网络［2－3］FoNN（Fourier Neural Network）则能避免上述问题，它以正交傅立叶复指数函数为激活函数，使得网络的输出权值为给定目标函数的频谱，且网络结构也可依据系统的物理特性确定。训练FoNN时，仅需对输出权重进行调整，训练参数少，因而收敛速度快；且正交激活函数的存在，使训练更易收敛到全局极值点［4］。由于FoNN使用正交的傅立叶复指数函数作为激活函数，当用于控制时，能与闭环系统的频域响应紧密联系起来，因而ZUO Wei等将自适应规则、迭代学习控制与FoNN结合起来应用到非线性系统的跟踪控制中［5－8］。

在FoNN中，影响其性能的关键因素是基频和隐含层神经元数目。如果基频选择较小，那么需要的隐含层节点就多，这样就会增加网络的复杂度；若基频选择较大，则会影响网络的性能。因此，采用FoNN进行建模，选择基频及隐含层节点的数目则成为关键问题。现有的方法大多数是基频和隐含层神经元数目按照系统的周期和带宽确定的。但在实际工业过程中，大多数过程是非周期过程，而且过程的带宽也不易确定，限制了FoNN在工业过程建模中的应用。因此，寻找合适方法确定FoNN结构能进一步扩展FoNN的应用。

笔者针对FoNN基频选取及隐含层神经元数目确定问题，提出将其当作是激活函数的选择问题，给定一个较小的基频，把傅立叶级数中的一系列关于基频整数倍的正余弦函数作为激活函数的选择范围，然后采用正交最小二乘OLS（Orthogonal Least Square）算法进行选择，保留对建模贡献显著的函数，剔除贡献小的函数，从而确定FoNN的激活函数，简化网络结构。最后，以聚合反应器为对象进行了仿真研究，仿真结果验证了OLS算法对FoNN训练的可行性和有效性。

1 基于OLS的FoNN结构选取方法

1.1 傅立叶神经网络

FoNN是依据傅立叶级数及其逼近理论和神经网络的理论而建立的。FoNN将一组正交傅立叶基函数作为三层前向神经网络隐含层的激活函数，以其加权和为网络的输出，结构如图1所示。

图1 FoNN结构

图1中，WIH，k——输入节点连接到第k个隐含层节点的权值，其值为1，k＝－M，…，0，…M，k为整数；激活函数σk（x（k））＝eikωx（k），ω 为基频；WOH，k——第k个隐含层节点连接到输出节点的权值。FoNN的输出为

在实际应用中，复函数eikωx（k）无法实现，可以利用Euler公式对其进行变换，使用正余弦函数来代替，则FoNN的输出可以表示为

式中：正余弦函数cos（nωx（k）），sin（nωx（k））——FoNN激活函数，n＝1，…，M；wi——输出权重，i＝0，…，2 M。由于FoNN采用傅立叶复指数函数作为激活函数，wi也可看作给定目标函数的频谱。由傅立叶级数逼近理论可知，FoNN能以任意精度逼近任何非线性函数。

影响FoNN逼近性能的关键是基频选取和隐含层神经元的数目。通常，ω是根据系统周期T确定，即ω＝2π／T；隐藏层神经元数目M则根据系统的有限输入带宽ωc选择，满足M ≤Mc，其中，Mc＝ωc／ω［7］。在实际系统中，大多数都是非周期的系统，周期难以确定；有限输入带宽也不易确定；即使基频和带宽确定，FoNN隐含层神经元数目只有大致选择范围。因此为使FoNN具有更好的逼近能力，则需要尽可能多的神经元，使其结构更复杂，训练时调整参数增加，训练速度减慢；FoNN节点数目越多，不可避免地存在冗余节点，这些节点对网络的性能影响并不大，但其存在会使得FoNN结构更加复杂，但FoNN神经元数目选择较少时，会影响FoNN逼近性能。因此，在采用FoNN进行建模时，如何选择基频和隐含层神经元数目则成为关键问题。笔者采用OLS算法来解决这一问题。

1.2 基于OLS算法的FoNN激活函数选取

OLS算法来源于线性回归模型。文献［9］将其用于RBF神经网络中心的选择。令网络的训练样本集对为 ｛x（k），y（k）｝，k＝1，…，N，N 为样本数目。将FoNN输出式（2）变换为

式 中：y（k）——实 际 输 出；θi——网 络 权 重；2 M——隐藏层神经元数目；pi（k）——FoNN 关于x（k）的回归算子。

假设误差信号ε（k）与pi（k）不相关，将FoNN模型写成矩阵方程式的形式：

式中：y＝ ［y（1），y（2），…，y（N）］T；P＝ ［p0，p1，…，p2M］；pi＝ ［pi（1），pi（2），…，pi（N）］T，0≤i≤2 M；θ＝ ［θ0，θ1，…，θ2M］T；e＝ ［ε（1），ε（2），…，ε（N）］T。

求解式（4）的关键问题是回归矢量pi的选择。一旦回归矩阵P已定，模型参数就可由最小二乘方法求解得到。确定一组激活函数φi对应于输入样本就能得到一个pi。每个激活函数对降低残差的贡献不同，要选择贡献显著的函数，剔除贡献小的函数。通过正交化pi，分析pi对降低残差的贡献，选择合适的回归矢量，并根据误差性能指标，确定回归算子个数Ms。用传统的Gram Sechmidt正交化方法对P进行正交 －三角分解，即P＝UA，A是一个（2 M＋1）×（2 M＋1）维的上三角矩阵，且主对角元素为1；U＝［u0，u1，…，u2M］，uTiuj＝0，i≠j。所以，回归方程（4）可转化为

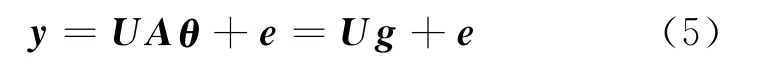
则正交最小二乘解为

假设式（7）中的矢量U g和e互不相关，则输出响应的能量可表示为

上式两边除以yTy，得

式中：εi—— 误差衰减比，εi＝g2iuTiui／yTy；q——允许误差，q＝eTe／yTy。

由式（6）知，gi仅与y 和ui有关，y已知，εi由ui决定。在采用OLS算法训练FoNN时，为获得良好训练效果，要使q尽可能小。由式（8）可知，当εi越大，q越小，要选择使εi尽可能大的回归算子ui（pi），此时，pi对应函数即为所要选的FoNN 激活函数。

OLS算法训练FoNN的任务是通过对训练样本学习，选择合适的回归矢量pi及其个数Ms，使FoNN输出满足误差要求。其选取步骤如下：

Step 1：给定基频ω，给出预选的隐含层节点个数 Mr，相 应的激活函数选择范围设定允许误差q；

Step 2：根据选择的激活函数用输入样本矢量xi，i＝1，…，N，计算回归矩阵P；

Step 3：开始迭代，第k步时，采用 Gram Sechmidt正交化方法，对回归矩阵各列pi，i＝1，…，2 M 正交化，得，由式（6）计算，利用计算，选择最大，令er rk＝，并记录和。此时对应pi即为所选的第k个回归矢量，选出pi；

Step5：pi确定后，P，U 和已知，由P＝UA计算上三角矩阵A，由方程求出输出权值θ的估计

1.3 仿真研究

以甲基丙烯酸甲酯反应的聚合反应器为研究对象，该反应以偶氮二异丁腈为引发剂，甲苯为溶剂，引发剂流量FI为系统输入，聚合物的平均相对分子质量（MW）作为系统输出。该聚合反应器的模型可描述为下述的非线性常微分方程：

系统输出：MW（t）＝DI（t）／D0（t）。

式中：F——溶剂流量；Cm，CI，D0，DI——系统的状态变量；T——冷却水温度；聚合反应器参数取值选自文献［10］。

该过程动静特性符合 Wiener模型的特点［10］，因而采用Wiener模型建立该对象的模型。Wiener模 型 的 线 性 动 态 部 分 由 G（q－1）＝表示，经参数辨识得b1＝－0.038 5，b2＝0.015 3，a1＝－1.296 9，a2＝0.386 3。笔者主要对 Wiener模型的非线性部分进行建模，在辨识非线性静态部分时，随机产生如图2～3所示的训练和测试数据组，每组包含数据500个。

考虑到图2～3中的输入输出数据范围相差太大，需要对数据进行预处理，将其转换为相同数量级，再用来训练神经网络，即令y＝0.000 1（MWMW0），u ＝ 100（qVI－qVI，0），MW0＝20t／kmol，qVI，0＝0.028 331m3／h。在神经网络训练中，误差平方和为性能评价函数：y（k）为神经网络输出，yd（k）为训练目标。

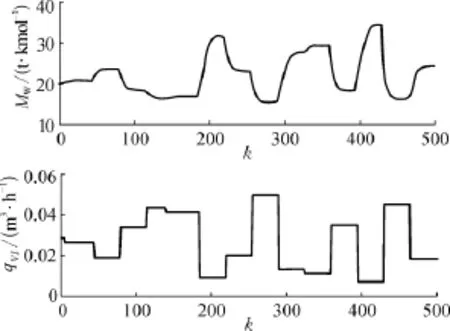
图2 训练数据

图3 测试数据

首先，为验证文中所提方法的可行性，采用扩展卡尔曼滤波 EKF（Extend Kalman Filter）训练FoNN，改变基频和隐含层神经元个数，观察对训练结果的影响。为验证训练算法的鲁棒性，在预处理后的训练和测试数据中分别加入均方差为0.02的白噪声，观察训练效果。EKF训练中，迭代200次。训练结果见表1所列。

从表1可知，采用EKF算法对FoNN进行训练，当ω＝0.1时，需要40个隐藏层神经元，训练FoNN的SSE才能达到0.5左右，才具有较好的逼近性能；增大基频至ω＝1时，仅需6个隐含层神经元就能获得较好的训练结果，此时再增加神经元数目至10或20个时，训练精度未显著提高。因此，在增加的隐含层神经元中，有一些对网络逼近性能影响不大，却使网络结构更复杂，所以采取合适方法对FoNN结构进行简化，仍保持FoNN逼近性能，是可行的。

采用OLS算法对FoNN进行训练，先给出一个较小的基频，再给出一系列的正余弦函数作为激活函数的选择范围，由OLS算法选择对FoNN逼近性能贡献显著的函数作为FoNN激活函数。笔者选择ω＝0.01，激活函数的选择范围是［cosωx，sinωx ］到 ［cos 250ωx，sin 250ωx］的500组正余弦函数的集合。根据图2～3中的训练数据和测试数据采用OLS算法对FoNN进行训练，结果列入表2中，并将表1神经元数目为6时训练结果作为对比结果列入表2中。

同时，为进一步验证OLS算法训练FoNN的效果，再使用以双曲正切函数为激活函数的多层感知机（MLP）网络描述 Wiener模型非线性部分，采用EKF算法对 MLP进行训练［11］，结果见表2所列。

由表2可以看出，采用OLS算法对FoNN进行训练时，仅需要4个隐含层神经元就能得到良好的训练精度，且当噪声存在时，FoNN网络具有良好的抵抗噪声能力。将基于EKF算法训练的FoNN结果与基于OLS算法的FoNN训练结果比较，发现OLS算法在训练精度和抵抗噪声方面都优于基于EKF算法的FoNN。将采用OLS算法训练的FoNN的SSE与采用EKF算法训练的MLP网络的SSE进行比较，得出当无噪声存在时，基于EKF的MLP网络的训练精度要优于OLS算法的FoNN；当噪声存在时，基于EKF算法的MLP网络抵抗噪声的能力低于基于OLS的FONN。通过对三种结构的可调整参数进行比较，基于OLS算法的FoNN需要调整参数最少。从图4的测试结果可以进一步验证，采用OLS算法确立FoNN结构，FoNN具有良好逼近性能。

因此，由以上仿真结果可以说明，采用OLS算法能够确立FoNN结构，它不仅能简化FoNN网络的结构，而且使FoNN具有更好的逼近性能和抵抗噪声的能力。

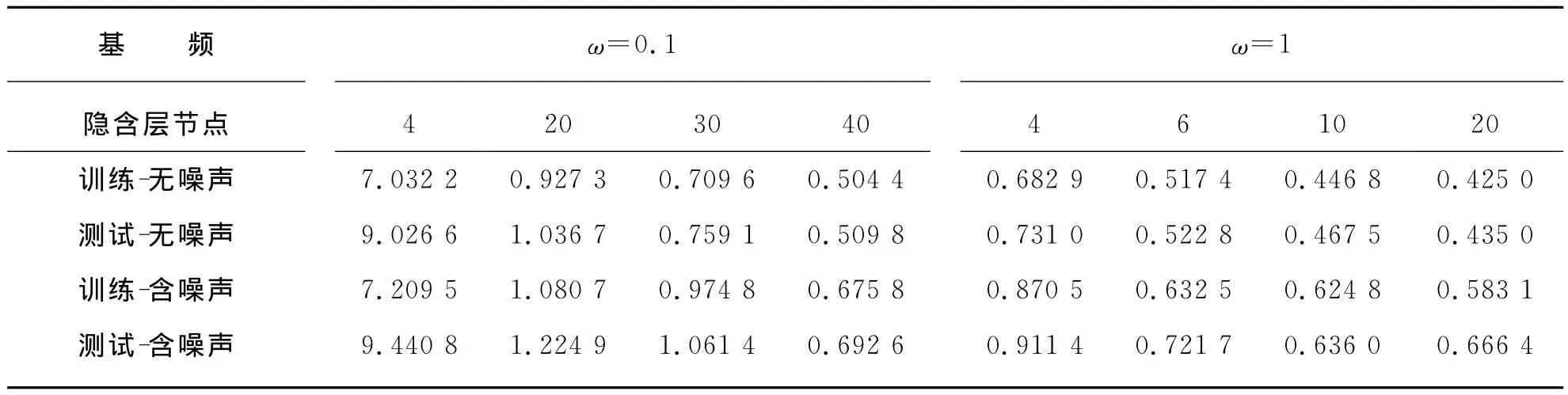
表1 采用EKF算法训练FoNN，改变基频和隐含层节点的训练及测试结果

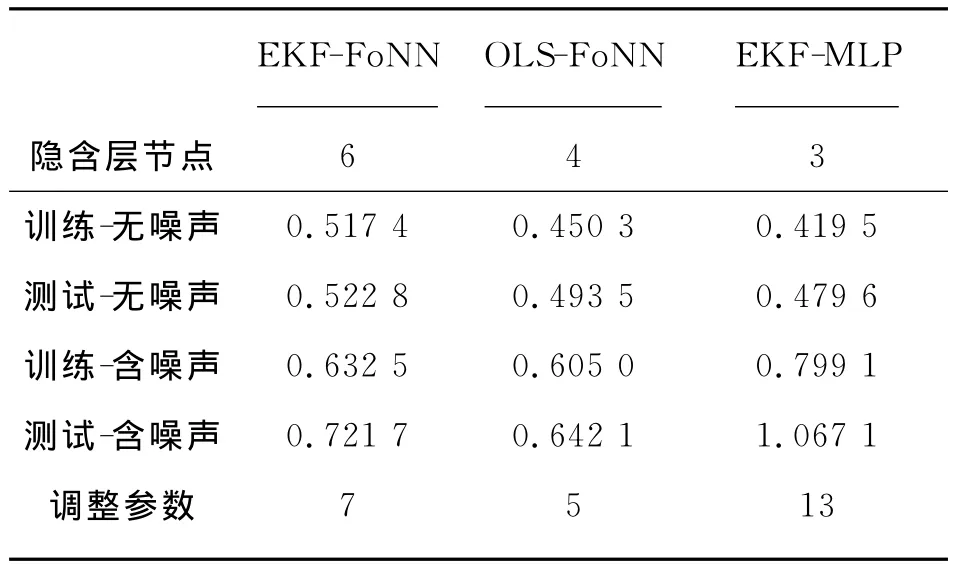
表2 采用EKF－MLP，EKF－FoNN及OLS－FoNN算法训练及测试的SSE

图4 测试曲线示意

2 结束语

本文将OLS算法用于对FoNN的结构确定，解决了FoNN的基频选取及隐含层神经元数目难以确定的问题。OLS算法选取对FoNN逼近性能贡献显著函数作为激活函数，剔除贡献小函数，简化了网络结构。对聚合反应器仿真结果表明，采用OLS算法能够建立精简的FoNN，使用该方法对非线性系统建模时，它能够在保证逼近精度时，建立精简的FoNN结构，并使其在收敛速度、训练精度、抗噪声等方面优于基于EKF算法的FoNN及MLP神经网络。

［1］JANCZAK A.Identification of Nonlinear Systems Using Neural Networks and Polynomial Models：A Block－Oriented Approach，Lecture Notes in Control and Information Sciences［M］.Berlin：Springer，2005：16－19.

［2］PELAGOTTI A，PIURE V.Neural Spectral Composition for Function Approximation［C］／／In Proc.IEEE－INNS Int.Joint Conf.Neural Networks IJCNN97.Houston，TX，1997：860－864.

［3］卢洪涛，戚飞虎.多维离散傅立叶变换神经网络函数逼近［J］.上海交通大学学报，2000，34（07）：956－958.

［4］ZUO Wei.Fourier Neural Network Based on Tracking Control for Nonlinear System［D］.Hong Kong：The Hong Kong University of Science and Technology，2008：22－32.

［5］ZUO Wei，CAI Lilong.Adaptive Fourier Neural Network Based Control for a Class of Uncertain Nonlinear Systems［J］.IEEE Transactions on Neural Networks，2008，19（10）：1689－1701.

［6］ZUO Wei， YANG Zhu，CAI Lilong.Fourier－Neural－Network－Based Learning Control for a Class of Nonlinear Systems with Flexible Components［J］.IEEE Transactions on Neural Networks，2009，20（01）：139－151.

［7］ZUO Wei，CAI Lilong.A New Iterative Learning Controller Using Variable Structure Fourier Neural Network［J］.IEEE Transactions on Systems，Man and Cybernetics－Part B：Cybernetics，2010，40（02）：458－468.

［8］ZUO Wei，CAI Lilong.Tracking Control of Nonlinear Systems Using Fourier Neural Network［C］／／Proceedings of the 2005IEEE／ASME International Conference on Advanced Intelligent Mechatronics.Monterey，CA，2005：670－675.

［9］CHEN Sheng，GRANT P M，COWAN C F N.Orthogonal Least Squares Learning Algorithm for Radial Basis Function Networks ［J］.IEEE Transaction on Neural Network，1991，2（02）：302－309.

［10］LAWRYN'CZUK M.Computationally Efficient Nonlinear Predictive Control Based on Neural Wiener Model ［J］.Neuro Computing，2010（74）：401－417.

［11］YANG Huizhong，LI Jiang， DING Feng.A Neural Network Learning Algorithm of Chemical Process Modeling Based on the Extended Kalman Filter ［J］.Neuro Computing，2007（70）：625－632.