王占丰，陈鸣，邢长友，白华利，魏祥麟

（解放军理工大学 指挥自动化学院，江苏 南京 210007）

1 引言

在因特网时延空间中，违反三角形不等式(TIV,triangle inequality violation)的现象已被许多网络测量数据集所证实[1～5]。TIV是指以节点间的往返时延(RTT, round trip time)作为距离测度，则网络中任意3个节点构成的三角形中2边之和不大于第3个边。通常认为 TIV现象是由低效路由策略（routing inefficiency）和网络结构导致的[1～3]。TIV现象使得因特网时延建模变得举步维艰，TIV现象严重的数据集嵌入时误差较大[4]。如何消除或缓解TIV的影响成为当前因特网时延空间建模（或网络坐标系统）研究的热点。

文献[1]利用时延较小时 TIV严重性较轻这一现象，提出了一种基于时延阈值的层次化 Vivaldi因特网时延空间模型。文献[5]进一步分析了时延大小和TIV的关系，发现这种关系并不明显，为减小TIV导致的预测误差，每个节点在选择邻居节点时，选择那些使预测误差最小的节点作为邻居节点，以获得最佳嵌入坐标。文献[6]分析了因特网时延空间的聚簇（cluster）特性，指出TIV在不同的节点簇之间比较严重，而在簇内则比较轻。这种方法虽然保证了坐标系统的稳定性，却限制了该算法的适用范围。文献[7]同样利用因特网时延空间TIV的聚簇特性，提出了一种双层因特网时延空间模型。文献[8]使用一种基于决策树的有监督学习方法来判定TIV是否发生，其原理是将时延系统的预测值与实际测量值的统计量作为输入样本，通过标记的TIV来训练决策树，最后给出一颗TIV判定树。

上述算法尽管表现形式不同，但都是通过将因特网时延空间划分为不同粒度的子空间，以减轻数据集中的TIV严重程度。然而，对于如何减少划分后数据子集内的TIV比例和严重程度却没有提出明确的解决方案。本文主要贡献是分析了TIV导致因特网时延空间嵌入误差的机理，引入一种基于指数变换的空间修复方法，提了一种基于空间修复的因特网时延空间嵌入算法S-Vivaldi。

本文结构如下：第2节分析TIV影响因特网时延空间模型精度的机理；第3节给出因特网时延空间的修复方法；第4节提出基于空间修复的因特网时延空间嵌入算法S-Vivaldi；第5节使用测量数据集对S-Vivaldi进行验证和讨论；第6节是结束语。

2 TIV对时延空间的影响

先引入相关的定义和定理。

定义1 因特网时延空间：对于一个具有n个节点N={N1, N2, N3,…, Nn}的网络，任一节点Ni到网络中所有节点的时延组成一个n维距离向量di=(di1, di2,…, din)，将所有节点的距离向量所构成的空间D={ d1, d2,…, dn}称为网络时延空间。相应地，由因特网某个节点集合的距离向量所构成的空间称为因特网时延空间。

定义2 度量空间：设X是某个集合，δ:X×X→R+是一个二元映射，并且∀x, y, z∈X满足

非负性：δ(x, y)＞0⇔x≠y

对称性：δ(x, y)=δ(y, x)

三角形不等式：

δ(x, y)≤δ(x, z)+δ(z, y)

则称δ是X上的度量(距离)函数，称M( X,δ)为度量空间。特别地，若X为有限集合，则称M( X,δ)为有限度量空间。

定义3 半度量空间：若定义在X上的度量函数δ具有自反性、对称性，但不满足三角形不等式则称M(X,δ)为半度量空间。

由此，可知因特网时延空间是一个半度量空间而非度量空间。

定义4 等距同构：设(X,δ), (X1,δ1) 2个度量空间，如存在映射ψ：X→X1，满足：1) ψ满射；2)δ(x,y)=δ1(ψ(x), ψ(y)) (x, y∈X)则称(X,δ)，(X1,δ1)是等距同构的。

因特网时延空间建模是为了建立数学模型以描述因特网时延空间的拓扑结构，进而使用度量公式计算和预测任意2个节点间的时延，即寻找因特网时延空间的等距同构空间。具体说，就是构造一个网络节点到m维向量的映射f:N→Rm，将具有n个网络节点的网络N={N1, N2, N3,…, Nn}映射为m维几何空间中的n个坐标点H={H1, H2, H3,…, HN}，同时使得坐标点之间的距离与实际网络测量得到的时延误差值最小，如式(1)所示。其中，ξ表示嵌入误差，ijd表示实测时延，表示预测时延。

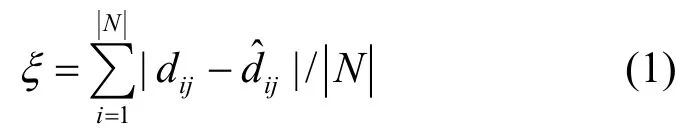
定理1 任意一个具有n个节点的有限度量空间M( X,δ)均可以以O(logn)的扭曲度嵌入到一个O(logn)维欧氏空间中[9]。

定理1说明如果一个空间可以以较小的误差嵌入到欧氏空间中，则必须要求原始空间为度量空间。然而，由于因特网时延空间是一个半度量空间，存在大量TIV现象，使得因特网时延空间D不存在到欧氏空间的同构映射，从而引入了较大的嵌入误差。下面使用经典的空间嵌入算法MDS来分析TIV对因特网时延空间嵌入误差的影响。

MDS算法分为3步：1) 获得节点间平方距离矩阵D(2)=[]；2) 对D(2)进行中心化，BD=-(1/2)JD(2)J，其中，J=I-n-1E，其中，I为单位矩阵，E为全为1的矩阵；3) BD分解得BD=Q∧QT，其中，Q为BD分解后的奇异向量，∧=[λi]为特征值的降序排列，选取其中的正特征值∧+，则Y=Q∧为各个节点的坐标。由此可见，其中的负特征值∧-引入的误差为

此时，可以根据嵌入误差e是否小于预期的阈值来选择嵌入维数r。如果D来自于一个r维欧氏空间Er(r＜＜n)，则BD为一个半正定矩阵，∧中不存在负特征值且其前r个特征值为正。此时，若嵌入维数为大于等于r，可以无误差地进行嵌入。然而，由于因特网时延空间中TIV的存在，则BD的特征值集合∧中存在小于0的特征值。图1是采用MDS算法对因特网时延数据集Harvard、InetDim（参见5.1节的相关解释）和欧氏空间数据集分解后获得的特征值归一化结果，图中给出了其前30个特征值的情况。Harvard和InetDim 2个因特网时延数据集分解后都存在负特征值，而来自于5维欧氏空间的数据集分解后获得的特征值均为非负值。

图1 MDS算法分解的谱分量

可见，TIV是导致嵌入误差的一个重要因素。然而，以往的网络坐标系统无论是采用具有一定曲率的空间进行嵌入[10]，还是通过将时延空间划分为较小的子空间，都无法消除TIV引入的误差。为了解决由TIV产生的较大因特网时延空间嵌入误差的问题，本文提出一种基于空间修复的因特网时延空间嵌入算法。

3 因特网时延空间修复

基于空间修复的因特网时延空间嵌入算法基本思想如下:设存在一个同构的映射T:D→D'，即将因特网时延空间D修复为一个度量空间D'，并假设D'存在一个与其等距同构的k(k＜＜n)维欧氏空间Rk。若D'嵌入到Rk后的坐标集合为C，这样就可以建立从网络节点N到坐标空间C的一个映射。当需要估计或者预测网络中任意2个节点间的距离时，可以通过逆变换计算出嵌入后节点间的距离矩阵Dˆ（其中，δ为度量函数）。算法的关键在于能否找到一个映射T，且T存在一个单射的逆变换T '。

空间修复技术是一种将非度量空间变换为度量空间的映射T，通过空间修复可以获得与原始空间同构且不存在TIV现象的映射空间。将半度量空间变换为度量空间主要有2种空间修复技术：最短路法和指数修复法[11]。最短路法就是通过寻找任意2点之间的最短距离作为修复后2点间距离，该最短距离可用式(3)定义，最短距离可以使用Dijkstra等算法来计算，其中，x、y表示2个节点，ni表示从x到y路径上的节点，Dis(ni,ni+1)表示节点间的距离。然而这种变换却无法确定从修复后的距离矩阵D'到原始距离矩阵D的逆变换。

指数修复法则不存在无法进行逆变换的问题，进行逆变换时只需要对修复后矩阵的元素进行逆指数变换即可。对于一个距离矩阵而言，若Dis(x, y)代表节点x和y之间的距离，当节点之间距离出现违反三角形不等式约束情况时，若进行变换Dis′( x, y):=Dis( x, y)1/ω，即可消除这些节点间的TIV问题，其中，修复系数为ω=maxx,y,z∈Nlb(Dis(x,z)/Dis(x,y))。这是由于对于任何距离矩阵，当ω→∞时，∀x∀ y( x≠y→Dis( x, y)=1)，此时肯定不存在TIV现象。这种变换的最大优点是能在满足保序性的前提下实现空间修复，即节点在原始空间中的距离临近度关系不因变换而改变；缺点是当修复系数ω取值过大时，会使数据丧失一些原有属性，如聚簇特性。

2.2.3 多水塘技术 尹澄清首先提出多水塘系统的概念，主要内容包括水塘和滞留池[13]。修建暴雨滞留池是控制农业面源污染的重要方法[14]，也是欧美国家中污染控制的有效方法。多水塘系统能截留94%以上农业中的氮、磷污染负荷[15]。尹澄清等学者发现，人工多水塘系统具有很强的截留面源污染物的能力，能截留大部分无机态铵态氮和正磷酸根态磷。

下面通过一个简单示例阐述如何通过指数变换将距离本来不满足三角形不等式约束的网络节点无误差地嵌入到二维欧氏空间中。图2(a)中由于节点间距离违反三角形不等式约束Dis(B,C)＞Dis(A, B)+Dis(A,C)，因此在嵌入(如使用Vivaldi算法)到图2(b)二维欧氏空间中时始终存在误差，其误差为在图2(c)中，当修复系数ω=2时即可使得节点满足三角形不等式，从而使节点无误差地嵌入到图2(d)所示二维欧氏空间中。由此可见，在选择合适修复系数的前提下，空间修复能够有效地消除TIV现象对空间嵌入的影响，进而提高距离预测精度。

图2 基于空间修复实现无误差空间嵌入

利用指数变换的空间修复技术，分别采用不同的修复系数对Harvard数据集和InetDim数据集进行了空间修复，结果如表1所示。结果表明，随着修复系数ω增大2个数据集中的TIV比例都明显地减小。这说明空间修复技术能够有效减少因特网时延中的TIV现象，从而减轻TIV对距离预测精度的影响。

表1 采用不同修复系数后的TIV比例

4 基于空间修复的时延空间嵌入算法

将一个空间坐标嵌入到某目标空间的方法有多种，常用的算法有半定规划 (SDP, semi-definite programming) 方法、MDS、单纯型下降 (DHS,down-hill simplex) 算法、Lipschit嵌入算法、Vivaldi[12]以及BBS[10]算法等。本文在最常用的网络坐标系统嵌入算法 Vivaldi基础之上，提出一种基于空间修复的因特网时延空间嵌入算法 S-Vivaldi(scaling-Vivaldi)。

Dabek认为，节点坐标嵌入的过程本质上就是最小化全局误差的过程，而这一全局最小化过程与物理上通过调整弹簧端点位置最小化弹簧的弹性势能非常类似[12]。Vivaldi算法将距离预测误差之和最小化问题类比为弹簧弹性势能最小化问题来进行求解。节点在加入系统前随机测量到系统中一组节点的距离，然后根据测量结果确定自己的初始坐标值。每个节点 Ni与其邻居节点 Nj都通过一个虚拟弹簧相连，弹簧在弹性势能的作用下伸长或压缩，最终弹簧在系统预测误差最小时达到一个平衡状态，此时节点的坐标即为最优嵌入坐标。S-Vivaldi的基本思路是在进行节点嵌入前，首先对因特网时延空间 D进行空间修复，然后对修复后的空间 D'采用Vivaldi算法进行嵌入。

S-Vivaldi算法仅在嵌入之前引入因特网时延空间的指数变换，其复杂度与 Vivaldi的复杂度相同，为O(r(L2+LH))。其中，L为基准节点数目，H为网络中节点总数，r为迭代的次数。

算法1 S-Vivaldi

输入：D //距离矩阵

5 算法评价

5.1 数据集

获得用于研究时延空间嵌入和时延空间性质的数据集大致有2种方法：一是直接测量，二是间接估计。采用直接测量的方式，需要部署大量的测量点，测量点间通过ping或traceroute等方法来测量往返时延。用这种方式获得的数据集最接近真实情况，但需要借助分布式测量平台（如PlanetLab、DIMES等）的支持。由于这些测量平台部署的测量点数目有限，获得的数据集规模较小。采用间接估计的方式不需要部署测量点，而是通过某种机制来估计2个节点间的时延。例如测量工具 King，就是通过测量靠近2个 IP地址的DNS服务器间的时延来估计IP地址对间的时延。测量主机可以位于网络的任何位置，而与被测对象的位置无关，但测量数据与真实情况存在一定差异。利用间接测量的方法往往可以获得较大规模的数据集。

本文使用了通过直接测量获取的Harvard数据集和间接测量获取的 InetDim数据来分别验证S-Vivaldi算法，其相关信息见表2。

表2 时延数据集

5.2 S-Vivaldi的嵌入误差

因特网时延空间嵌入算法的精确度是通过嵌入误差来度量的，误差越小则说明算法的精度越高，反之则说明精度越低。嵌入误差定义为

其中，dij表示节点i与节点j之间的RTT实测值，dij表示算法的预测值。

图3是在2个数据集上，采用S-Vivaldi算法和Vivaldi算法实验效果的对比。在实验中，设置的嵌入数为10，邻居数目25，迭代次数为105轮。S-Vivaldi-middle是S-Vivaldi算法的中间结果，即修复矩阵 D'在 Vivaldi算法下的嵌入误差。将 D'进行反变换则得到S-Vivaldi曲线，可以看出这时误差会放大。比较Vivaldi与S-Vivaldi曲线，发现在数据集Harvard上误差较小时，Vivaldi算法优于 S-Vivaldi算法，而当误差大于 0.3以后，S-Vivaldi 的精度大于 Vivaldi算法的精度；而在数据集 InetDim上，S-Vivaldi的精度一直优于Vivaldi算法。在Harvard数据集上，当误差为0.5时，S-Vivaldi算法精度高于Vivaldi算法精度约7%；在 InetDim数据集上，当误差为 0.4时，S-Vivaldi算法精度高于 Vivaldi算法精度约20%。造成这种预测结果差异的原因是Harvard数据中存在大量未知数据，不响应节点间的时延设置为-1，对嵌入结果产生了负面影响，而在数据集 InetDim不响应节点相对较少，进一步分析见5.4节。

5.3 算法参数影响

下面考察嵌入维数对于 S-Vivaldi算法精度的影响。图4比较了S-Vivaldi算法在2个数据上选择不同嵌入维数时的精度，可以看到随着嵌入维数增加则误差随之减小。但当嵌入维数大于 10时，嵌入误差减小的不是十分明显，因而选择嵌入维数10较为合适。

图3 S-Vivaldi与Vivaldi算法在Harvard数据集上的嵌入误差

下面分析 S-Vivaldi算法在不同修复系数(ω)下的嵌入误差。在实验中，为ω设置了许多不同的取值，为了能更加明显地显示S-Vivaldi算法在不同修复系数下的变化趋势，仅列出了4组代表性的数据。图 5是 Harvard数据集在 4个不同修复系数时S-Vivaldi的嵌入误差，结果表明嵌入误差随着ω增大而增大。这是因为当ω→∞时，所有节点间修复后的距离将都为1，成为一个N维的超立方体，无法保持原有距离矩阵中的信息。因此，修复系数一般不宜过大，实验证明当修复系数设为2时能获得较好性能。

图4 不同嵌入维数下的嵌入误差

图5 在不同的修复系数下S-Vivaldi的嵌入误差

5.4 误差分析

因特网时延空间的低维特性是保证嵌入精度的基本前提[14]。实际上空间修复技术仅能消除时延空间中的 TIV，并不能保证修复后的时延矩阵 D'保持原有时延空间D的维数特征。因而采用主成分分析 (PCA, principal component analysis) 法来观察2个数据集修复前后的维数特征。设(λ1, λ2, …, λN)为用PCA算法所求得的时延矩阵D的特征值的降序排列，则前n个主轴的累积贡献率为

在图 6中，直方图表示每一个维度的单独贡献率，曲线表示前几维的累积贡献率。从图中可以看出2个数据集修复前后的维数特征变化是相反的。Harvard数据集修复前，前10维的累积贡献率几乎达到100%，且前5维的单独贡献率较大；而修复后前10维的累积贡献率明显不足100%，且前5维的单独贡献率也没有以前明显。因此，导致了修复后S-Vivaldi在嵌入误差较小时，不如Vivaldi算法精度高。InetDim数据集修复前后变化却是相反的，因此S-Vivaldi的精度一直高于 Vivaldi。从总体上看，Harvard数据集修复前后前几维贡献率都高于InetDim数据集，因而2个算法在Harvard数据集上精度都高于在InetDim上的嵌入结果。这表明数据集修复前后维数的变化会影响S-Vivaldi算法的精度。

下面分析导致2个数据维数特征变化的原因。通过统计，Harvard数据集和InetDim数据集中的不响应数据分别占所在数据集的3.5%和0.1%，虽然两者的比例都不高，但是前者却是后者的35倍。下面分析不响应数据如何影响数据集的特征值分布规律。设节点间的真实时延矩阵为D，而测得数据集为D', B为不响应节点间的时延矩阵，则D'=D-B。若D、D'特征值分别为(λ1, λ2,…, λN)、(λ'1, λ'2,…, λ'N)，根据矩阵的扰动理论[15]，损失的特征值为

由于

因此当||B||2越小时，则|λi-λ'i|越小，变换后损失的特征值信息越少。由于不响应节点的时延矩阵B中节点较少，低维特征明显，特征值主要集中在前几维，从而导致测量数据集的前几维特征值损失较大，累积贡献率下降，出现维数增加。要减小||B||2的值，就要减少测量中的不响应节点。

图6 数据集修复前后的维数特征

在部署S-Vivaldi系统时，要减少测量的不响应节点，可以通过以下2种措施来实现：一是S-Vivaldi系统不允许加入不响应的节点，二是通过引入如Htrae系统中基于地理信息的时延估计方法来对系统进行初始化[16]。

6 结束语

大量网络测量证实了TIV在因特网时延空间中广泛存在，它严重地影响因特网时延空间模型和网络坐标系的精度。目前的研究通过选择带有一定曲率的空间进行嵌入或是将因特网时延空间划分为不同粒度的子空间，都无法解决TIV引入的嵌入误差。由此，本文提出了基于空间修复的因特网时延嵌入算法S-Vivaldi，通过引入指数变换来对因特网时延空间进行修复，大大减少了修复后因特网时延空间的TIV比例，并使用矩阵扰动理论分析了在不同数据集上嵌入误差的原因，使得S-Vivaldi算法更易部署使用。实验分析也验证了S-Vivaldi算法的可行性，该方法同样适用于先前提出的层次化网络坐标系统[2,7,17]。下一步将在因特网中加以部署应用，并做进一步改进。

[1] WANG G, ZHANG B, NG T S E. Towards network triangle inequality violation aware distributed systems[A]. Proceedings of IMC2007[C]. San Diego, CA, USA, 2007. 175-188.

[2] MOHAMED A K, BAMBA G, FRANCOIS C, et al. Towards a two-tier internet coordinate system to mitigate the impact of triangle inequality violations[A]. Proceedings of IFIP Networking Singapore[C]. 2008.397-408.

[3] ZHENG H, LUA E K, PIAS M, et al. Internet routing policies and round-trip-times[A]. Proceedings of PAM[C]. Boston, USA, 2005. 236-250.

[4] LEE S, ZHANG Z L, SAHU S, et al. On suitability of euclidean embedding for host-based network coordinate systems[J]. IEEE/ACM Transactions on Networking, 2010, 18(1): 27-40.

[5] WANG G, ZHANG B, NG T S E. Towards network triangle inequality violation aware distributed systems[A]. Proceedings of IMC2007[C]. San Diego, CA, USA, 2007.175-188.

[6] ZHANG B, NG T S E, NANDI A, et al. Measurement-based analysis,modeling, and synthesis of the internet delay space[A]. Proceedings of IMC2006[C]. Rio de Janeiro, Brazil, 2006.

[7] ZHU Y, CHEN Y, ZHANG Z, et al. Taming the triangle inequality violations with network coordinate system on real internet[A]. Pro-ceedings of ReArch'10 Conjunction with CoNEXT'10[C]. Philadelphia,USA, 2010.

[8] LIAO Y, MOHAMED A, GUEYE K B, et al. Work in Progress:Detecting Triangle Inequality Violations in Internet Coordinate Systems by Supervised Learning[R]. Technical Rseport, 2009.

[9] MATOUSEK J. Lectures on Discrete Geometry[M]. New York,Springer-Verlag, 2002.212.

[10] SHAVITT Y, TANKEL T. Big-Bang simulation for embedding network distances in euclidean space[J]. IEEE/ACM Transactions on Networking, 2004, 12 (6): 993-1006.

[11] CLARKSON K. Nearest-Neighbor Searching and Metric Space Dimensions. Nearest-Neighbor Methods for Learning and Vision: Theory and Practice[M]. Cambridge, Massachusetts, USA: MIT Press,2006.

[12] DABEK F, COX R, KAASHOEK F, et al. Vivaldi: a decentralized network coordinate system[A]. Proceedings of SIGCOMM2004[C].Portland, OR, USA, 2004.15-26.

[13] NC research group at Harvard[EB/OL]. http://www.eecs.harvard.edu/syrah/nc, 2008.

[14] ABRAHAO B, KLEINBERG R. On the Internet delay space dimensionality[A]. Proceedings of IMC[C]. Vouliagmeni, Greece, 2008. 157-168.

[15] 戴华. 矩阵论[M]. 北京:科学出版社, 2005. 189-198.DAI H. Theory of Matrices[M]. Beijing: Science Press, 2005. 189-198.

[16] AGARWAL S, LORCH J R. Matchmaking for online games and other latency-sensitive P2P systems[A]. Proceedings of SIGCOMM2009[C].Barcelona, Spain, 2009.315-326.

[17] ZHANG R, HU Y, LIN X, et al. A hierarchical approach to internet distance prediction[A]. Proceedings of ICDS2006[C]. Washington,DC, USA, 2006.73-80.