胡 钢，吉晓民，沈晓芹，宋伟杰

（1. 西安理工大学理学院，陕西 西安 710054; 2. 西安理工大学机械与精密仪器工程学院，陕西 西安 710048; 3. 西北工业大学理学院，陕西 西安 710072）

CE-Bézier曲面光滑拼接的研究与实现

胡 钢1,2，吉晓民2，沈晓芹1，宋伟杰3

（1. 西安理工大学理学院，陕西 西安 710054; 2. 西安理工大学机械与精密仪器工程学院，陕西 西安 710048; 3. 西北工业大学理学院，陕西 西安 710072）

针对CE-Bézier曲面造型中复杂曲面难以用单一曲面来表示的问题，通过分析CE-Bézier曲线的唯一性，提出了一种新的CE-Bézier曲面的光滑拼接技术。首先，在分析第1类CE-Bézier曲线基函数及其端点性质的基础上，对第1类CE-Bézier曲线的唯一性进行了研究，得出了对于同一条第1类CE-Bézier曲线可以有很多组不相同的控制顶点和形状参数与之对应的结论；其次，利用该结论进一步给出了两相邻第1类CE-Bézier曲面片间 G1光滑拼接的一般几何条件，并通过合理地选取形状参数，进一步简化了该曲面的 G1拼接条件；最后，给出了第1类CE-Bézier曲面光滑拼接的几何造型实例。实例结果表明，该方法简单、直观、易实现，有效地增强了CE-Bézier方法表达复杂曲线曲面的能力，可广泛地应用于工程复杂曲面的造型系统中。

CE-Bézier曲线；CE-Bézier曲面；形状参数；光滑拼接；唯一性分析

随着几何造型工业的快速发展，传统Bézier和有理 Bézier方法已难以满足曲线曲面几何造型中的各种需求[1]。为了保留原有Bézier方法的优点，同时增加曲线曲面的形状可调性和逼近性，人们提出了一些推广的带形状参数的Bézier曲线曲面，如C-Bézier[2]、q-Bézier[3]、T-Bézier[4]、带单参数的Bézier[5]、拟三次Bézier[6]、H-Bézier[7]以及CE-Bézier曲线曲面[8]等。其中，CE-Bézier曲线曲面不仅是文献[5-6]中曲线曲面的进一步推广，而且具有类似 Bézier曲线曲面的端点性质、凸包性、变差缩减性以及仿射不变性等诸多几何性质，其形状可调性也要优于其他曲线曲面[2-7]。此外，由于它是代数多项式曲线曲面，所以其实际计算复杂度要远低于非代数多项式曲线曲面，如C-Bézier、T-Bézier及H-Bézier曲线曲面等。

为了进一步增强CE-Bézier曲线曲面表达复杂曲线曲面的造型能力，文献[9]研究了第 1类CE-Bézier曲线曲面的光滑拼接问题，但所得的曲面拼接条件不仅复杂、含有基函数、几何意义也不明确，而且还无法应用于实际复杂曲面的构造。为此，本文从第1类CE-Bézier曲线自身性质出发，分析了该曲线的唯一性，并利用所得结论给出了第1类CE-Bézier曲面光滑拼接的一般条件。所得条件不仅几何意义明显、结构简单、便于实际操作，而且为第1类CE-Bézier曲面连续阶的判断、光滑拼接曲面的构造以及计算机的实现都带来了很大的方便。

1 第1类CE-Bézier曲线的定义

定义1 给定4个控制顶点 P∈ Rn(n =2,3;ii =0,1,2,3)，对 t∈ [0,1]定义曲线

称式（1）所定义的三次多项式曲线为带形状参数α ,γ的第1类三次扩展Bézier曲线，简称第1类CE-Bézier曲线[8]。式中，三次多项式基函数bi,3(t)(i=0,1,2,3)定义如下

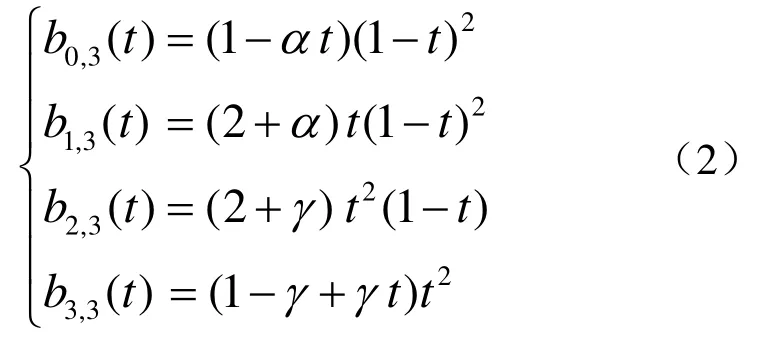
式中， ]1,2[, -∈γα 。显然，当 1==γα 时，曲线式（1）便退化为传统三次Bézier曲线。由式（1）不难推出第1类CE-Bézier曲线具有对称性、凸包性、几何不变性、仿射不变性以及如下端点性质：

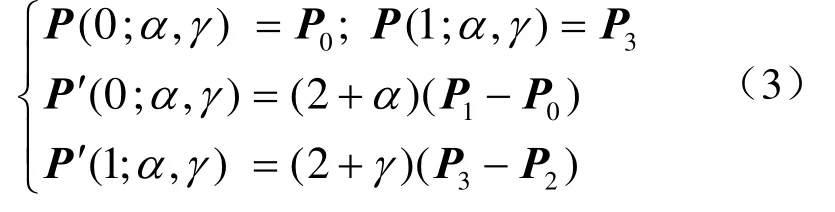
2 第1类CE-Bézier曲线的唯一性分析

对于传统三次Bézier曲线，若给定4个具体的控制顶点，则有唯一的一条三次Bézier曲线与之对应；反之，对于一条具体的三次Bézier曲线同样有唯一的4个控制顶点与之对应。那么，此结论对于第 1类 CE-Bézier曲线是否同样成立呢？下面给出具体的分析，不妨设 P (t ;α1,γ1)和Q (t ;α2,γ2)为由式（1）所定义的两条第 1类CE-Bézier曲线，其控制顶点分别为 P0,P1,P2,P3和Q0,Q1,Q2,Q3。

定理 1 两条曲线 P (t ;α1,γ1)和 Q(t;α2, γ2)表示同一条多项式曲线的充分必要条件是它们的控制顶点和形状参数满足如下条件

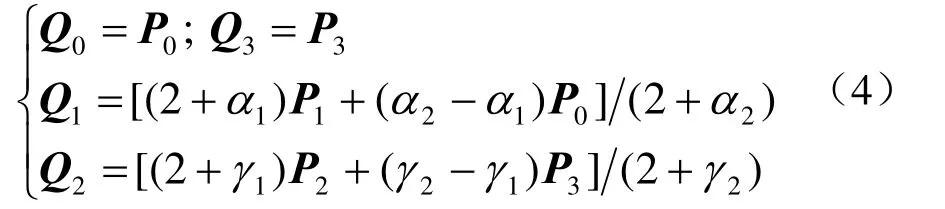
同时成立。

证明 若两条 CE-Bézier曲线 P(t ;α1,γ1)和Q(t;α2,γ2)表示同一条多项式曲线，即

根据曲线的端点性质和对比式（5）中两边多项式曲线的各幂项系数，稍加整理即可将式（5）等价为

最后将式（6）中前3个等式分别代入第4、5个等式中，稍加整理即可得式（4）成立。 证毕。

定理 1表明，对于一条具体的第 1类CE-Bézier曲线，则可以有很多组不相同的控制顶点和形状参数与之对应，即在不改变第 1类CE-Bézier曲线形状的情况下，可以按式（4）中的条件来修改该曲线的控制顶点和形状参数。

图1给出了不同控制顶点和形状参数表示同一条第1类CE-Bézier曲线的实例。其中，第1类CE-Bézier曲线的初始控制顶点P0, P1, P2, P3坐标取为(0,0)、(0.3, 0.7)、(0.8, 0.8)和(1,0)，且原始形状参数α和γ都取值为0。如图1所示，若

图1 不同控制顶点和形状参数表示同一条CE-Bézier曲线的实例

1） P0, P3位置固定不变；

2） 当α增大（或减小）时，点P1应按直线的方向靠近（或远离）点P0，且具体偏移位置可由式（4）中的第3个等式计算出；

3） 当γ增大（或减小）时，点P2应按直线的方向靠近（或远离）点P3，且具体偏移位置可由式（4）中的第4个等式计算出。

3 第1类CE-Bézier曲面的光滑拼接

3.1 第1类CE-Bézier曲面的定义

定义 2 若给定4×4个控制网格顶点Pi,j(i, j=0,1,2,3)，将与第1类CE-Bézier曲线对应的张量积曲面

称为[0,1]×[0,1]上的第1类CE-Bézier曲面[9]。式中，-2 ≤α ,γ,β,ω ≤1 ，bi,3(u ),bj,3(v)为式（2）所定义的基函数。显然当所有参数都为1时，第1类CE-Bézier曲面便退化为传统的双三次Bézier要保持第1类CE-Bézier曲线的形状和位置不变，则须满足：曲面，且可灵活地改变形状参数来调整曲面的形状。

3.2 第1类CE-Bézier曲面的G1光滑拼接

在实际应用中，曲面间通常要达到G1连续，即2张曲面在公共连接线处有公共的切平面或公共的曲面法线[10-12]。设有2张第1类CE-Bézier曲面 P(u,v;α1,γ1,β1,ω1)和Q(u,v;α2, γ2, β2,ω2)，其控制网格顶点分别为 pi,j和 qi,j(i, j=0, 1,2,3)，由于CE-Bézier曲面存在方向性，所以2张曲面片间的拼接存在以下3种形式：

1） u向与u向拼接；

2） u向与v向拼接；

3） v向与v向拼接。

定理 2 若两相邻曲线片 P(u,v;α1,γ1,β1, ω1)和 Q (u,v;α2,γ2,β2,ω2)满足如下条件

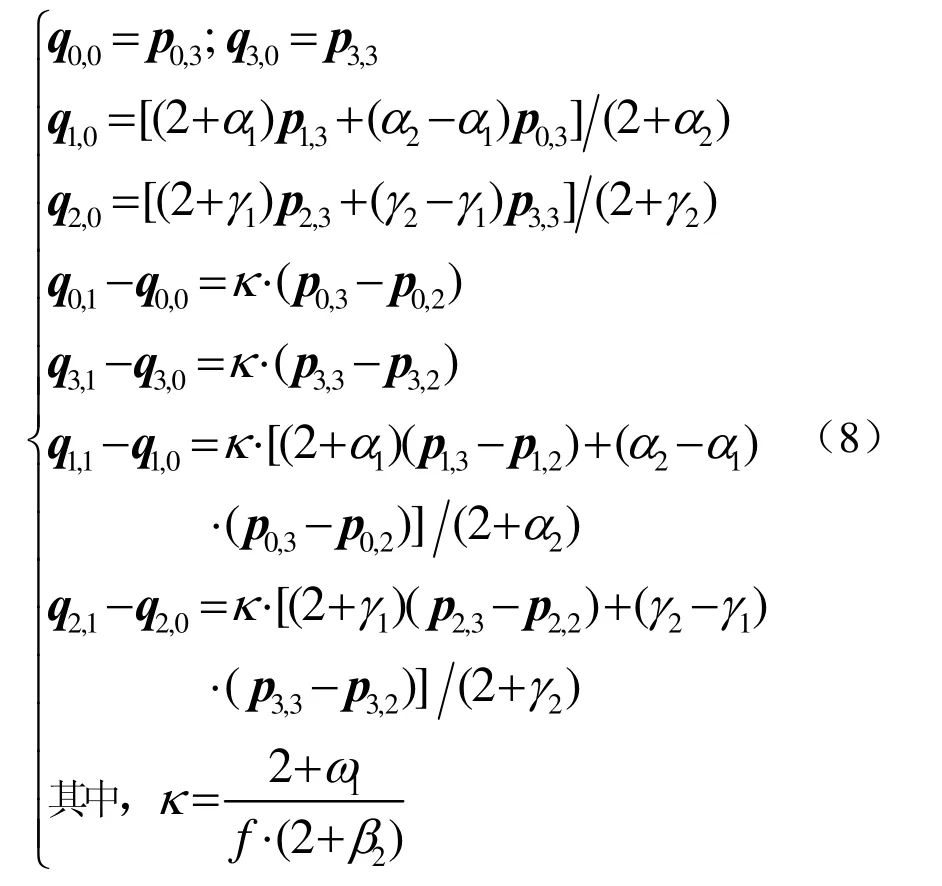
同时成立，则两曲面片 P (u ,v)和 Q (u ,v)在公共边界处达到u向与u向G1光滑拼接。

证明 2张曲面片要达到u向与u向G1连续，首先要求它们在u向处有一公共边界，即

P(u,1;α1,γ1,β1,ω1)=Q(u,0;α2,γ2,β2,ω2)由曲面的定义可将上式化简为

再根据定理 1中的结论，可将式（9）进一步整理为

其次，要求2张第1类CE-Bézier曲面片在拼接边界处有公共的切平面，即两曲面片在边界上的法矢方向是连续的。所以，数学上应满足[10-12]

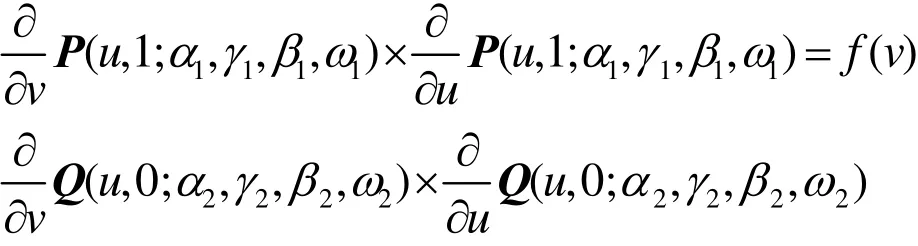
且实际应用中常采用Faux方法[12]可将上式简化为

式中，f为大于0的实常数。式（11）的几何意义为两曲面拼接时跨界切矢的方向是连续的。计算曲面片的跨界切矢，并代入式（11）得

再利用定理1中的结论，可将式（12）进一步整理为

综上所述，式（10）和式（13）便构成了2张第1类CE-Bézier曲面片u向与u向G1光滑拼接的一般条件，从而定理 2得证。此外，若令α1= α2,γ1=γ2,ω1= β2，则式（10）和式（13）可进一步简化为

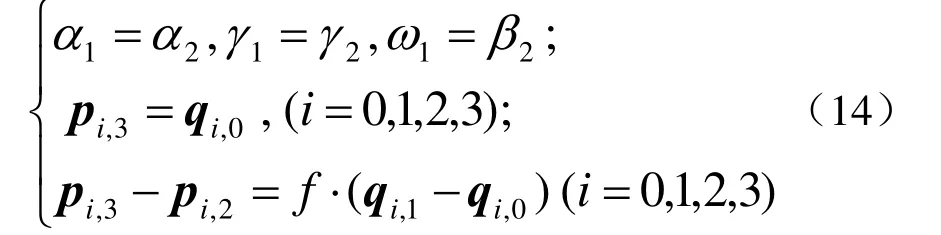
因此，式（14）便构成了2张第1类CE-Bézier曲面片u向与u向G1光滑拼接的一个简洁充分条件，其几何意义为：若满足α1=α2,γ1=γ2,ω1=β2，则G1连续的2张曲面片具有相同的 4 个控制顶点，且pi,2,pi,3(= qi,0),qi,1共线并有序排列。与u向与u向的拼接类似，对于2张第1类CE-Bézier曲面片u向与v向（或v向与v向）的拼接，同理可得如下的结论。

定理 3 若两相邻曲线片 P(u,v;α1,γ1,β1, ω1)和Q(u,v;α2,γ2,β2,ω2)满足如下条件

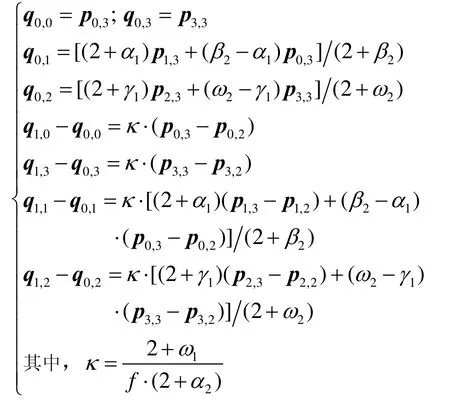
同时成立，则两曲面片 P (u ,v)和 Q (u ,v)在公共边界处达到u向与v向G1光滑拼接。

定理 4 若两相邻曲线片 P(u,v;α1,γ1, β1, ω1) 和 Q (u ,v;α2,γ2,β2,ω2)满足如下条件

同时成立，则两曲面片 P (u,v)和 Q (u ,v)在公共边界处达到v向与v向G1光滑拼接。

3.3 曲面拼接的步骤与实例

这里以第1类CE-Bézier曲面片u向与u向拼接为例，对于曲面片u向与v向（或v向与v向）的拼接可类似讨论。根据定理2中的结论可知，实现2张第1类CE-Bézier曲面片u向与u向G1光滑拼接的基本步骤为：

1） 先给定初始曲面片P(u ,v;α1,γ1,β1,ω1)的控制网格顶点 pi,j以及参数α1, γ1,β1,ω1。

2） 令 q0,0=p0,3; q3,0=p3,3，再自由给定参数α2,γ2，并由式（8）中的第3个和第4个等式计算出 q1,0,q2,0，从而使得曲面片P(u,v;α1,γ1,β1,ω1)和Q(u,v;α2,γ2,β2,ω2)具有一条公共边界。

3） 自由给定常数f和参数 β2，在步骤2）的基础上再根据式（8）中的第5个至第8个等式分别计算出曲面 Q (u ,v;α2,γ2,β2,ω2)的一排控制网格顶点 q0,1,q1,1,q2,1,q3,1。

4） 最后，自由给定曲面 Q(u,v;α2,γ2,β2, ω2)的两排控制网格顶点 qi,2和 qi,3(i =0,1,2,3)以及参数ω2，即可实现2张曲面片间的G1光滑拼接。

显然，反复利用上述的拼接步骤，还可实现多片（2片以上）第1类CE-Bézier曲面间的G1光滑拼接。图2给出了2张第1类CE-Bézier曲面片（用实、虚网格曲面区分）u向与 u向 G1光滑拼接的实例。其中，图2(a)中2张曲面片的控制网格顶点和形状参数按定理2中的条件来取值，而图2(c)与图2(b)中的曲面具有相同的控制网格顶点。从拼接结果来看，2张曲面片在公共边界处具有了公共的切平面，且光滑拼接的效果较好。此外，在实际工程应用中还可根据需要改变形状参数，来灵活调整拼接后曲面的形状，同时还不会影响曲面拼接的光滑程度。

图2 第1类CE-Bézier曲面的G1拼接

图3给出了相邻4张第1类CE-Bézier曲面片（用实、虚网格曲面区分）间 G1光滑拼接的实例。从图3中可以看出，四张曲面片在公共边界处过度自然、光滑，达到了较好的拼接效果。

4 结 论

为了解决第1类CE-Bézier曲面造型中复杂曲面的构造问题，对第1类CE-Bézier曲线进行了唯一性分析，得出了对于同一条第 1类CE-Bézier曲线可以有很多组不同的控制顶点和形状参数与之对应的结论；并利用该结论给出了第1类CE-Bézier曲面间G1光滑拼接的一般条件。理论分析和造型实例表明，第1类CE-Bézier曲面不仅具有灵活的逼近方式，而且其拼接条件也具有简单、直观的特点，可以用来生成多种不同的常用曲面，因而在工程曲面构造中有着广泛的应用前景。

[1] Mamar E. Shape preserving alternatives to the rational Bézier model [J]. Computer Aided Geometric Design, 2001, 18(1): 37-60.

[2] Zhang Jiwen. C-curves and surfaces [J]. Graphical Models and Image Processing, 1999, 61(1): 2-15.

[3] Oruc H, Phillips G H. q-Bernstein polynomials and Bézier curves [J]. Journal of Computational and Applied Mathematics, 2003, 151(1): 1-12.

[4] 丁 敏, 汪国昭. 基于三角和代数多项式的T-Bézier曲线[J]. 计算机学报, 2004, 27(8): 1021-1026.

[5] 吴晓勤, 韩旭里. 三次 Bézier曲线的扩展[J]. 工程图学学报, 2005, 26(6): 98-102.

[6] 韩西安, 马逸尘, 黄希利. 拟三次Bézier曲线的形状调整[J]. 西安交通大学学报, 2007, 41(8): 903-906.

[7] 檀结庆, 王 燕, 李志明. 三次 H-Bézier曲线的分割、拼接及其应用[J]. 计算机辅助设计与图形学学报, 2009, 21(5): 584-588.

[8] 秦新强, 胡 钢, 张素霞. 三次Bézier曲线的新扩展及其应用[J]. 计算机工程与应用, 2008, 44(2): 112-115.

[9] Qin Xinqiang, Liu Fei, Hu Gang, et al. The continuity of cubic extension Bézier curves and surfaces [C]// Proceedings of Thirteenth IEEE International Conference on Computer Science and Information Technology. Piscataway, NJ, USA: IEEE Press, 2010: 489-493.

[10] 李 鹏, 李 原, 刘 平, 等. C-B样条曲线及曲面的光滑拼接与应用[J]. 西北工业大学学报, 2007, 25(6): 890-895.

[11] 胡 钢, 秦新强, 韩西安, 等. 拟三次 Bézier曲线曲面的拼接技术[J]. 西安交通大学学报, 2010, 44(11): 46-50.

[12] Farin G. Curves and surfaces for CAGD: a pratical guid fifth edition [M]. San Diego: Academic Press, 2002: 368-376.

Research on the continuity conditions for CE-Bézier surfaces

Hu Gang1,2, Ji Xiaomin2, Shen Xiaoqin1, Song Weijie3
( 1. School of Science, Xi’an University of Technology, Xi’an Shaanxi 710054, China; 2. Faculty of Mechanical and Precision Instrument Engineering, Xi’an University of Technology, Xi’an Shaanxi 710048, China; 3. School of Science, Northwestern Polytechnical University, Xi’an Shaanxi 710072, China )

Focusing on the problem that the engineering complex surfaces can not be described by using a single cubic extension Bézier (CE-Bézier) surfaces with multiple shape parameters, the continuity conditions of CE-Bézier surfaces are proposed. Following the analysis of basis functions and terminal properties, the unique property of CE-Bézier curves is investigated and the corresponding conclusion that a CE-Bézier curve can be defined by many different groups of control points and shape parameters is also obtained. And then, the geometric model of CE-Bézier surfaces is constructed and the condition of G1continuity between two adjacent CE-Bézier surfaces in u and v directions is derived and simplified by choosing the control parameters properly. The modeling examples illustrate that the continuity condition of CE-Bézier surfaces can be widely applied to the complex surfaces modeling system.

CE-Bézier curve; CE-Bézier surface; shape parameter; continuity condition; analysis of unique property

TP 391.4

A

2095-302X (2012)05-0062-06

2010-08-15；定稿日期：2011-01-06

国家自然科学基金资助项目（10926152，11101330）；陕西省自然科学基金资助项目（2011JM1006）；陕西省教育厅基金资助项目（11JK1052）；徐州工程学院青年教师基金资助项目（XKY2007319）

胡 钢（1979-），男，江西高安人，讲师，博士研究生，主要研究方向为计算机辅助几何设计与图形学、图像处理。E-mail：huhui_xauot@163.com