杨玉坤，杨明玉

（1.吉林省电力勘测设计院，长春 130022；2.华北电力大学电力系统保护与动态安全监控教育部重点实验室，保定 071003）

随着电力电子装置在电力系统中的广泛应用以及非线性负荷的日益增多，电力系统中的谐波污染越来越严重和复杂。谐波污染除了与基波成整数倍的谐波外，还存在许多非整数倍的间谐波。间谐波的存在不仅会对电力系统造成更大的危害，更增加了谐波检测的难度。

目前常用的谐波检测分析方法是基于傅里叶变换的算法，但是它们对间谐波的分析存在着频谱泄漏和栅栏效应现象［1］。近年来一些新的方法被用于谐波检测当中，其中现代谱估计方法中的Prony算法由于无需估计样本自相关函数，只需求解两组齐次线性方程和一个线性多项式便可以一次性辨识出信号中各分量的频率、幅值、衰减因子和初相，并具有较高的辨识精度，该算法已在国内外的谐波检测研究中得到充分重视［2～4］。

以往Prony算法的谐波检测研究中，都是依靠滤波或迭代的方法来提高Prony算法的辨识精度，但是它们都是以提升算法的计算量为代价的。而在线的谐波检测要求具有很好的实时性，因此在保证精度的前提下，寻找一种能够减小算法复杂度的方法具有十分重要的意义。另外，Prony算法的辨识精度与其参数选择有很大的关系，而以往的研究中，没有细致地讨论过最优参数的选取问题，对于如何识别由于较高模型阶数引起的虚假频率成分问题，也没有一个可靠的方法。本文就针对该问题进行研究。

1 Prony算法建模与求解的基本思路

Prony算法采用p个指数项的线性组合来拟合等间隔采样数据（本文后面称p为模型的阶数）。设N个采样数据为x（0），x（1），…，x（N－1），则有

定义

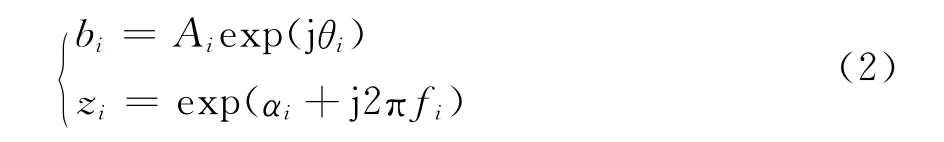
可由欧拉公式得

即只需求解bi和zi即可用p个具有任意幅值Ai、频率fi、相位θi和衰减因子αi的余弦分量来拟合采样数据。式（3）是常系数线性差分方程

的齐次解其特征多项式为

并代入式（4）可得

Prony算法的求解即为求取ai使误差的平方达到最小。将ai代入特征多项式（5）求得zi，再代入由式（1）组成的方程组求得bi，即

最后利用zi和bi的定义式求得p个余弦量的幅值Ai、频率fi、相位θi和衰减因子αi。

2 Prony算法求解方法的改进

对于式（7）中ai的求解，通常的方法是构造误差ε（n）的平方和J（a）为代价函数，即

令

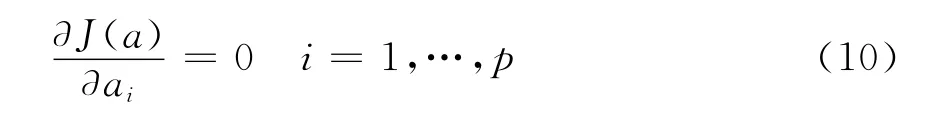
使其达到最小，最后得到方程组［5］为

本文提出的方法是直接令误差ε（n）＝0，则由式（7）可得求解ai的方程组为

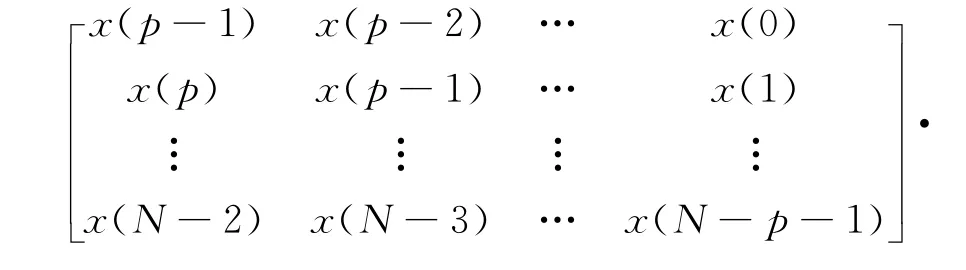
可简写为Ya＝y

对于方程组（12），由于一般取p＜N／2通常为等式个数大于未知数个数的超定方程组。对于求解超定方程组的一般方法有最小二乘法、奇异值分解SVD（singular value decomposition）和正交三角分解QR（quadrature right－triangle）。SVD算法和QR算法由于避免了矩阵的求逆运算，所以较最小二乘法稳定，且有相应的成熟算法，求解速度非常快。文献［7］比较了SVD分解和QR分解算法的浮点运算数量级，当方程组（12）中的Y是一个阶矩阵时，Golub－Reinsch SVD算法的数量级为4mn2＋8n3，而Householder QR算法的仅为2mn2－2n3／3。为了尽量缩短Prony算法在线谐波检测的耗时，本文采用QR分解算法来求解上述超定方程组。

对矩阵Y进行QR分解，就是把Y分解为一个正交矩阵Q和一个上三角矩阵R的乘积形式，即Y＝QR，代入最小二乘解的一般表达式中得

式（13）又可转化为非常容易求解的上三角方程组

综上所述，本文所提出的求解式（7）中ai的方法，在算法复杂度和稳定性方面明显优于传统方法。值得提出的是，对于方程组（8）中bi的求解，也是一个超定方程组，其原始解法是利用式（4）递推出x∧（n），再用最小二乘法求解。应用本文所提出的QR分解算法，先令x∧（n）＝x（n）再去求解，可以进一步减小算法的计算量。

另外，求解ai的方程组（12）和bi的方程组（8）不是一般类型的方程组。如方程组（12）中的Y是各条主对角线上元素皆相同的“Toeplitz矩阵”；方程组（8）中矩阵的每一行依次是极点zi的0，1，2，…，N－1次幂，为“Vandermonde矩阵”。用QR分解这两类矩阵时，都有相应的快速算法［8，9］，这为进一步提高Prony算法的计算效率提供了有力的数学支持。

3 Prony算法的参数选取

3.1 模型阶数的选取

一般情况下，信号中频率成分的个数是未知的且常常含有噪声；选取较大的阶数进行Prony分析时，辨识结果中所增加的余弦分量可被用来拟合信号中的噪声成分，有利于提高算法的性能。但表征噪声的频率分量会干扰真实成分的辨别与提取，过大的模型阶数反而会降低算法的性能。大量实验结果表明，最佳阶数范围和总的采样点个数密切相关，一般为（0.35～0.45）倍的采样点个数N。

模型阶数与采样点数的关系对算法性能的影响可用“方程的时间跨度”的概念来解释（如图1）。观察方程组（12），样本矩阵Y的每一行都是由阶数p个采样点构成，各行所使用的数据在序列上只相差1个数据点，相当于一个子窗口在移动。p越大，每一行所使用的采样点数越多，由这p个采样点覆盖信号的时间越长，越能表达信号的信息；若p过大，由于总的采样点数一定，样本矩阵Y的行数（即等式个数）将很少，超定方程组将趋近于适定方程组甚至欠定方程组，以致降低算法的性能。

图1 方程的时间跨度Fig.1 Time span of the equation

3.2 采样频率的选取

在满足采样定理的前提下，适当增大采样频率可以提高算法的精度。但在时间窗确定的情况下，增大采样频率会导致运算量大幅度上升。一些文献中提出采样频率应取4～10倍信号中的最高频率较为合适［5］。这种方法的可靠性较低，事实上实际需要分析的信号的频率范围是变化的，即使是某一固定的信号，在不同的噪声环境中用相同的采样频率辨识，算法的性能也往往不同。

本文提出一种自适应采样频率的方法：对于方程组（12），在矩阵理论中其最小二乘解为YTY的最小特征值对应的特征向量。设YTY满足

式中：λi为特征值；xi和wi是λi的右特征向量和左特征向量，它们的二范数均为1。假如YTY受到了一个扰动变为YTY＋εF，其中ε为二范数为1的矩阵F的系数，则式（15）和（16）将变为

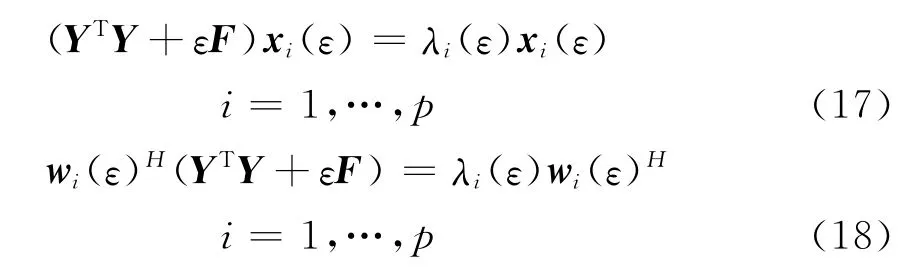
此时的最小特征值对应的特征向量设为xmin.index（ε），它和未经扰动时的最小特征值对应的特征向量xmin.index之间的关系［10］为

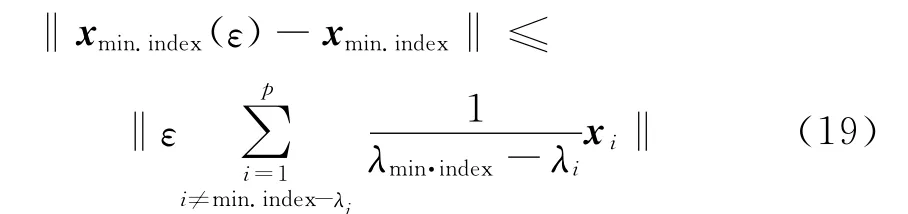
即YTY受到了一个扰动后方程组的解和未经扰动时的解的差之间存在着一个最大值，在不同的采样频率时该最大值是不同的。那么找到了此最大值最小时对应的采样频率，也就找到了受扰动影响最小的采样频率，定义灵敏度公式为

式（20）可以作为各个采样频率的评价指标。在进行Prony分析之前，先以较高的采样频率采集数据，再进行各倍率的抽取以得出各采样频率时的数据，分别用这些数据形成方程组（12），再利用式（20）进行灵敏度计算，最后用灵敏度最小时的方程组求取Prony算法中的ai。

3.3 时间窗的选取

在噪声水平和采样频率确定的情况下，时间窗越长估计的精度越高，但过长则可能无法辨识出衰减快的分量同时会增加计算量。大量的实验证明，时间窗长度应为信号中最低频率分量的1～2个周期。考虑到谐波中存在频率低于50 Hz的分量的情况，时间窗取为80 ms能够满足绝大多数谐波检测的需要。

4 真实频率成分的提取方法

根据上文所述，为了提高算法的精度应选取较大的模型阶数，但分析结果中会出现一些信号中原本不存在的、表征噪声的频率分量，它们干扰了真实成分的辨别与提取。本文提出一种基于能量的提取方法，这种方法可靠且计算量十分小。

由于虚假成分是被用来拟合信号中的噪声成分，所以其幅值都不会太大，或者呈现快速衰减的规律。所定义的能量要同时反映这两个参数，既要设法突出幅值大的或者（和）衰减慢的频率分量，

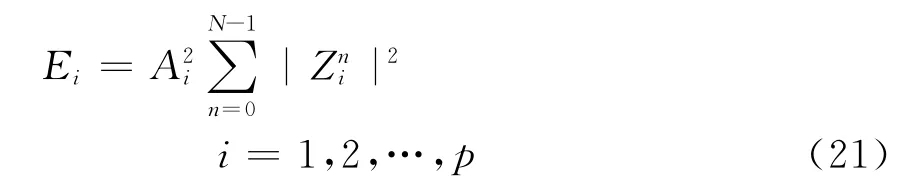
式中：Ei为各频率分量的能量；Ai为各频率分量的幅值；为代表各频率分量的极点的n次幂；N为采样点数；p为模型阶数。

本文定义该能量表达式的理由如下：

①反映了各频率分量幅值和衰减的大小，因为由z的定义式可知，z的模值越大其衰减因子越小对应衰减越慢；

②所需的计算量十分小，因为zni的计算已在Prony算法的第二个线性方程组（8）中计算完毕，整个能量计算只需要少量的乘法和加法计算。

真实频率成分和噪声成分在本文所定义的能量上具有明显的差异：真实频率成分的能量要远大于噪声成分的能量。将各成分按能量从大到小排序，当能量迅速地减小时可认为后面的是虚假频率分量。又要考虑计算量的大小以适合在线计算快速性需要。本文定义各频率分量能量的表达式为

5 算例分析

为了阐述本文所提出的Prony算法完整的求解过程，说明其在电力系统谐波参数辨识中应用的可行性，本文采用文献［3］中没有安装补偿装置的电弧炉电流波形来进行分析。信号是由基波（50 Hz，100 A，相位30°）、高次谐波（125 Hz，75 A，相位－60°）和间谐波（25 Hz，65 A，相位90°）组成，另外还加有信噪比为30 dB的高斯白噪声，如图2所示。

图2 原始波形Fig.2 Original waveform

1）最优采样频率的选取

根据本文3.2节所提出的方法，先以较高的采样频率10000 Hz采集数据80 ms得到800个数据点，再分别以每10、12、17、20、25个点进行各倍率的抽取得到采样频率分别为1000 Hz、833 Hz、588 Hz、500 Hz、400 Hz的数据，分别用这些数据形成方程组（12）（模型阶数均取为0.4倍的数据点数），再利用式（20）进行灵敏度计算，得出结果见表1。

表1 各采样频率所对应的灵敏度Tab.1 Sensitivities corresponding to each sampling frequency

由表1可知，采样频率在588 Hz时所对应的灵敏度最小，所以取此时的数据进行Prony运算。

2）Prony辨识结果

应用本文所提算法得到的Prony辨识结果及误差分析如表2所示（已按能量从大到小排序，仅列出11项中的前8项），原信号波形与辨识结果拟合出的信号波形的误差曲线见图3。

由此可知，本算法在信噪比为30 d B强噪声环境中各参数的辨识误差均很小，辨识结果与原信号十分接近。

表2 Prony算法辨识结果及误差分析Tab.2 Identification results of Prony algorithm and error analysis

3）真实频率成分的提取

根据本文第4节所提出的方法，当把各结果分量的能量从大到小排序，能量迅速减小时，可以认为后面的分量是虚假分量。

由图4可知前3个分量是真实的频率成分，后面的分量是由噪声引起的，与原信号的情况相符。

图3 原始波形与Prony算法拟合波形的误差曲线Fig.3 Error curve of the original waveform and the fitting wave of the Prony algorithm

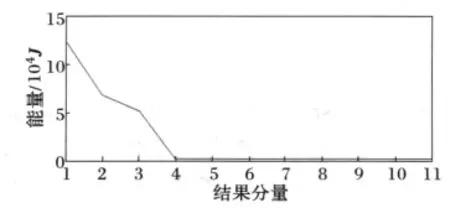
图4 Prony辨识结果各分量的能量大小变化Fig.4 Energy variation of the Prony identification result components

（4）与原始Prony算法的比较

用本文所提出的方法和原始方法分别对原信号（仍为30 dB的信噪比但噪声不同）独立运算100次，计算耗时（PC机主频2.66GHz，480M内存）比较结果如表3所示，辨识精度比较结果如表4所示。在原始方法的计算过程中，还出现了几次“矩阵奇异”的警告。由此可知，本文所提方法的计算耗时明显优于原始方法，在辨识精度和稳定性方面也比原始方法好。

表3 本文方法和原始方法的耗时比较结果Tab.3 Time－consuming comparison of the proposed and original method s

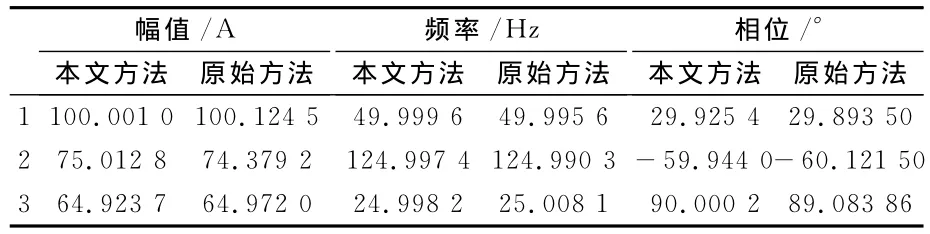
表4 本文方法和原始方法的辨识精度比较结果Tab.4 Identification accuracy comparison of the proposed and original method

6 结论

（1）本文提出的Prony算法改进方案应用于电力系统谐波的检测，无论是对工频整数次还是非整数次谐波，都能一次性地辨识出信号中各成分的幅值、频率、初相等参数，且具有较高的精度。

（2）本文提出了减少算法复杂度的方法，以及在线自适应采样频率选取方案、模型阶数和时间窗的选取原则，缩短了算法的计算耗时，提高了辨识精度。

（3）本文提出了真实频率成分的提取方法，解决了应用Prony算法进行谐波检测时较高模型阶数带来的虚假成分问题，进一步提高了Prony算法的可靠性。

［1］ 杨洪耕，惠锦，侯鹏（Yang Honggeng，Hui Jin，Hou Peng）.电力系统谐波和间谐波检测方法综述（Detection methods of harmonics and inter－harmonics in power system）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2010，22（2）：65－69.

［2］ 丁屹峰，程浩忠，吕干云，等（Ding Yifeng，Cheng Haozhong，LüGanyun，et al）.基于Prony算法的谐波和间谐波频谱估计（Spectrum estimation of harmonics and interharmonics based on Prony algorithm）［J］.电工技术学报（Transactions of China Electrotechnical Society），2005，20（10）：94－97.

［3］ 黄云江，谢维波（Huang Yunjiang，Xie Weibo）.基于迭代Prony算法的高精度谐波检测（Precise harmonic analysis based iterative Prony method）［J］.电气应用（Electrotechnical Application），2007，26（4）：97－100.

［4］ Costa F F，Cardoso A J M.Harmonic and interharmonic identification based on improved Prony＇s meth－od［C］∥32nd Annual Conference on IEEE Industrial Electronics，Paris，France：2006.

［5］ 束洪春.电力工程信号处理应用［M］.北京：科学出版社，2009.

［6］ Kamel N，Sankaran P，Venkatesh B.Fault－current predetermination using time－limited CT secondary side measurements by the covariance－Prony method［J］.IEE Proceedings：Generation，Transmission and Distribution，2004，151（6）：735－739.

［7］ 魏木生.广义最小二乘问题的理论和计算［M］.北京：科学出版社，2006.

［8］ 王治平，郑慧娆，张莉（Wang Zhiping，Zheng Huirao，Zhang Li）.Hankel矩阵类的一种快速分解算法（A fast decomposition algorithm of Hankel matrix class）［J］.数学杂志（Journal of Mathematics），1998，18（S1）：145－147.

［9］ Demeure Cedric J，Scharf Louis L.Fast least squares

solution of Vandermonde systems of equations［C］∥IEEE International Conference on Acoustics，Speech

and Signal Processing，Glasgow，Scotland：1989.［10］Lee Joon－Ho，Kim Hyo－Tae.Selecting sampling interval of transient response for the improved Prony method［J］.IEEE Trans on Antennas and Propagation，2003，51（1）：74－77.