李晓月，王 克，2

（1.东北师范大学数学与统计学院，吉林长春 130024；2.哈尔滨工业大学（威海）数学系，山东威海 264209）

无闭轨Lienard系统拓扑分类中结构α3β4和α3β6的实现

李晓月1，王 克1，2

（1.东北师范大学数学与统计学院，吉林长春 130024；2.哈尔滨工业大学（威海）数学系，山东威海 264209）

在对无闭轨Lienard系统完整拓扑分类72种的基础上，证明了其中与结构A＋B＋C＋D＋0相对应的16种拓扑结构，即结构α3β4－1，…，α3β4－4以及结构α3β6－1，…，α3β6－12都是可以实现的，并给出每一种拓扑结构具有实现性的充分条件.

Lienard系统；闭轨；拓扑分类；Gauss球面；Filippov变换

0 引言

众所周知，Lienard系统

其中f，ɡ：R→R连续，且xɡ（x）＞0，x≠0.它是一类经典的二阶微分系统，在医学、物理、机械、通讯等许多实践领域中都有着广泛的应用［1－2］，可以用来描述心脏的跳动，电路的循环，传送带的振荡器的作业以及通讯设备的工作状况等.它包含许多具有实际应用背景的具体方程为特例，譬如：van der Pol方程［3］

其中μ是正常数.以及在考虑无线电通信技术问题时［4－5］遇到的方程

其中L，r，C是正常数，分别代表感应系数、电阻和电容，x是电流强度.

由于在实践研究中的重要性，因而对方程（1）或它的等价平面系统

对于Lienard系统各种定性性质的研究，例如稳定性、解的有界性、振动性、极限环的问题以及其他定性性质的研究，已经有一批学者做了许多很好的工作.关于特定类型的微分系统的拓扑分类问题无疑是基本的理论问题，其解决将使人们对该类微分系统的认识进一步的深化，对各种性质的研究工作具有很大的推动作用，对应用技术的研发提供一个统一的理论平台.

文献［6－9］曾研究结构稳定的没有极限环的二次系统的拓扑分类问题，文献［10］研究了在系统轨道具有镜像对称性条件保证下，Lienard系统相平面轨线的拓扑分类问题.这些工作虽然都已经取得很大进展，但至今，问题仍未彻底解决.由此可以看出拓扑分类问题一般是难度较大且非常繁杂的.

Lienard系统是一种基本的微分系统.但对无条件限制的Lienard系统的拓扑分类问题，目前系统的研究工作还很少.一个主要原因是Lienard系统一般来说并不是多项式系统.因此使用研究二次系统拓扑分类的方法来研究Lienard系统是很困难的.文献［11－14］采用了不同于文献［6－9］的方法研究了无闭轨Lienard系统的拓扑分类问题，得到了完整的结果，证明了无闭轨Lienard系统共有72种可能的拓扑结构.

对于无闭轨Lienard系统进行拓扑分类是重要的，但是对于拓扑分类的可行性和实现性的证明更加重要，因为只有这样，才更能说明该种分类的合理性和意义.以往很少有文献在对Lienard系统进行拓扑分类的基础上，考虑其实现性的问题.在此方面文献［10］做了一些很好的工作.但所考虑的Lienard系统都是有条件限制的，因此对于Lienard系统的分类并不是彻底的，可能存在的拓扑结构要少很多，实现性的证明也要简单一些.

为此，我们在文献［11－14］对无闭轨Lienard系统进行完整拓扑分类的基础上，证明了72种可能存在的拓扑结构的每一种都是有可能实现的，即举出满足一定条件的Lienard方程的例子来说明其具有72种可能存在的拓扑结构的一种.本文证明了其中的16种拓扑结构都是可以实现的，并给出每一种拓扑结构具体实现的充分条件.

在本文中，考虑了比方程（1）稍广泛的平面系统方程（5）是无闭轨的.令

采用和文献［11］相同的记号，把系统（5）的轨线分为以下5类：

定理1无闭轨Lienard系统（5）的轨线可以分为9类：第一类用A＋0表示，包括所有其轨线属于A∪O的无闭轨Lienard系统；第二类用B＋0表示，包拓所有其轨线属于B∪O的无闭轨Lienard系统；第三类用A＋C＋0表示，包括所有其轨线属于A∪C∪O的无闭轨Lienard系统.类似的，其余6类分别是：B＋C＋0，A＋D＋0，B＋D＋0，A＋C＋D＋0，B＋C＋D＋0，以及A＋B＋C＋D＋0.它们的定义完全可以类似上面写出，此处从略.为方便起见，把原点O（0，0）记为点0.

定理2在Gauss球面上，0点有3种可能性：（α1）没有椭圆扇形；（α2）有一个有界椭圆扇形；（α3）有一个无界椭圆扇形.

定理3在Gauss球面上，奇点∞有如下6种可能性：（β1）没有椭圆扇形；（β2）只有一个有界椭圆扇形（不连接0与∞）；（β3）只有两个有界椭圆扇形，此外无其他D类轨线；（β4）只有一个无界椭圆扇形；（β5）有两个有界椭圆扇形，且存在D类轨线，它与∞点构成的奇闭轨所围成的闭区域包含这两个椭圆扇形在内；（β6）只有一个有界椭圆扇形和一个无界椭圆扇形.

定理4若α3，β4成立，则系统（5）有4种可能的拓扑结构：α3β4－1，α3β4－2，α3β4－3和α3β4－1.

定理5若α3β6成立，则系统（5）有12种可能的拓扑结构：α3β6－1，α3β6－2，…，α3β6－12.

本文的主要安排如下：首先证明了4种拓扑结构α3β4－1，…，α3β4－4是可以实现的，并给出每一种拓扑结构具体实现的充分条件；接着证明了拓扑结构α3β6－1，…，α3β6－12都是可以实现的，并给出每一种拓扑结构具体实现的充分条件.

其中F，ɡ：R→R连续，且F（0）＝0，xɡ（x）＞0，x≠0，且总假设系统（5）的轨线满足唯一性.本文总假设

Filioppov变换的方法［15］在Lienard系统的研究工作中有广泛的应用.我们在今后也要大量应用这个方法，首先对Lienard系统（5）作Filippov变换，则

1 4种α3β4结构的实现

1.1 α3β4－1，…，α3β4－4的实现

首先在右半平面考虑Lienard系统

易见（8）式的奇点0是一个退化结点.容易证明对Y＋上的任意点A，γ＋（A）必与F＋相交于点B，然后进入奇点0.令点A沿Y＋向上方趋于无穷，则B点将沿直线y＝2x向右上方趋于无穷.作直线x＝1，设直线x＝1与直线y＝2x相交于点C.则当y A足够大时，将有y B＞y C.这时γ＋（B）将与直线x＝1相交于点D.当点A沿Y＋向上运动时，D点将沿直线x＝1向下运动，但始终保持在点（1，0）的上方.故当A沿Y＋向上方趋于无穷时，D点必有极限点D＊，且y D＊≥0.容易证明y D＊＞0.

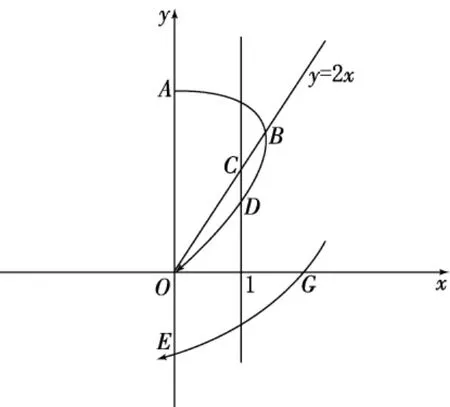
图1 方程（8）的局部轨线结构

在Y－上任取一点E，则γ－（E）必与直线x＝1相交于G.令E点沿Y－向上趋于点0，则G点沿直线x＝1向上运动，并趋于点G＊.显然应有y G＊≤y D＊.见图1.下面我们要证明y G＊＝y D＊，即G＊＝D＊.

容易求出（8）式的通解为

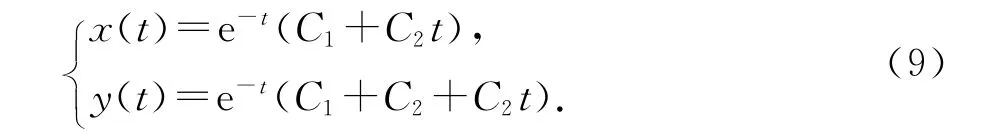
其中C1，C2为任意常数.在直线y＝2x上取点B（a，2a），a＞0，则容易求得过点B的（8）式的轨线γ（B）的方程为

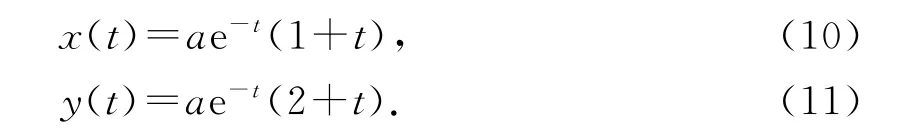
由（11）式减（10）式得

由（11）式比（10）式得

因为a＞0，由（13）式易见y D＞1.故y D＊≥1.若y D＊＞1，则在（13）式的两端令a→＋∞，也就是令B点沿直线y＝2x向右上方趋于无穷.此时D→D＊，故（13）式的左端y D→y D＊.因为a→＋∞时，

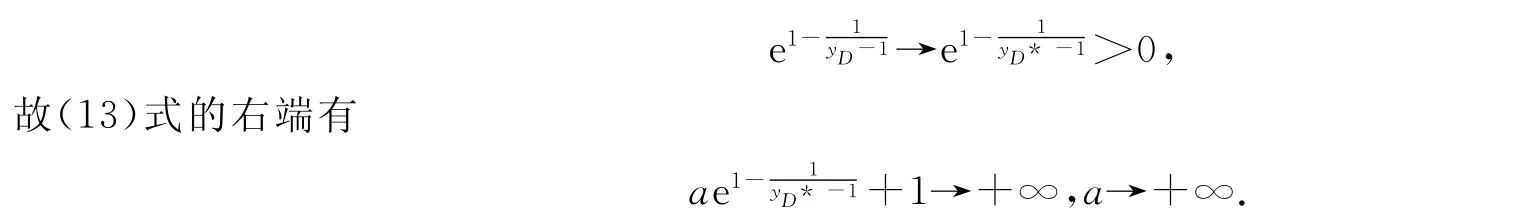
由此y D＊＝1，矛盾.即D＊的坐标为（1，1）.

取点e（0，b）∈Y－，b＜0.则由（9）式求得过点E的（8）式的轨线γ（E）的方程为

类似上面的证明，由（14），（15）式消去t得到

用类似上面的分析得到如下的结论：在直线y＝－2x上任取一点H，则γ＋（H）必与Y＋相交于点I，而γ－（H）将进入奇点0.若x H＜－1，则γ－（H）必与直线x＝－1相交于点J.当点H沿直线y＝－2x向左上方趋于无穷时，I点将沿Y＋向上方趋于无穷.而J点将向下趋于一点J＊，且y J＊＝1.在Y－上任取一点E，则γ＋（E）将与直线x＝－1相交于点K，当点E沿Y－向上趋于点0时，K点将向上趋于点J＊.

现在考虑平面Lienard系统

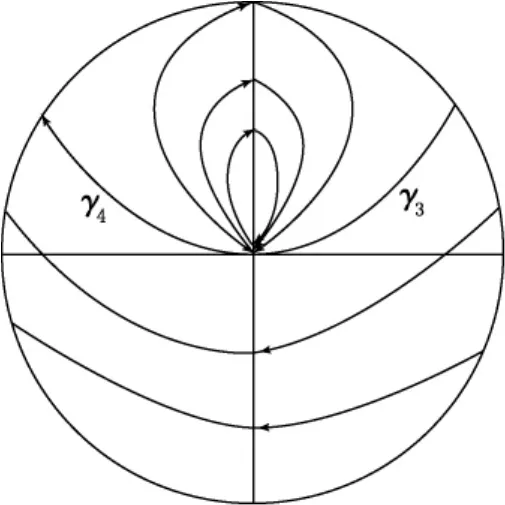
图2 方程（19）的轨线结构

综合上面对系统（8）和系统（18）的讨论.我们断言在Gauss球面上，系统（19）的奇点0具有一个无界的椭圆扇形，∞点具有一个无界的椭圆扇形.而γ（D＊）∈A和γ（J＊）∈B为这两个椭圆扇形的分界线.0点和∞点没有抛物扇形.因而系统（19）具有结构α3β4－1.见图2，为了方便起见，今后我们仍用通常的方式，把系统的全局结构画在一个圆内，但要注意把整个圆周看成一个点，即∞点.

现在令

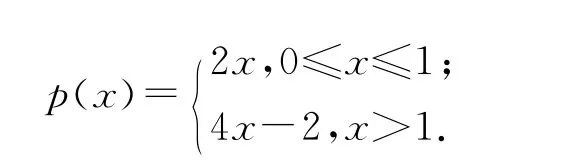
我们在右半平面考虑方程

在折线y＝p（x）上取点A1，x A1＞1.设过点A1的系统（8）和系统（20）的轨线分别为γ（8）（A1）和γ（20）（A1）.显然当x＞1时有p（x）＞2x；而当0≤x≤1时，p（x）＝2x.

γ（＋20）（A1）必与直线x＝1相交于点L.令点A1沿折线y＝p（x）向右方运动，则点L将沿直线x＝1向下运动，由比较定理易知，γ＋（8）（A1）位于γ＋（20）（A1）的右下方.由此推得y L≥y D＊.因而若A1点沿折线y＝p（x）向右方趋于无穷时，L点将沿直线x＝1向下趋于某一点L＊，且y L＊≥y D＊.

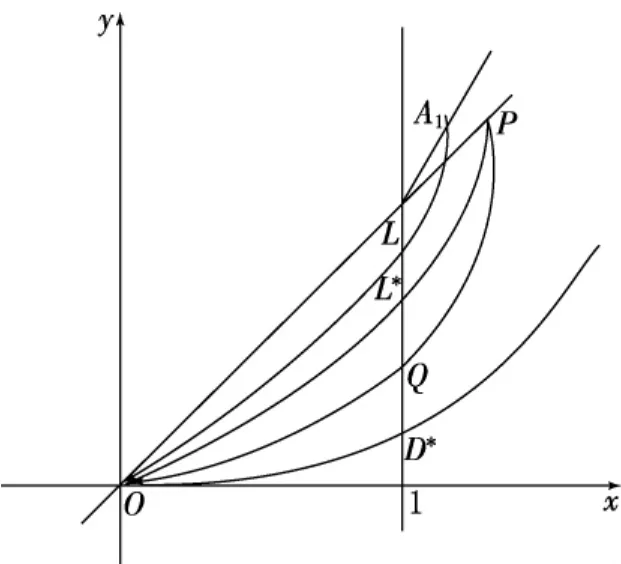
图3 方程（20）的局部轨线结构

由上面的讨论易知Lienard系统

具有结构α3β4－2.见图4.

图4 方程（21）的轨线结构

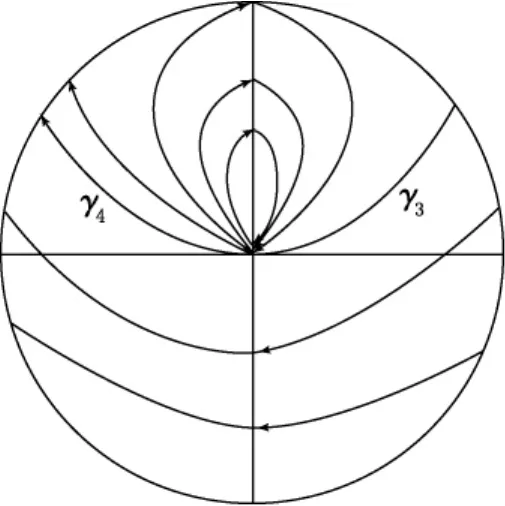
图5 方程（22）的轨线结构

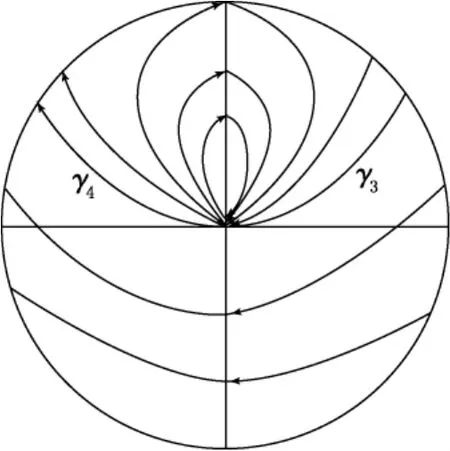
图6 方程（23）的轨线结构

具有结构α3β4－4.见图6.于是我们已证明了如下定理：

定理6拓扑结构α3β4－1，α3β4－2，α3β4－3和α3β4－4都是能够实现的.

1.2 一般性定理

定理7设G（±∞）＝＋∞.

注意函数P（u）与前面定义的函数p（x）在性质上的相似之处，在左半平面，系统（5）仍与系统（18）等价.完全类似于前面对系统（20）的讨论，我们可以对系统（28）施以同样的论证.可以证明，系统（28）的奇点0在右半平面有一个由A类轨线构成的抛物扇形.于是系统（5）的奇点0在右半平面也有一个由A类轨线构成的抛物扇形.亦即系统（5）也具有结构α3β4－2.

和2°的证明类似，3°和4°的证明也完全类似于对系统（22）的证明，以及对系统（23）的讨论.为简捷起见，此处从略.

2 12种α3β6结构的实现

2.1 α3β6－1，α3β6－7，α3β6－11的实现

设F1（z），z＞0，连续.F1（0）＝0，且满足：

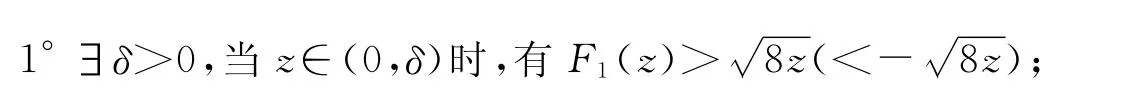
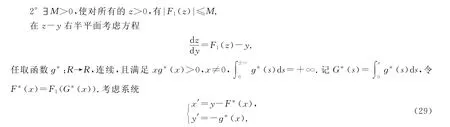
引理1系统（29）具有一个有界的椭圆扇形，椭圆扇形的外面被闭轨所充满.

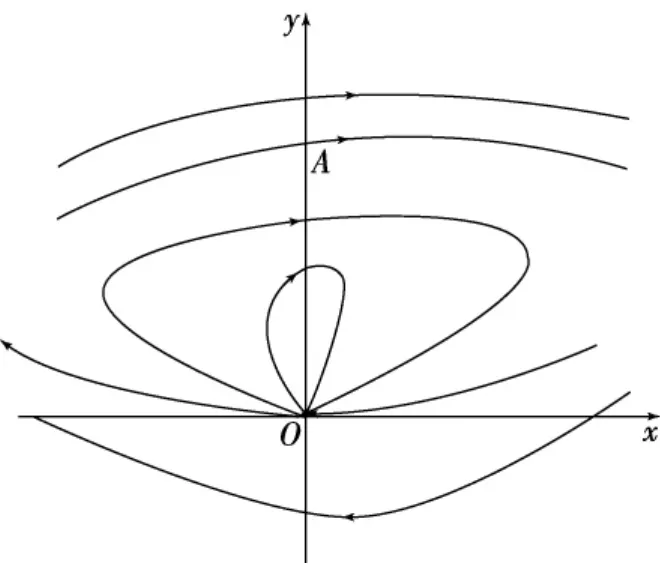
图7 方程（30）的局部轨线结构

证明对系统（29）实行Filippov变换，则系统（29）在右、左二半平面都与方程（6）等价.由条件1°知系统（29）的0点存在一个椭圆扇形.由条件2°知此椭圆扇形是有界的，且系统（29）无D类轨线.因为系统（29）在右、左二半平面都与方程（6）等价，由向量场的对称性易证椭圆扇形以外的系统（29）的轨线都是闭轨.

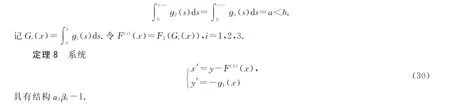
证明对系统（30）实行Filippov变换，则系统（30）在右、左二半平面都与方程（6）等价，其中z∈（0，b）.参考系统（29）的性质，容易证明如下结论：

（1）对Y＋上的点P，y P∈（0，y A），系统（30）的过点P的轨线γ（30）（P）∈C.0点的椭圆扇形的边界轨线向左右无限延伸.故系统（30）的0点有一个无界的椭圆扇形.

（2）对Y＋上的点P，y P≥y A，γ（30）（P）∈D.故∞点有一个有界的椭圆扇形.

（3）对任意点P∈Y－，γ（30）（P）∈D.故∞点还有一个无界的椭圆扇形.

（4）系统（30）只有一条A类轨线和一条B类轨线.它们在Filippov变换下，都对应于方程（6）的过点B的积分曲线在曲线y＝F1（z）下方的一段曲线.见图7.因而系统（30）具有结构α3β6－1.

定理9系统

具有结构α3β6－11.

证明对系统（31）实行Filippov变换，则系统（31）在右、左二半平面都与方程（6）（z∈（0，a））以及方程（7）（z∈（0，b））等价.

在z－y右半平面内的曲线y＝F1（z）上取点C（a，F1（a））.设方程（6）的过点C的积分曲线与Y＋相交于点D.因为a＜b，故点D在点A的下方.定义

设方程（6）的过点A的积分曲线与直线相交于点E和G，且y＜y.记点H为过点D的积分曲

GE线与直线的位于曲线y＝F（z）之下的交点.回到x－y右半平面.设点G和点H的对应点分别

1为G′和H′，γ（H′）∈A.它们都在直线x＝x H′上.而C点在对应点为y＝F（z）上的横坐标为∞的点.容易证明如下结论：

图8 方程（31）的局部轨线结构

（1）对任意的P∈Y＋，y P∈（0，y D），γ（31）（P）∈C，0点的椭圆扇形的边界轨线向右方无限延伸，故系统（31）的0点有一个有界的椭圆扇形；

（2）对任意的P∈Y＋，y P∈［y D，y A），γ（31）（P）∈B，0点有一个B类抛物扇形；

（3）对任意的P∈Y＋，y P≥y A，γ（31）（P）∈D，系统（31）的∞点有一个有界的椭圆扇形；

（4）对任意的P∈Y－，γ（31）（P）∈D，∞点有一个无界的椭圆扇形；

（6）系统（31）只有一条B类轨线向左趋于无穷，见图8.

因而系统（31）具有结构α3β6－11.

定理10系统

具有结构α3β6－7.

证明与定理9的证明类似.故从略.

2.2 α3β6－4，α3β6－12，α3β6－8的实现

设系统（5）满足G（±∞）＝＋∞，且对系统（5）实行Filippov变换后有z，z＞0.由定理7知系统（5）具有结构α3β6－1.即系统（5）的0点具有一个无界的椭圆扇形，位于上半平面；∞点具有一个无界的椭圆扇形；且系统（5）具有一条A类轨线和一条B类轨线，分别位于第一和第二象限.

取点A1∈Y＋.设方程（6）的过点A1的积分曲线与曲线y＝F1（z）相交于点B1.记z B1＝b1.取定a1∈（0，b1）.取ɡ1：R→R连续，满足xɡi（x）＞0，x≠0，i＝4，5，6.并且

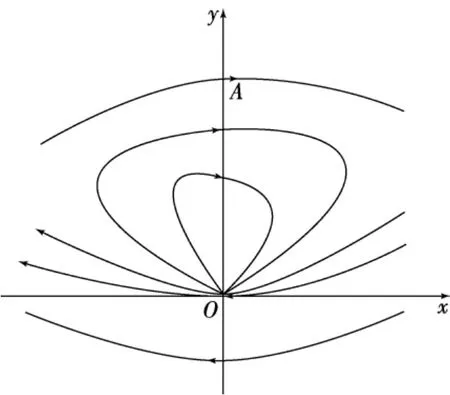
图9 方程（34）的局部轨线结构

（1）对任意的P∈Y＋，y P∈（0，y A1），γ（34）（P）∈C，0点的椭圆扇形的边界轨线向左右无限延伸，故系统（34）的0点存在一个无界的椭圆扇形；

（2）对任意的P∈Y＋，y P≥y A，γ（34）（P）∈D，∞点存在一个有界的椭圆扇形；

（3）对任意的P∈Y－，γ（34）（P）∈D，∞点存在一个无界的椭圆扇形；B类抛物扇形，见图9.

故定理11成立.

定理12系统

具有结构α3β6－12.

证明对系统（35）实行Filippov变换，则系统（35）在右、左二半平面分别与方程（6）（z∈（0，a1））以及方程（7）（z∈（0，b1））等价.

图10 方程（35）的局部轨线结构

（1）对任意的P∈Y＋，y P∈（0，y D1），γ（35）（P）∈C，0点的椭圆扇形的边界轨线向右方无限延伸，故系统（35）的0点有一个无界的椭圆扇形；

（2）对任意的P∈Y＋，y P∈［y D1，y A1），γ（35）（P）∈B，0点有一个B类抛物扇形；

（3）对任意的P∈Y＋，y P≥y A1，γ（35）（P）∈D，∞点有一个有界的椭圆扇形；

（4）对任意的P∈Y－，γ（35）（P）∈D，∞点还有一个无界的椭圆扇形；

故系统（35）具有结构α3β6－12.

具有结构α3β6－8.

证明与定理12的证明类似.故从略.

对以上的6种α3β6型结构，即α3β6－1，α3β6－4，α3β6－7，α3β6－8，α3β6－11和α3β6－12的实现问题，我们是采用把已知的结构向左右两边无限“拉开”的办法来获得所需要的结构.对其余6种α3β6型结构的实现问题，我们将采用“拼接”技巧来解决.

2.3 α3β6－5，α3β6－9，α3β6－6，α3β6－10，α3β6－2，α3β6－3的实现

引理2若（x（t），y（t）），t∈R，是系统（5）的轨线，则对任意k≠0，（kx（t），ky（t）），t∈R是系统

证明由ɡ7和F（7）的构造知，系统（38）的左半平面的相图等同于系统（30）在左半平面的相图，而系统（38）的右半平面的相图则是下面的系统（39）在右半平面的相图.由定理8知系统（30）具有结构α3β6－1.考虑系统

由引理2知系统（39）的相图是把系统（33）的相图以原点为中心扩大k1倍而得到的.由k1的定义知，k1D＝A.设k1A＝Q.于是由系统（33）的性质知：

证明系统（40）在右半平面的相图与系统（30）在右半平面的相图一样，而系统（40）的左半平面的相图则是由系统（31）在左半平面的相图以原点为中心扩大k1倍而得到的.其余证明类似定理14，此处从略.

系统（41）的相图是由系统（30）的右半相图与系统（34）的左半相图拼成的，而系统（42）的相图则是由系统（30）的左半相图与系统（34）的右半相图拼成的.详情从略.

［1］CESARI L.Asymptotic behavior and stability problems in ordinary differential equations［M］.Berlin：Springer－Verlag，1963：1－70.

［2］SANSONE G，CONTI R.Equazioni differenziali non lineari［M］.Roma：Cremonese，1956：20－100.

［3］VAN DER POL B.Sur les oscillations de relaxation［J］.The Philos Magazine，1926，7：978－992.

［4］CARTAN H，CARTAN E.Note sur la génération des oscillations entretenues［J］.Ann P T T，1925，14：1196－1207.

［5］CONTI R，SANSONE G.Non－linear differential equations［M］.New York：Pergamon，1964：35－81.

［6］SANTOS G T.Lecture notes in math［M］.Berlin：Springer，1977，597：605－640.

［7］蔡燧林.“关于一类二次系统的极限环存在的估计”一文的注记［J］.浙江大学学报：自然科学版，1979（4）：105－113.

［8］朱德明.结构稳定的无环二次系统的拓扑分类［J］.南京大学学报：自然科学版，1986，22（2）：263－273.

［9］史松龄.无环二次系统的拓扑分类［J］.中国科学院研究生院学报，1986（1）：1－120.

［10］SUGLE J，HARA T.Classification of global phase portraits of a system of lienard type［J］.J Math Anal Appl，1995，193：264－281.

［11］王克.无闭轨Lienard系统的拓扑分类（Ⅰ）：九种粗结构［J］.东北师大学报：自然科学版，1998，31（4）：1－6.

［12］王克.无闭轨Lienard系统的拓扑分类（Ⅱ1）：64种可能性［J］.东北师大学报：自然科学版，1999，32（2）：1－5.

［13］王克.无闭轨Lienard系统的拓扑分类（Ⅱ2）：64种可能性［J］.东北师大学报：自然科学版，1999，32（4）：14－18.

［14］王克，李晓月，李文学.无闭轨Lienard系统的8种新轨线结构［J］.东北师大学报：自然科学版，2010，42（3）：1－6.

［15］张芷芬，丁同仁，黄文灶，等.微分方程定性理论［M］.北京：科学出版社，1985：203－240.

Realization of the structuresα3β4andα3β6 based on the topological classification of lienard systems without closed orbit

LI Xiao－yue1，WANG Ke1，2

（1.School of Mathematics and Statistics，Northeast Normal University，Changchun 130024，China；2.Department of Mathematics，Harbin Institute of Technology（Weihai），Weihai 264209，China）

Lienard systems without closed orbit were given a complete classification with 72 kinds of possible topological structures.Based on the results，this paper prove that the 16 kinds of possible topological structures：α3β4－1，…，α3β4－4，α3β6－1，…，α3β6－12，can be realized and give the sufficient realization conditions.

Lienard systems；closed orbit；topological classification；Gauss sphere；Filippov transformation

O 175.12

110·44

A

1000－1832（2011）04－0001－12

2010－10－15

国家自然科学基金资助项目（10701020；11171056）；吉林省科技发展计划项目（20101593）；中国博士后科学基金资助项目

（20070420949）.

李晓月（1975—），女，博士，副教授，主要从事动力系统及应用微分方程理论研究；王克（1947—），男，博士，教授，博士研究生导师，主要从事微分方程理论及应用研究.

陶 理）