付文羽

（宁波工程学院 理学院，浙江 宁波 315211）

三维各向同性谐振子在两不同坐标下的解及其联系

付文羽

（宁波工程学院 理学院，浙江 宁波 315211）

根据量子理论及薛定谔方程，从三维各向同性谐振子的本征值与本征函数出发，详细研究了三维各向同性谐振子在直角坐标系和球面坐标系下的本征函数、本征值之间的对应关系。理论分析表明，直角坐标系两不同坐标系下的本征函数之间通过一个幺正变换联系起来，能级简并度与幺正变换矩阵阶数相同。

量子力学；三维各向同性谐振子；不同坐标系；本征函数

自然界中广泛碰到简谐运动，任何体系在平衡位置附近的小振动，例如分子的振动，晶格的振动，原子核表面振动以及辐射场的振动等，都可以按简谐振动进行处理。对于三维各向同性谐振子，常见的求解方法是将其在直角坐标系下分离变量，将三维薛定谔方程化为三个一维微分方程进行处理［1］。由于一维谐振子在直角坐标系下的本征函数及本征值早已被人们所熟知，所以通过这种方法很容易解出三维各向同性谐振子的本征值和本征函数。三维各向同性谐振子另一种解法就是在球面坐标系下，运用薛定谔方程的直接求解得出的本征函数。

上述两种解法均在文献［1，2］中进行了详细讨论。由于选择了不同的守恒量完全集，加之问题的复杂性，在直角坐标系下求得的本征函数为三个厄尔米特函数的乘积，而在直角坐标系下求得的本征函数为球谐函数与合流超几何函数的乘积。那么，一个有意思的问题是在这两个不同坐标系下解出的三维各向同性谐振子的本征值、本征函数之间有什么联系？本文通过两种坐标系下解的讨论，找出其本征值、本征函数之间对应关系，为不同的守恒量完全集下同一问题的讨论提供一个教学例证，同时，也促使学生加深对诸如厄尔米特函数、球谐函数与合流超几何函数等特殊函数性质的理解。

1 三维各向同性谐振子在两不同坐标系下解的简述

1.1 三维各向同性谐振子在直角坐标系下的解

三维各向同性谐振子在直角坐标系下的定态薛定谔方程为

令 Φ（x，y，z）＝Φ（x）Φ（y）Φ（z）分离变量得方程

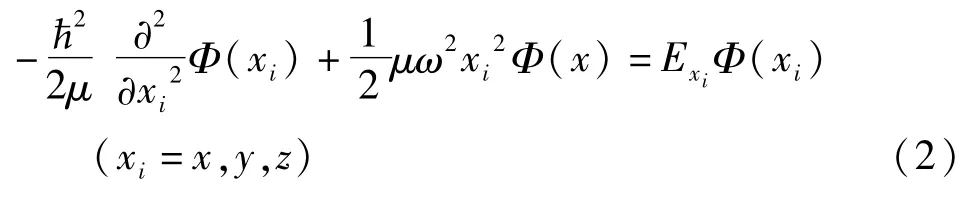
其 解［1］，因 此 方 程

（1）的本征函数为

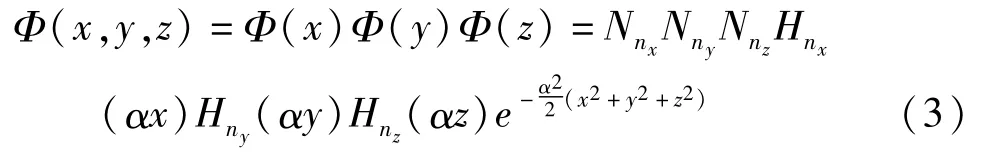
方程（2）的本征值为

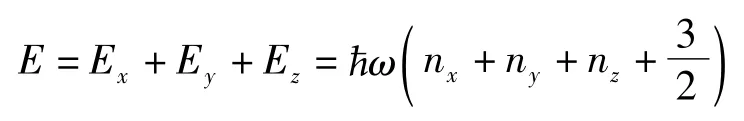
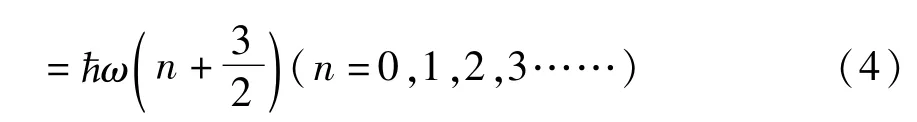
对于一组给定（nx，ny，nz）值，三维各向同性谐振子能级的简并度为其中 Ex＋Ey＋Ez＝E，f＝1＋2

1.2 三维各向同性谐振子在球坐标下的解

三维各向同性谐振子在球坐标下的定态薛定谔方程

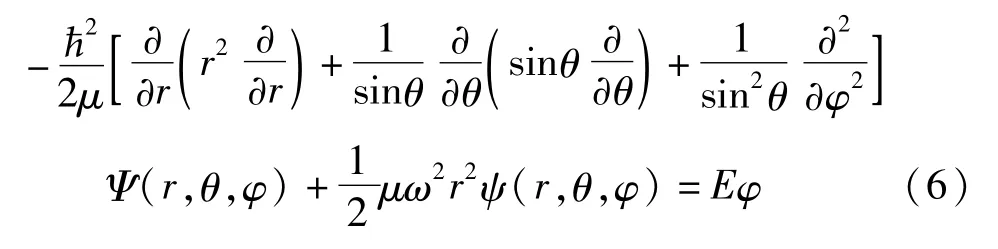
球坐标下三维各向同性谐振子的本征函数为Ψ（r，θ，φ）＝Rnrl（r）Yl，m（θ，φ）

其中，

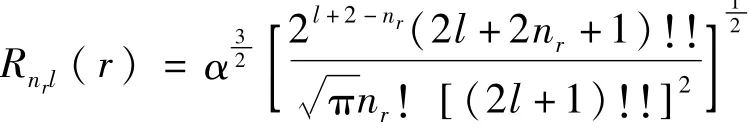
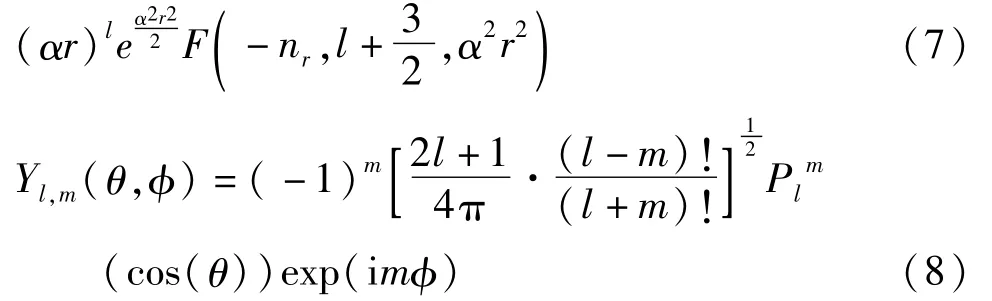
本征值为

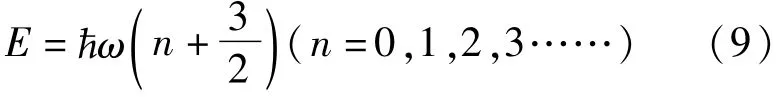
2 两种不同坐标下本征函数之间联系

由上述求解过程可知，两种求法的过程不尽相同，本征值的表达形式却完全相同，而且在直角坐标系下求解三维各向同性谐振子比较容易，表达形式也较简明，相比较而言，在求坐标下求解，过程较繁且结果也较繁。由于选择了不同的守恒量完全集，在球坐标系中求解得出的本征函数Ψnrlm（r，θ，φ）是守恒量完全集的共同本征态，而在直角坐标系中求解得出的本征函数 Φ（x，y，z）则是守恒量完全集的共同本征态，根据态和力学量的表象变换理论，我们假设这两个本征函数由一个幺正变换联系起来。

下面对上述假设进行验证。

（1）对于n＝0，由于能级不简并，可以看出这

两个本征函数是相同的，即

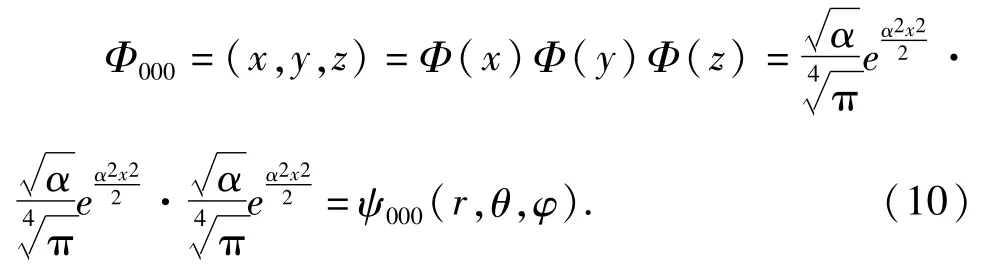
（2）对于 n＝1，能级简并度为 3，波函数 ψnrlm（r，θ，φ）三个态分别为

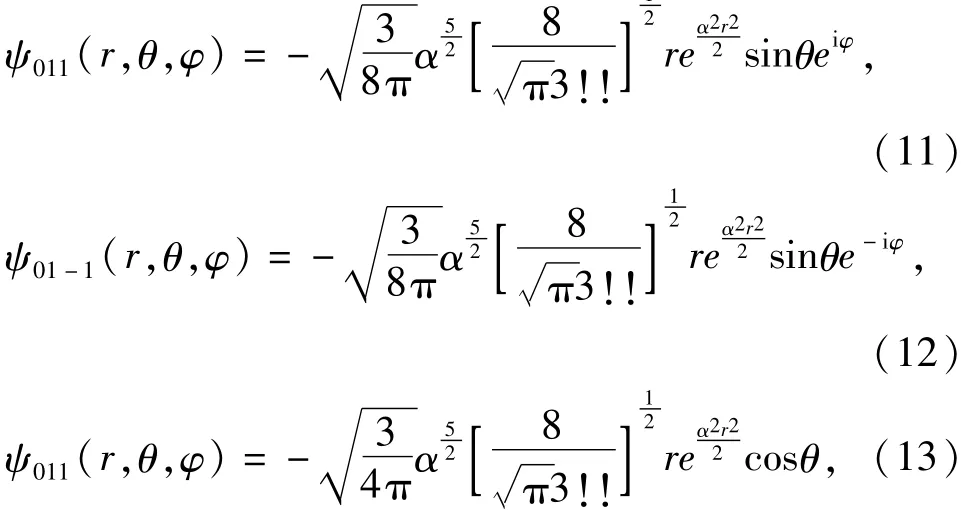
1

波函数 Φnxnynz（x，y，z）三个态分别为

代入（11）、（12）、（13）式得

式（17）（18）（19）式与（14）（15）（16）式对比可知所以归一化的幺正变换为（3）对于n＝2，能级简并度为 6，ψnrlm（r，θ，φ）有 6个态为

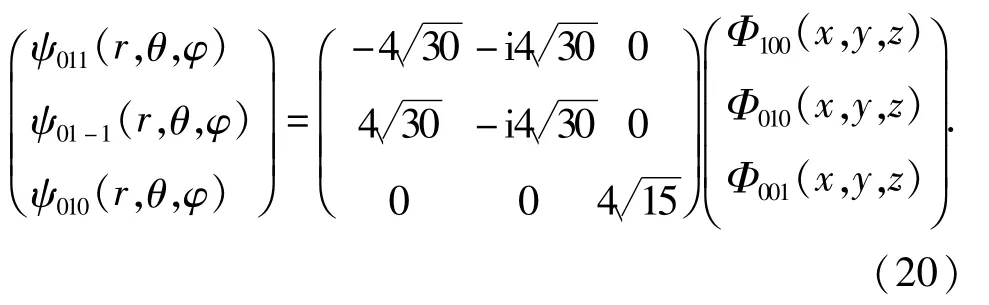
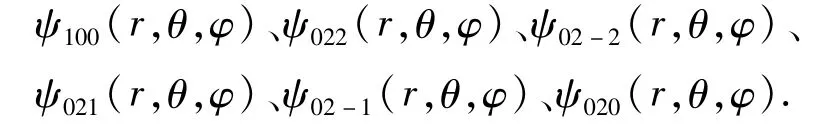
Φ（x，y，z）也有6个态分别为

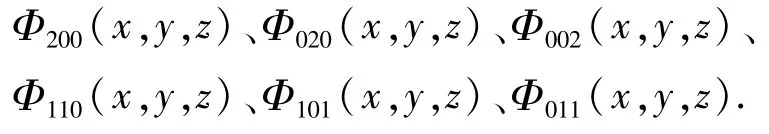
由于

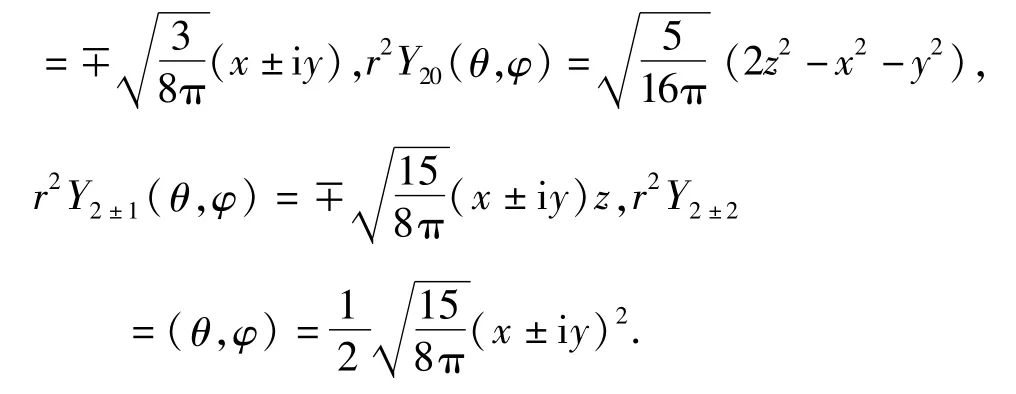
所以我们可以将 ψn，lm（r，θ，φ）表示为 Φ（x，y，z）的函数得

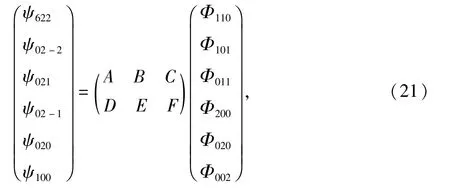
其中其中分块矩阵

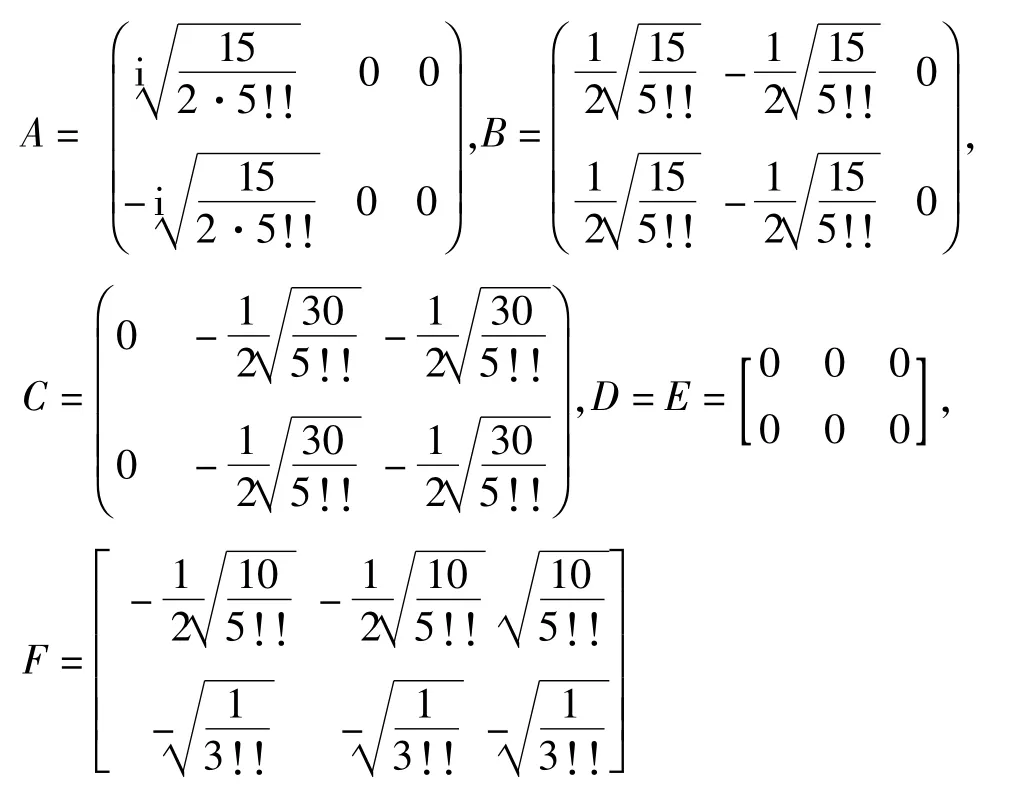
由此可得 n＝2时的幺正变换为

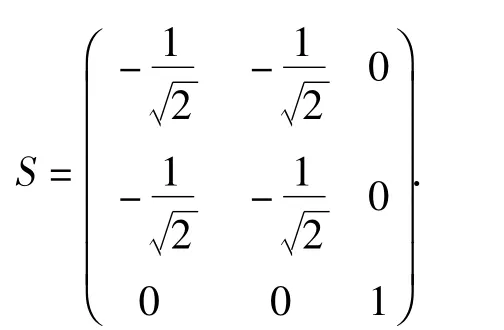
（4）对于 n＝3，能级简并度为10，用同样方法分析可得n＝3的情况下：ψn，lm（r，θ，φ）＝SΦ（x，y，z）波函数ψn，lm（r，θ，φ）与Φ（x，y，z）之间的幺正变换为一个10阶矩阵

其中分块矩阵

3 结论

由以上分析计可知，三维各向同性谐振子在直角坐标系下和在球面坐标系下的本征函数之间通过一个幺正变换联系起来，即三维厄尔米特函数与球谐函数和合流超几何函数之间通过一个幺正变换相互联系起来，这就印证了量子力学中两不同守恒量完全集之间的变换是一个幺正变换的结论。同时，也给出了厄尔米特函数、球谐函数和合流超几何函数之间的关系。这对于理解这几类特殊函数的性质和量子力学教学具有参考价值。

根据以上计算，我们得出，在n＝1时，三维各向同性谐振子的能级简并度为3，求出的幺正变换是3阶矩阵。在n＝2时，三维各向同性谐振子的能级简并度为6，求出的幺正变换是6阶矩阵，在n＝3时，能级的简并度为10，求出的幺正变换是 10阶矩阵，依次类推，我们可以断定，在 n＝N时，由于能级的简并度为（N＋1）（N＋2），所以得出的幺正变换应为（N＋1）（N＋2）阶矩阵。

［1］曾谨言.量子力学教程［M］.北京：科学出版社，2003.

［2］周世勋.量子力学［M］.北京：高等教育出版社，1979.

［责任编辑 贺小林］

Results and Relationship of Three－Dimensional Isotropic Harmonic Oscillator in the Two Different Coordinate System s

FUWen－yu
（Faculty of Science，Ning bo University of Technology，Ning bo 315211，China）

Based on the theory of quantum and schrodinger function，it discussed particularly the corresponding relationship of eigenfunctions and eigenvalue for three-dimensional isotropic harmonic oscillator in cartesian coordinate and in spherical coordinate respectively.The theoretical results show that the eigenfunctions in cartesian coordinate and in spherical coordinate are associated by unitary transformation，and the degeneracy of energy level is same with the order of unitary transformation.

quantum mechanics；three－dimensional isotropic harmonic oscillator；different coordinate systems；eigenfunction.

G642.41

A

1004-602X（2011）01-0019-04

2010 -12 -27

甘肃省高校研究生导师科研项目计划（0810－1）；宁波工程学院科研启动项目

付文羽（1963—），男，甘肃宁县人，教授，硕士。