(徐州师范大学 数学科学学院,江苏 徐州 221116)

0 引言

随机偏微分方程是偏微分方程或Banach空间中常微分方程的随机扰动,对其可积性与解的研究越来越受到众多数学家和物理学家的重视,而随机波方程是随机偏微分方程的一个重要研究课题.带随机扰动的可积系统的研究始于1983年,M.Wadati利用反散射方法构造非线性随机KdV方程的精确解[1].XIE[2,3]首先在Wick型随机波方程这一领域开展工作,并取得了大量研究成果.本文在此基础上利用白噪声分析理论,截断展开方法[4]研究了(2+1)维Wick型随机ANNV孤子系统:

(1)

其中⦿是Kondratiev分布空间(S)-1上的Wick型积,A(t),B(t),Γ(t)和D(t)均为(S)-1值白噪声泛函,且A(t)⦿D(t)≠0,B(t)≠-Γ(t).

式(1)的变系数ANNV孤子系统为:

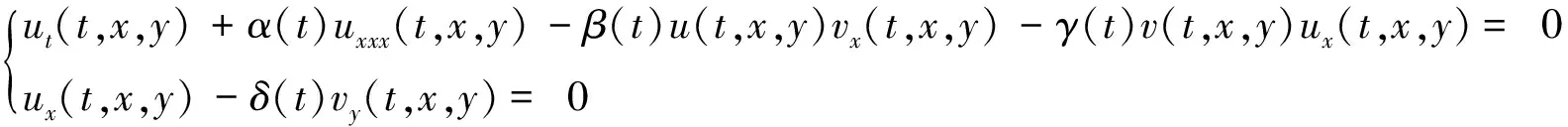
(2)

其中α(t),β(t),γ(t),δ(t)为t的函数,且α(t)δ(t)≠0,β(t)≠-γ(t).

式(2)源于(2+1)维非对称Nizhnik-Novikov-Veselov(ANNV)孤子系统:

(3)

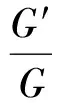
1 (2+1)维Wick型随机ANNV系统的解

为了得到随机孤子系统的解,由文献[2]中定理2.1,当d=2时,对(1)进行Hermite变换,得到下面:

(4)

这里z=(z1,z2,…)∈CN是向量参数.简记

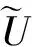
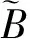
则(4)表示为:

(5)

其中α(t,z),β(t,z),γ(t,z),δ(t,z)是关于t,z的函数.令

u(t,x,y,z)=u(ξ),v(t,x,y,z)=v(ξ)

(6)

其中ξ=k(t,z)x+l(t,z)y+s(t,z)+c0,在这里k(t,z),l(t,z),s(t,z)是关于t,z的待定函数,且k(t,z)l(t,z)≠0,c0是任意常数.

将(6)式代入(5)有

k(t,z)u′(ξ)-δ(t,z)l(t,z)v′(ξ)=0,

对其积分一次并令积分常数为零得

从而有常微分方程

(xkt(t,z)+ylt(t,z)+st(t,z))δ(t,z)l(t,z)u′(ξ)+

α(t,z)δ(t,z)l(t,z)k3(t,z)u‴(ξ)-k2(t,z)(β(t,z)+γ(t,z))u(ξ)u′(ξ)=0

(7)

2(xkt(t,z)+ylt(t,z)+st(t,z))δ(t,z)l(t,z)u(ξ)+2α(t,z)δ(t,z)l(t,z)k3(t,z)·

u″(ξ)-k2(t,z)(β(t,z)+γ(t,z))u2(ξ)=0

(8)

设(8)有如下形式的解

(9)

其中ai(t,z)(i=0,1,…,n)是关于t,z的待定函数,F(ξ)满足:

(10)

利用齐次平衡法平衡(8)中最高阶偏导项与非线性项得n=2,于是(9)式可写成:

u(ξ)=a0(t,z)+a1(t,z)F(ξ)+a2(t,z)F2(ξ)

(11)

注意到

u′(ξ)=a1(t,z)F′(ξ)+2a2(t,z)F(ξ)F′(ξ)

(12)

u″(ξ)=a1(t,z)F″(ξ)+2a2(t,z)F′2(ξ)+2a2(t,z)F(ξ)F″(ξ)

(13)

将(10)～(13)式代入方程(8),由于含有F(ξ)的各次项线性无关,从而可得:

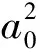
F(ξ):a1(t,z)k3(t,z)α(t,z)l(t,z)δ(t,z)-a0(t,z)a1(t,z)k2(t,z)(β(t,z)+γ(t,z))+

a1(t,z)l(t,z)δ(t,z)st(t,z)=0,

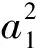
2a0(t,z)a2(t,z))(β(t,z)+γ(t,z))-2a2(t,z)l(t,z)δ(t,z)st(t,z)=0,

F3(ξ):(2a1(t,z)-10a2(t,z))k(t,z)α(t,z)l(t,z)δ(t,z)-a1(t,z)a2(t,z)(β(t,z)+

γ(t,z))=0,

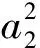
xF2(ξ):a2(t,z)kt(t,z)=0,yF2(ξ):a2(t,z)lt(t,z)=0.

从上述可以发现kt(t,z)=lt(t,z)=0,从而记k(z)=k(t,z),l(z)=l(t,z),通过Mathematic软件,再利用(11)式得:

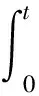
此情形(5)的截断展开解为:

(14)

其中

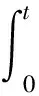
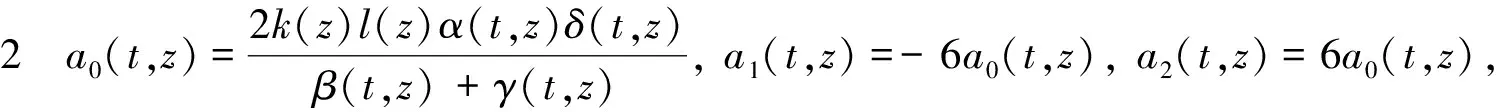
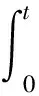
此时(5)的截断展开解为:

(15)

其中

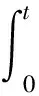
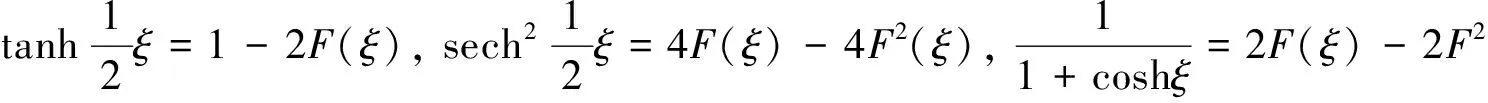
(16)

其中

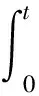
(17)

由(5)的解,存在有界开集G⊂R+×R2及q>0,r>0,u(t,x,y,z),ut(t,x,y,z),ux(t,x,y,z),v(t,x,y,z),vx(t,x,y,z),vy(t,x,y,z)及uxxx(t,x,y,z)对(t,x,y,z)∈G×Kq(r)一致有界,对(t,x,y)∈G连续,其中z∈Kq(r).由文献[2]定理2.1知,存在U(t,x,y),V(t,x,y)∈(S)-1,使得u(t,x,y,z)=HU(t,x,y)(z),v(t,x,y,z)=HV(t,x,y)(z),且U(t,x,y),V(t,x,y)是(1)在空间(S)-1上的强解.

因此可得(1)的白噪声泛函解,即有如下结果.

定理1 设U(t,x,y),V(t,x,y)分别是u(t,x,y,z),v(t,x,y,z)的Hermite逆变换,且满足随机偏微分(1),令N(t)=kA(t)⦿(B(t)+Γ(t))⦿(-1),则有U(t,x,y),V(t,x,y)白噪声泛函的具体表示:

注: 如果在没有随机干扰的环境下将所有的Wick积变成普通积,那么可以得到(2+1)维变系数ANNV系统(2)的显式精确解.

2 小结

1)Wick-型泛函一般很难计算,然而可以给出一些非Wick-型的白噪声泛函作为随机偏微分方程的特殊解,如文献[8]中的例子.Wiener白噪声空间与Possion白噪声空间之间存在一个酉映射,通过这个单一映射可以由Gaussian SPDEs的解得到Possion SPDEs的解[9],从而可以给出(1)的Possion白噪声泛函解.

2)求解随机偏微分方程是一件较困难的事情,而截断展开方法是一种非常简便有效的工具,可以用来求得一大类Wick-型随机可积系统的白噪声泛函解,本文中得到了(2+1)维随机非对称Nizhnik-Novikov-Veselov孤子系统的解,对于更高维的情形也可以做类似讨论,这里不再论述.

[1]Wadati M.Stochastic Korteweg-de Vries equation[J].J Phys Soc Jpn,1983,52: 2642-2648.

[2]Xie Y C.Exact solutions for stochastic KdV equations [J].Phys Lett A,2003,310(2):161-167.

[3]Xie Y C.Exact solutions for stochastic mKdV equations[J].Chaos Solitons &Fractals,2004,20(2):337-342.

[4]张解放,陈跃芳.截断展开方法和广义变系数KdV方程新的精确类孤子解[J].物理学报,2001,50(9):1648-1650.

[5]Boiti M,Leon J P,Manna M,et al.On the spectral transform of a KdV equation in two spatial dimensions[J].Inver Prob,1986(2):271-279.

[6]李帮庆,马玉兰.(G′/G)展开法和(2+1)维非对称Nizhnik-Novikov-Veselov系统的新精确解[J].物理学报,2009,58(7):4373-4378.

[7]周振春,马松华,方建平,等.(2+1)维孤子系统的多孤子解和分形结构[J].物理学报,2010,59(11):7540-7545.

[8]Chen B.White noise functional solutions of Wick-type stochastic NLS equations[J].Mathematica Applicata,2010,23(2): 292-298.

[9]Benth F E,Gjerde J.A remark on the equivalence between Possion and Gaussian stochastic partial differential equations[J].Potential Analysis,1998,8(2):179-193.