赵学智，叶邦彦

(华南理工大学机械与汽车工程学院 广州 510640)

近年来奇异值分解(singular value decomposition,SVD)在图像处理、系统辨识、控制理论、信号处理、故障检测与诊断等很多领域得到了广泛的应用。将SVD应用于工程实际所需解决的关键是实现其数值计算(一般用QR算法实现)。本文首先系统地总结了一般矩阵数值计算文献中所介绍的QR算法的特点，给出了一个该算法在处理由某些小幅度信号构造的大矩阵的奇异值分解时不收敛的具体实例，进而研究了产生该不收敛现象的本质原因。通过对QR迭代过程中Givens矩阵变化特点的理论分析，对算法的收敛特性进行了深入的解剖，指出该算法在处理大型矩阵的SVD时不收敛的根本原因在于首行对角带元素的衰减，并进一步得到了一个关于首行元素的衰减对QR算法收敛速度影响的重要结论，利用实例数据进行证实，为多次分割、双向收缩QR算法的提出奠定了基础。

1 奇异值分解的数值计算问题

SVD的数值计算并不容易，在一些文献中，矩阵A的奇异值分解是通过计算AAT和ATA的特征值和特征向量实现的[2-5]。由于该二类矩阵是对称阵，利用Jacobi方法[2-3]可计算出其特征值和特征向量。但是，该方法有两个缺点：

(1) 计算AAT或ATA的运算量较大；

(2) 在计算AAT或ATA时，由于存在舍入误差，会导致信息损失，有时甚至会导致计算所得到的奇异值面目全非。

文献[1]提出了一种直接计算SVD的方法，首先利用Householder变换将A化为上双对角线矩阵，再利用带隐式位移的QR算法将上双对角线阵化为对角线阵，可分别得到U、S、V。文献[6-8]针对一些特殊的矩阵如正定Toeplitz矩阵、Hessenberg矩阵等，对该算法提出了一些相应的改进措施。文献[9-10]提供了基于文献[1]提出的QR算法实现SVD的数值计算程序。但是由于该算法本身的原因，这些程序都对其中的QR迭代总次数做出了限制，因而其可处理的矩阵阶数绝不可能很大。

2 单向收缩QR算法

该上双对角化过程比较简单，值得研究的是在完成了上双对角化过程后，再对矩阵B执行QR迭代以最终实现对角化时，当矩阵阶数很大，在QR迭代时如果不注意收缩方向的选择、矩阵的分割、非零元素的不同方向驱逐等因素，则QR算法就有可能出现不收敛的情况。

QR迭代是通过一系列Givens平面旋转矩阵实现的，Givens平面旋转矩阵是一个正交矩阵：

式中c=cosθ；s=sinθ；除了已标示出的矩阵元素外，其余位置的元素全部为零。

设阶数为d的上双对角方阵B的通用形式为：

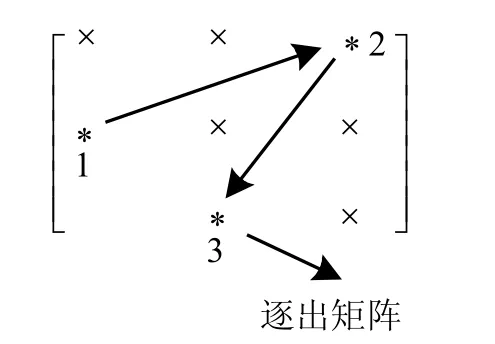
图1 非零元素的驱逐过程

式中 0为零矩阵；bd,d为分离出来的一个奇异值。此时矩阵可以向上收缩一行，得到矩阵B1，虽然其仍然是一个上双对角阵，但是其阶数已降为d−1。继续对B1执行同样的QR迭代运算，矩阵将持续向上收缩，其阶数不断降低，新的奇异值不断地被分离出来，最终可以实现整个矩阵的对角化。

从步骤4可见，执行QR迭代时，矩阵按照从下到上的方向收缩，故可称此QR迭代为单向收缩QR算法。处理阶数不大的矩阵时，该算法可实现较快的SVD计算。但在基于SVD方法的信号处理中，经常要利用信号构造一个大阶数的矩阵，其行列数一般可达成千上万[13]。在实践中发现，如果信号的幅值较小，而构造的矩阵阶数又很大，则按照上述算法对这些大矩阵进行SVD运算，有时会出现不收敛的情况。例如，该算法在处理某些小幅度信号所构造的大型矩阵时，在矩阵向上收缩了一定的行数之后，设此时的上双对角阵为Bi，再对Bi进行QR迭代时，不管QR迭代过程被执行多少次，Bi最右下角的次对角元却始终会停顿在某一个数值，再也无法下降，不能满足式(5)的收敛准则，矩阵无法收缩下去，这就是以上QR算法在实际应用时可能出现的问题。实际上，文献[9-10]在其提供的计算SVD的QR算法程序中，也已经认识到该算法在处理某些大矩阵时可能会出现不收敛的情况，但是该文献未能解释出现该问题的原因，也未提出解决措施，仅仅在程序中设计了迭代一定次数后不收敛就强行终止程序的指令。按照最乐观的估计，即使一次QR迭代完成后能平均实现两行的向上收缩，算法程序所能处理的矩阵阶数最多为QR迭代总次数的两倍，实际处理时远远不可能达到这一目标，因此它们都难以用于计算大型矩阵的奇异值分解。根据奇异值理论，对于任何矩阵，不管其阶数有多大、行数与列数孰大孰小，其奇异值分解总是存在且总是可以实现其数值计算的，算法出现不收敛的情况只能说明算法存在问题，有待改进。

3 单向收缩QR算法的不收敛实例

本文通过一个具体实例证明该QR算法在处理由某些实际信号所构造的大型矩阵时会出现不收敛的情况。

图2所示为一个长度为1 024点的铣削力信号，以该信号构造一个行数512、列数513的Hankel矩阵。通过Householder变换将其化为上双对角阵后，利用QR算法对其进行对角化。开始时矩阵向上收缩的速度很快，一般只需执行一次QR迭代(最多只执行3次)，矩阵就可向上收缩一行。当向上收缩了113行即收缩到第399行时，QR迭代总共被执行了168次后，此后再也无法满足收缩条件。执行到第174次QR迭代后，上双对角阵Bi最右下角的次对角元b398,399的值停顿在2.019 732×10−5，再也无法下降，算法陷入无限循环。

图2 一个铣削力信号

图3所示为前200次QR迭代时，矩阵末行向上收缩的变化情况。图中清晰地反映了刚开始时矩阵末行快速向上收缩以及之后收缩终止的过程。

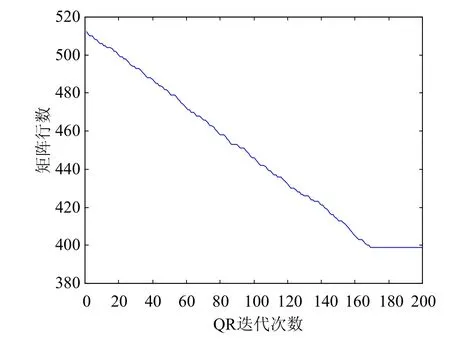
图3 QR迭代时矩阵末行的收缩过程

4 单向收缩QR算法的收敛特性分析

本文通过对QR迭代过程中Givens矩阵变化特点的研究和分析，发现引起上述问题的根源在于第一个Givens右矩阵。设矩阵向上收缩了一定行数之后的上双对角阵为Bi，在对其进行QR变换时，根据式(2)可得QR变换中的第一个Givens右矩阵中c和s的值分别为：

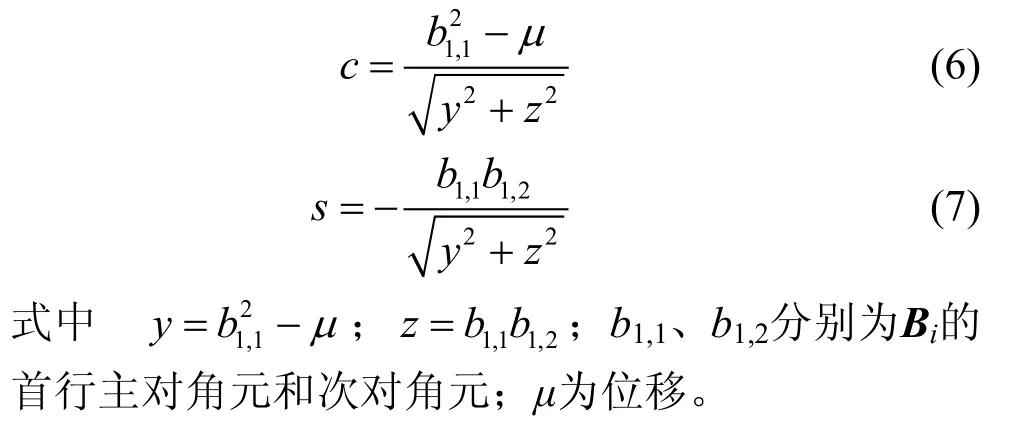
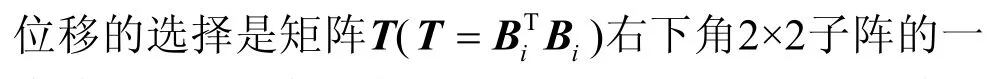
从表1可见，s第6个值的数量级是10−10，非常接近零，表明第6次QR迭代开始时G1(1,2,)θ已接近为单位阵。但是，从图4可以看出，此时上双对角阵Bi的末行却依然能以很快的速度向上收缩。可是根据前面的分析，当第一个Givens右矩阵G1为单位阵时，后续的其他一系列左、右Givens变换矩阵肯定是单位阵，此时式(4)的QR变换将失去意义，Bi再也不可能向上收缩了。

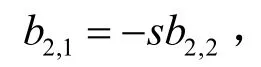
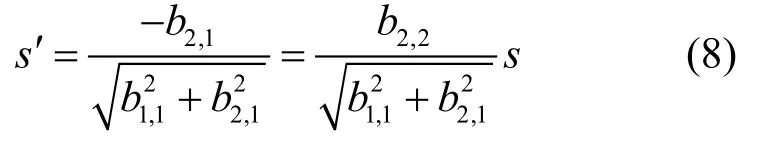
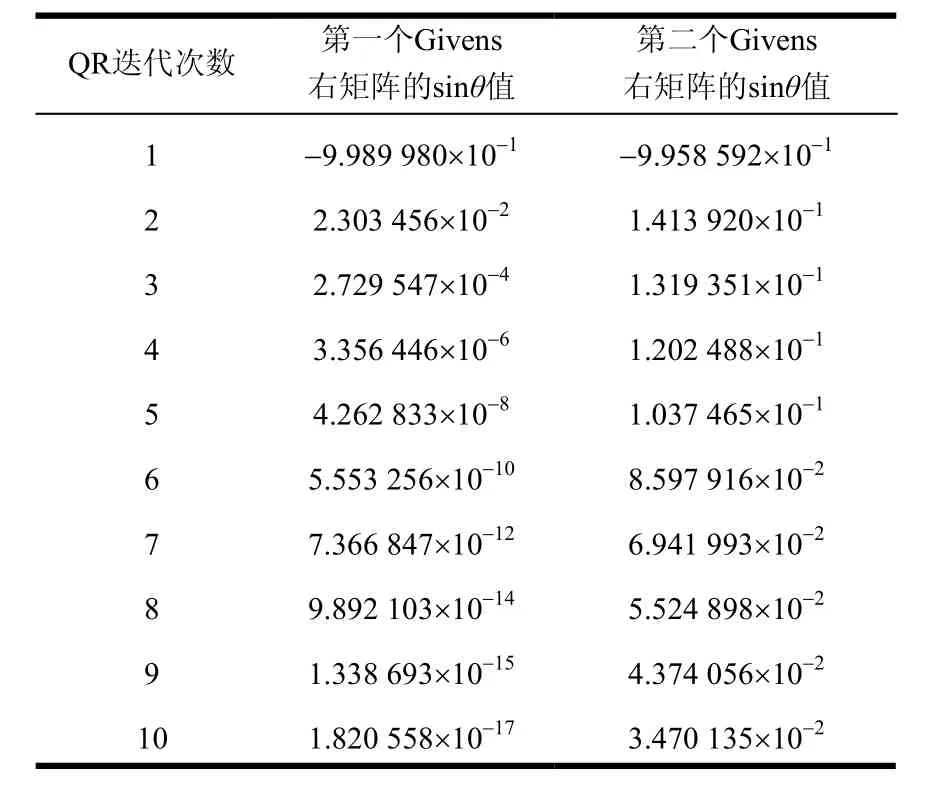
表1 前10次QR迭代时前两个Givens右矩阵的sinθ值

由图2可见，构造矩阵的铣削力信号中所有数据的数量级都是一样的，也即矩阵A中所有元素的数量级都相同，而经过Householder变换后所得的上双对角阵B的两个对角带元素的数量级仍然与矩阵A是一致的，则由式(8)易见，s′和s的数量级是相同的。因此，当第一个Givens右矩阵接近单位阵时，第一个Givens左矩阵也将接近单位阵，其变换的结果是在位置(1,3)处产生新元素：

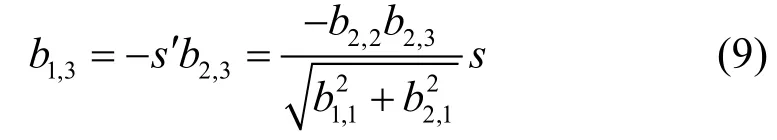
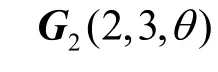
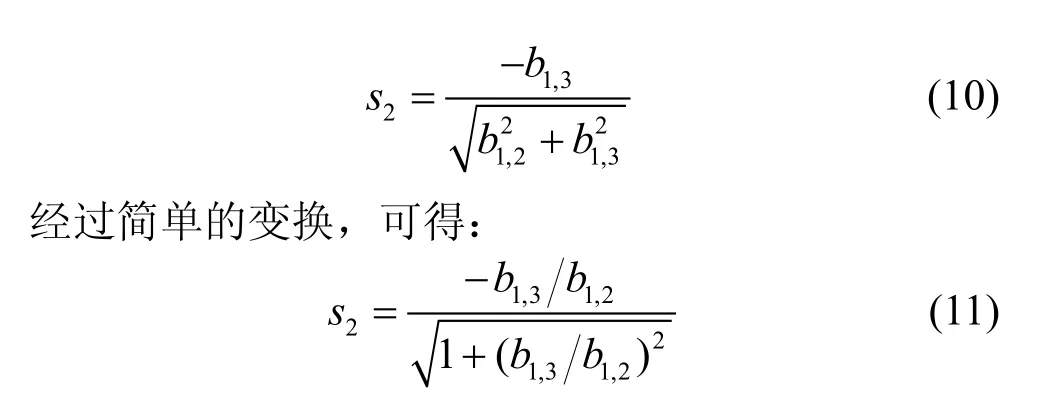
从式(7)可知，第一个Givens右矩阵的s的数量级是由b1,1和b1,2的乘积决定的，当s较小时，表明b1,1或者b1,2的数量级也较小。由于b1,1是主对角带元素，为未来的奇异值，其衰减的可能性比b1,2小很多，因此更可能是b1,2的数量级与s接近，则式(11)中的比值b1,3/b1,2的数量级反而会增大。例如假设s的数量级为10−11，由于构造矩阵的信号数据的数量级为10−1，可以认为此时b1,1的数量级亦为10−1，则由式(7)可得此时b1,2的数量级为10−10；而由前述可知，b1,3的数量级将最多比s的数量级小10−1，因此可以认为b1,3的数量级为10−12，此时b1,3和b1,2都很接近于零；然而b1,3/b1,2的数量级却为10−2，则由式(11)可知第二个Givens右矩阵已经不是单位阵。

本文给出该例中第二个Givens右矩阵的前10个sinθ值，将它们列在表1中第3列。可见第10次QR迭代开始时，第一个Givens右矩阵的sinθ的数量级已下降为10−17，但第二个Givens右矩阵中sinθ的数量级却还只为10−2，证明以上的分析是正确的。这种结果将直接导致从第二个Givens右矩阵开始的后续一系列左、右Givens变换矩阵都不会是单位阵，从而使得以后的QR变换可正常进行，因此矩阵仍可快速向上收缩。

但是当矩阵阶数大到一定程度时，如果原始矩阵中数据的数量级较小，有时在还没有完成整个矩阵的对角化的情况下，随着QR迭代次数的增加，第一个Givens右矩阵的sinθ有可能会完全下降为零，这会视原始矩阵数据的数量级而定。当该数量级较大时很难出现这种情况。但是一旦出现这种情况后，所有的左、右Givens变换矩阵都会变为单位阵，上双对角阵Bi最右下角的次对角元就会停顿在某一个数值，再也不能下降，算法陷入无限循环。表2给出了该例中QR迭代到第165～第174次期间，第一、二个Givens右矩阵中的sinθ值的变化过程。由表可见，在用8个字节表示一个实数的double数据类型编程的情况下，s的数量级可下降为10−323，而此时第二个Givens右矩阵的sinθ值的数量级却仅为10−5。迭代到第174次时，s终于完全降为零，第二个Givens右矩阵的sinθ值也随即变为零。此后所有的左、右Givens变换矩阵都变为单位阵，QR算法失效。

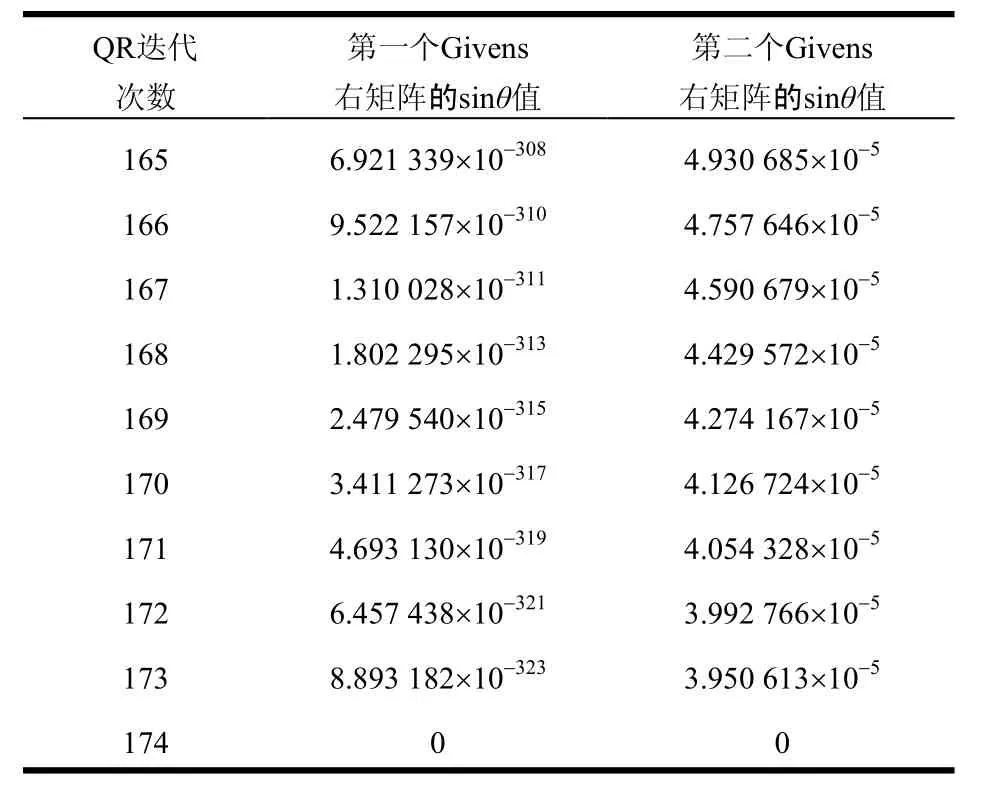
表2 第165～第174次QR迭代时前两个Givens右矩阵的sinθ值

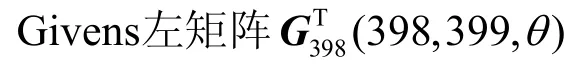
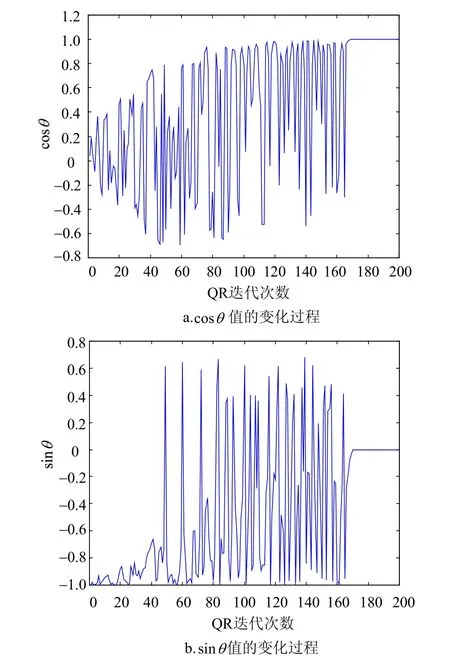
图4 中的cosθ和sinθ值的变化过程

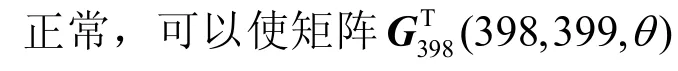
总结上述分析，可以得到关于QR算法的收敛特性的论断：在对双对角阵执行QR迭代时，除非第一个Givens右矩阵中的s完全为零，否则即使该s的数量级很小。但是，从第二个Givens右矩阵开始，后续的一系列左、右Givens变换矩阵却都不会相应地接近单位阵，从而可以使后面的QR迭代能正常进行。这就是在第一个Givens右矩阵中s的数量级相当小，即该矩阵非常接近单位阵的情况下，QR算法仍能实现矩阵快速向上收缩的原因。

5 结 论

(1) 在处理由某些小幅度信号构造的大型矩阵的奇异值分解时，单向收缩QR算法会出现不收敛的情况。

(2) 不收敛的本质原因在于矩阵首行对角带元素的衰减，当构造原始矩阵的信号数据的数量级较小时，这种衰减最终会使QR迭代中的第一个Givens右矩阵变为单位阵，从而导致后面的一系列Givens变换矩阵全部成为单位阵，使得QR算法失效。

(3) 当第一个Givens右矩阵十分接近单位阵时，从第二个Givens右矩阵开始，后续的一系列左、右变换矩阵却都不会相应地接近单位阵，使得QR算法仍然有很快的收敛速度。只有当第一个Givens右矩阵完全成为单位阵时，后续所有的Givens变换矩阵才会成为单位阵，QR算法才会完全失效。

上述工作为多次分割、双向收缩QR算法的提出指明了方向。该算法还涉及较多的与SVD收敛速度和精度相关的细节和技巧，其具体实现将另文进行探讨。

本文的研究工作得到广州市科技计划项目(2008J1-C101)的资助，在此表示感谢。

[1] GOLUB G H, VANLOAN C F. 矩阵计算[M]. 袁亚湘译.北京: 科学出版社, 2001.GOLUB G H, VANLOAN C F. Matrix computations[M].Translated by YUAN Ya-xiang. Beijing: Science Press,2001.

[2] DRMAC Z, VESELIC K. New fast and accurate Jacobi SVD algorithm(I)[J]. SIAM Journal on Matrix Analysis and Application, 2006, 29(4): 1322-1342.

[3] DRMAC Z, VESELIC K. New fast and accurate Jacobi SVD algorithm (II) [J]. SIAM Journal on Matrix Analysis and Application, 2006, 29(4): 1343-1362.

[4] NORDBERG T, GUSTAFSSON I. Using QR factorization and SVD to solve input estimation problems in structural dynamics[J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195(7): 5891-5908.

[5] VANLANDUIT S, CAUBERGHE B, GUILLAUME P.Reduction of large frequency response function data sets using robust singular value decomposition[J]. Computers and Structures, 2006, 84(12): 808-822.

[6] MASTRONARDI N, VANBAREL M, VANDEBRIL R. A fast algorithm for computing the smallest eigenvalue of a symmetric positive-definite Toeplitz matrix[J]. Numerical Linear Algebra with Applications, 2008, 15(4): 327-337.

[7] NIE Y Y, LI Z, HAN J D. Origin-shifted algorithm for matrix eigenvalues[J]. International Journal of Computer Mathematics, 2008, 85(9): 1397-1411.

[8] EIDELMAN Y, GOHBERG I, GEMIGNANIL L. On the fast reduction of a quasiseparable matrix to Hessenberg and tridiagonal forms[J]. Linear Algebra and Its Applications,2007, 420(1): 86-101.

[9] 徐士良. 数值方法与计算机实现[M]. 北京: 清华大学出版社, 2006.XU Shi-liang. Numerical methods and computer realization[M]. Beijing: Tsinghua University Press, 2006.

[10] 丁 军, 杨丽丽. 科学与工程数值算法(Java版)[M]. 北京: 清华大学出版社, 2003.DING Jun, YANG Li-li. Science and engineering numerical algorithms (Java Edition)[M]. Beijing: Tsinghua University Press, 2003.

[11] 奚梅成. 数值分析方法[M]. 合肥: 中国科学技术大学出版社, 2007.XI Mei-cheng. Numerical analysis methods[M]. Hefei:China Science and Technology University Press, 2007.

[12] 李庆扬, 王能超, 易大义. 数值分析[M]. 北京: 清华大学出版社, 2001.LI Qing-yang, WANG Neng-chao, YI Da-yi. Numerical analysis[M]. Beijing: Tsinghua University Press, 2001.

[13] 赵学智, 叶邦彦. SVD和小波变换的信号处理效果相似性及其机理分析[J]. 电子学报，2008, 36(8): 1582-1589.ZHAO Xue-zhi, YE Bang-yan. The similarity of signal processing effect between SVD and wavelet transform and its mechanism analysis[J]. Acta Electronica Sinica, 2008,36(8): 1582-1589.