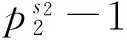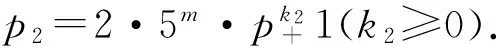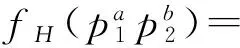具有循环4阶Sylow 2-子群的POS群
2010-01-19沈如林
沈如林
(湖北民族学院 数学系,湖北 恩施 445000)
1 介绍及引理
本文中的群G都表示有限群.如果x∈G,记o(x)是元x的阶, |X|表示集合X的阶,π(G)={p|p是|G|的素因子}.正如文献[1],G由元x∈G的阶子集(或,阶类)定义为集合OS(x)={y∈G|o(y)=o(x)}.显然,对于每个x∈G,OS(x)都是G的一些共轭类的分离并.群G叫做完全阶子集的群(简称G为POS-群),如果对于G的所有元x都有|OS(x)|是|G|的因子.在文献[1],Finch和Jones首先分类了交换的POS-群.之后继续研究了非交换的POS-群,并且给出了一些非可解的POS-群的例子[2,3].最近,Das给出了一些POS-群的性质,在文献[4]中分类了阶为2m的POS-群,其中(2,m)=1.本文继续文献[4]的研究,分类了Sylow 2-子群为循环的4阶群的POS-群.如果S是G的子集,记fS(m)为S中m阶元的个数.设U(n)是环Z/Zn的单位群,记ordn(q)为q在群U(n)中的阶.先给出一些引理.
引理1[3]如果G的每个元素的阶是一个素数幂且可解,则|π(G)|≤2.
一个2-Frobenius群G=ABC,这里A和AB是G的正规子群,AB和BC都是Frobenius群且分别以A,B为核,B,C为补.另外G称为一个Cpp-群,如果每个非平凡的p-元的中心化子都是一个人p-群.引理2归于Gruenberg和Kegel[6].
引理2 设G是一个可解的Cpp-群,则G是一个p-群,Frobenius群或2-Frobenius群.
引理3[7]设G是有限群,则阶能够被n整除的元的个数为0,或是与n互素的|G|的最大因子.
引理4[8]设G是一个非循环的且每个Sylow子群都循环的群,则:
G=
使得rn≡1(modm),|G|=mn且(n(r-1),m)=1.
引理5 设|G|=2npm且Sylow p-子群P在G中正规.如果G的Sylow子群循环且G没有2pm阶元,则G是Frobenius群.
证明根据引理4有:G=
r2n≡1(modpm)且(2n(r-1),pm)=1.
根据以上条件能够得到2n是r在U(pm)的阶.事实上,否则如果r的阶ordpm,(r)(∶=o(r))小于2n,则:
abo(r)=aro(r)=a1=a,
因此bo(r)}∈CG(P).一方面,因为CG(P)=1,bo(r)=1,与o(b)=2n矛盾.很容易看出阶ordpi(r)也是2n,这里1≤i≤n-1.因此每个非单位的p-元的中心化子为P,于是G是Frobenius群.
为了完成本文主要结果的证明,还需要素数的一些结果.称am-1的本原素因子rm(a),如果rm(a)|am-1,但是对于所有i 引理6 除了rm(a)=r6(2)或m=2且a=2k-1,本原因子一直存在. 引理7 设qn-1至少有一个本原素因子且n≥3,则: Φn(q)=(P(n),Φn(q))·Zn(q), 这里P(n)是n的最大素因子,Zn(q)是qn-1的包含所有n次本原因子的最大因子. 证明根据文献[10]及文献[11]有: Zn(q)|Φn(q)|Zn(q)·P(n),于是:Φn(q)=(P(n),Φn(q))·Zn(q). 引理8[12]设p是qk-1奇本原素因子,则p|Φf(q)当且仅当对于某个j≥0有:f=kpj. 另外还介绍一下p-进制数的概念.设Qp记作有理数的p-进制域,并设Zp为Qp的整数环,即p-进制整数的环.因此对于任意的正整数都能写成p的一个幂和的形式: 这里ai是{0,1,…,p-1}中的数.进一步对于给定整数m,系数ai在上面的那个m的p-进制分解唯一确定. 以下给出本文的主要结果. 定理1 设G是一个Sylow2-子群为4阶循环群的POS-群,则3是|G|的一个因子,或G是下列群之一: (a)4阶循环群; (b)Frobenius群Z5m∶4; (c)拟二面体群 证明设H是正规2-补.如果对于每个p∈π(H)有4不整除p-1,则因为π(H)的素数最小的一定是费马素数,有3∈π(H).以下假设π(H)有素数p使得4|p-1,则H是一个Cpp-群,因此根据引理2,H是Frobenius或2-Frobenius.注意π(H)中只有一个素数p满足以上的条件[6].以下分为两种情形: (1) 这里j,s,t≥0且1≤u≤2.以下要证明对于i=1,2有si=1. 因为i≤2,则l=1,矛盾.当t>0,则方程(1)变为: (2) (3) 如果k2>0,则方程(3)成为: 16·54k-1+8·53k+8·52k+4·5k+1=(2·5k1(2·5k+1)k2+1)t. (4) 认为以上的数为一个5-进制数.方程(4)的左边部分的第一和第二位为4·5k+1,且右边的为2t·5k1+1.明显,t<5.因此k=k1且t=2.进一步,方程(4)的左边的5-进制数为: 3·54k+54k-1+53k-1+3·53k+52k+1+3·52k+4·5k+1. 但是右边项的最高次数大于或等于2k(k2+1),则k2=1.很容易看出方程(4)的右边项是: 16·54k-1+8·53k+8·52k+4·5k+1, 矛盾. 如果k2=0,则方程(3)变为: 16·54k-1+8·53k+8·52k+4·5k+1=(2·54k-1)t (5) 根据上面的数的5-进制数的分解,可以看出k=k1.比较方程(5)两边的最高次数,有t≤4.很容易看出对于每个方程(5)中的那样的t方程都不成立. 如果s1=p1,则根据引理7和8,方程(1)变为: (6) (7) 不难看出方程(7)中左边的最大的次数大于右边的,矛盾.因此s1=1. (8) 如果K是p-群,则对于每个q∈π(L)有fH(q)整除4|L|.但是因为4不整除q-1且π(L)中最小的素数为费马素数,有3∈π(L). 情形ⅡH为2-Frobenius群.同样,假定H=ABC,这里A,B,C同上.明显,换位子群H′=AB.如果3不整除|H|,不难看出H满足一个4阶的固定点自由的自同构.则H′是幂零的[13],矛盾. 情形ⅢH为p-群.显然,p=5.根据文献[8]的命题8,Sylow5-子群,即H循环.设|H|=5m.另外G的Sylow2-子群是自中心化的,因此G不循环,则: G= 使得r4≡1(mod 5m)且(r-1,5m)=1.如果a的中心化子为,则根据引理5有G是Frobenius群.如果|CG(a)|=2·5m,则r2≡1(mod 5m).因为(r-1,5m),有r≡-1(mod 5m),因此: G= [1] Ashish Kumar Das.On Finite Groups Having Perfect Order Subsets[J].International Journal of Algebra,2009,13(3):629-637. [2] Gorenstein Daniel.Finite groups[M].NewYork:Chelsea Publishing Co.,1980. [3] Higman G.Finite groups in which every element has prime power order[J].Journal of the London Mathematical Society,1957,32(3):335-342. [4] Feit W.On large Zsigmondy primes[J].Proc Amer Math Soc,1988,102:29-36. [5] Finch C E,Jones L.A curious connection between Fermat numbers and finite groups[J].Amer Math Monthly,2002,109:517-524. [6] Finch C E,Jones L.Nonabelian groups with perfect order subsets[J].JP J Algebra Number Theory Appl,2003,3(1):13-26. [7] Finch C E,Jones L.Corrigendum to:“Nonabelian groups with perfect order subsets”[J].JP J Algebra Number Theory Appl,2004,4(2):413-416. [8] Malle G,Moreto A,Navarro G.Element orders and Sylow structure[J].Mathematis-che Zeitschrift,2006,252(1):223-230. [9] Ribenboin P.The book of prime number record[M].New York:Second Edition,Springer-Verlag,1989. [10] Shen R.A Note on Finite Groups Having Perfect Order Subsets[J].International Journal of Algebra,2010,13(4):643-646. [11] Williams J S.Prime Graph Components of Finite Groups[J].J Alg,1981,69:487-513. [12] Weisner L.On the number of elements of a group,which have a power in a given conjugate set[J].Bull Amer Math Soc,1925,31:492-496. [13] Zsigmondy K.Zur Theorie der Potenzreste[J].Monatsh Math und Phys,1892,3:265-284.2 主要结果