曹香莲,李 灿

(红河学院数学学院,云南蒙自 661100)

0 引 言

记,ex= (ex1,ex2,…,exn)T,AiT= (aijl)n×ki,bi=(bi1,bi2,…,biki)T,i=0,1,…,m,j=1,2,…,n, l=1,2,…,ki,则上述问题转化为,

乘子法是人们熟悉的一类约束非线性优化方法,其数值稳定好,计算过程简单,其中Fletcher提出的增广乘子法[1]最受重视.精确增广Lagrange函数方法[2-6]是把无约束问题定义在原问题变量与乘子变量的乘积空间.而几何规划是特殊的非线性规划,许多非线性优化的方法均可以应用到它中来.本文利用等式约束几何规划的精确增广Lagrange函数[7],结合收敛快、效率高的拟牛顿法[8],再利用几何规划的特点,给出了一类有效的求解等式约束优化问题的算法,并在适当条件下,证明了该算法的全局收敛性.

引理1 问题(GPE2)为一凸规划.

我们构造问题(GPE2)的精确增广Lagrange函数为,

1 几何规划问题

考虑等式约束下的广义几何规划的一般形式,

如果令xj=lntj,j=1,2,…,n,则(GPE)可转化为如下等价形式:

式中,λ=(λ1,λ2,…,λm)T是问题(GPE2)在最优解 x=x＊时的拉格朗日乘子的一个近似,C(x)= (C1(x),C2(x),…,Cm(x))T,σ＞0为罚因子.

由式(1)可得到,

由此可构造如下方程组,

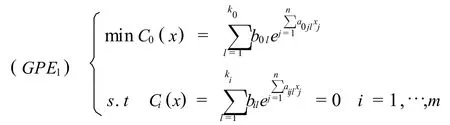
式中,Bk为Lagrange函数的二阶导数矩阵的某种近似,令,

显然,Bk与 ▽C(xk)Bk▽C(xk)T是非奇异的,则式

(2)的解为,

假设,▽C(k)=[▽C1(x),▽C2(x),…,▽Cm(x)],对一切 x∈Rn行满秩.

定理1 设x＊与λ＊满足x＊是问题(GPE2)的严格局部极小点的二阶充分条件,则存在σ＊＞0,使对所有的σ≥σ＊,x＊为L(x,λ＊,σ)的一个无约束极小点;反之,若有 Ci(x—)=0,1≤i≤m,并且x—是L(x,λ,σ)对于某个λ—的无约束极小点,则 x—为问题(GPE2)的最优解.

2 算 法

有了以上的准备,下面给出本文的算法步骤如下:

(1)选取初始值x0∈Rn,λ0,σ0＞0,B0=I,置k:=0;

(2)计算 Ci(xk),▽Ci(xk),▽xL(xk,λk,σ);

(3)由式(3)和式(4)计算出 △λk和 △xk;

(4)若 △xk=0,则xk为问题(GPE2)的 K-T点,停;

(5)求解 ∂k为(1,…)中满足下式,

的最大值;

(6)修正罚因子σk为,其中,δ和ζ是正常数,rk= ‖λk‖;

3 收敛性证明

证明 (1)充分性.

若 △xk=0,则由式(2)可得到,

即,

故 xk为问题(GPE2)的 K-T点.

(2)必要性.

因为 xk,λk为问题(GPE2)的 K-T点,所以,

又,

我们把 △λk=0代入式(3),可以得到,

因为我们总是假设 ▽C(xk)是行满秩的,所以有,△xk=0.

因此,△xk为L(xk,λk,σk)下降方向.

引理2 若算法产生的数列{xk}有聚点,则存在k＊,当k＞ k＊时,σk≡σk＊≜σ＊.

证明 采用反证法.

如果上式不成立,则有σk→∞(k→∞),由式(6)知,σk= rk+ζ,即,σk= ‖λk‖∞+ζ,从而‖λk‖∞→∞(k→∞),则有{xk}无界.这与假设{xk}有聚点矛盾,故引理2成立.

引理3 当 △xk≠0时,函数L(xk,λk,σk)为一单调下降函数.

证明 当 △xk≠0时,由定理2,▽L(xk,λk, σk)T△x＊＜0.因此,由式(6),

再由σk的定义及引理2,引理3显然成立.

定理3 若算法产生的点列{xk}为一无穷点列,则{xk}的任一聚点x＊都是问题(GPE2)的 K-T点.

证明 设存在无穷子集K,使k∈K,xk→x＊.定义,

显然,由Ci(x),i=0,1,…,m的一阶连续可微性,有,

由引理3知,L(xk,λk,σk)单调下降.

故由xk→x＊(k∈K)知,

假设 △x＊≠0,则在 x＊处有,▽L(x＊,λ＊, σ＊)T△x＊＜0.从而,由L(x,λ,σ)的凸性及单调下降知,当k∈K,k充分大时,进而有,

式中,∂＊=max{∂k|k∈K,k→∞},由算法第5步,一定有 ∂＊＞0,从而得出矛盾.因此,△x＊=0,则此定理成立.

[1]Fletcher R.An Ideal Penalty Function for Constrained Optimization[J].J Applied Mathematics,1975,15(3):319-342.

[2]Di Pillo G,Grippo L.A New Augmented Lagrangian Function for Inequality Constraints in Nonlinear Programming Problems[J].J Optim Theory Appl,1982,36(4):495-519.

[3]Di Pillo G,Grippo L.A New Class of Augmented Lagrangians in Nonlinear Programming[J].SIAM J Control Optim,1979,17 (5):618-628.

[4]Di Pillo G,Lucidi S.An Augmented Lagrangian Function with Improved Exactness Properties[J].SIAM J Optim,2001,12(2): 376-406.

[5]Di Pillo G,Lucidi S.On Exact Augmented Lagrangian Functions in Nonlinearprogramming[C]//Nonlinear Optimization and Applications.NewY ork:Plenum Press,1996:85-100.

[6]Lucidi S.New Results on A Class of Exact Lagrangian Functions [J].J Optim Theory Appl.1988,58(2):259-282.

[7]王秀国,薛 毅.基于增广Lagrange函数的RQP方法[J].计算数学,2003,25(4):393-406.

[8]苏 洲.约束变尺度法应用研究[J].河海大学机械学院学报,1996,10(4):1-5.