基于Laplace变换的干气密封轴向自由振动与强迫振动解析研究
2023-01-09滕黎明江锦波彭旭东李纪云
滕黎明, 江锦波, 彭旭东, 陈 源,2, 李纪云
(1.浙江工业大学 机械工程学院,杭州 310014;2.中国计量大学 机电工程学院,杭州 310018)
干气密封因具有低泄漏、低功耗和长寿命等性能优势而在中高速旋转机械中得到广泛应用,不过在实际运行中,由于制造装配误差、转轴振动、工况波动、端面变形及密封端面气腔等存在,密封环将不可避免地会发生振动,进而造成密封间隙的波动,甚至会出现密封端面严重磨损或过量泄漏等失效发生。随着压缩机、风机、离心泵等高速旋转机械进一步提速,对干气密封的动态稳定性提出了更高的要求,但针对干气密封动态性能优化设计的指导文件国内目前还相对匮乏。因此,提供准确的干气密封振动特性计算公式和方法对保障我国石化、能源及制药等领域关键设备的可靠性和安全性具有重要战略意义。
近几十年来,许多学者针对干气密封在受到外界瞬时或持续激励下的浮动环自由振动和强迫振动特性展开研究。干气密封振动特性的求解主要有两种方法,一种是先基于摄动法[1-2]、阶跃法[3-4]或直接频率响应法[5]等线性化方法获得气膜动特性系数,后代入运动方程中获得补偿环振动响应;另一种是联立求解瞬态雷诺方程和运动方程[6-10],直接获得补偿环的振动响应。线性化方法因在微幅振动下具有较高的计算精度和计算效率[11-12],故在干气密封振动特性分析研究中得到较高认可。
在采用线性化方法分析干气密封振动特性时,目前主要基于数值法获得浮动环的振动特性[13-15],进而研究工况参数、激励参数、气膜参数和结构参数对密封环振动特性的影响。数值法研究的不足在于无法直观地获得各影响参数之间的关联关系及其影响规律,研究结论的适用性也受限于所选取计算参数的范围,而解析法则更为直观,且可获得具有更大范围适用性的研究结论。通过Laplace变换可将时域内的振动微分方程转换为频域内的代数方程,并在求得传递函数后作Laplace逆变换返回为时域问题,进而可求得满足初始条件的振动微分方程解析解,目前该法已被用于求解密封动特性的解析解。Ruan等[16-18]基于拉氏变换研究了螺旋槽干气密封和动静压干气密封在受到轴向和角向激励下的密封环振动特性;Miller等[19]基于Laplace变换和Fourier变换开展了螺旋槽干气密封动态特性的半解析求解;张强等[20]将拉氏变换和泰勒展开引入到蜂窝密封动力特性系数的计算中,显著提高了计算效率。不过,上述工作并未明确给出密封环的自由振动和强迫振动响应位移解析表达式,且对于不同特征方程根条件下的密封环振动位移解析解未能展开讨论。实际上,当密封的动态特征参数“阻尼-刚度-质量”三者处于不同数值关系时,其对应的干气密封轴向振动位移响应表达式各有不同。
不失一般性,本文以静环挠性安装(即静环为浮动环)干气密封为研究对象,在轴向振动特性求解几何和物理模型的基础上,基于Laplace变换推导了浮动环轴向自由振动和强迫振动响应的显式解析表达式,分析了浮动环质量、系统总刚度和系统总阻尼对干气密封轴向自振特性及过渡阶段响应最大振幅和调节时间的影响;推导获得了密封在轴向持续激励下稳定运行阶段的周期性扰动峰值显式表达式,研究了浮动环质量、激励频率、刚度和阻尼参数对密封振动周期峰的影响规律。研究结果为工程技术人员提供了可准确预测干气密封受扰后膜厚响应规律的计算公式,并以轴向强迫振动周期峰为优化目标,给出了各影响因素的优选范围,为密封系统力学元件特性参数之间的协同优化提供了理论指导。
1 干气密封轴向振动特性求解模型
1.1 物理和几何模型
典型的静环挠性安装干气密封结构及其运动学模型示意图,如图1所示。干气密封的主要结构包括固定安装于转轴(旋转角速度为Ω)上的动环及挠性安装于静环座上的浮动静环,动环和静环端面之间有一层厚度为hb的气膜隔开以实现非接触运行,静环与静环座之间设有刚度为ks的支撑弹簧和阻尼为cs的辅助密封圈,用以保证静环的浮动性和追随性。在动环端面上,从槽根半径rg至外径ro处开设有数量为Ng、深度为hg的对数螺旋槽,靠近内径ri处设有不开槽的密封坝,螺旋槽的螺旋角为β,槽区周向开槽宽度与密封堰宽度相等。气膜可看成是具有一定刚度kzz和阻尼czz的“弹簧-阻尼”结构,浮动静环在气膜、弹簧和辅助密封圈的共同作用下实现对动环轴向激励的响应,保持对动环扰动的追随。在本文分析中,仅考虑轴向扰动,而忽略角向扰动;在强迫振动分析中,仅考虑动环受到轴向正弦激励zr=Arzsinωt,其中:Arz为激励振幅;ω为激励频率。
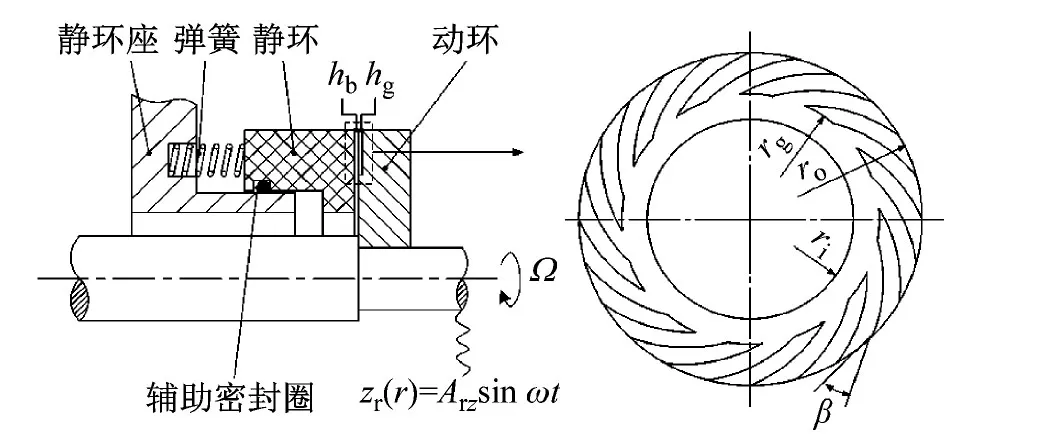
(a) 几何结构模型

(b) 运动学模型图1 静环挠性安装干气密封结构及运动学模型示意图Fig.1 Schematic diagram of the geometric structure and kinematic model of the flexibly mounted stator DGS
1.2 数学模型
1.2.1 轴向自由振动模型
干气密封浮动静环的轴向振动可分两种情况讨论:一是受到任意瞬时激励的轴向自由振动;二是受到轴向持续激励的强迫振动。仅考虑干气密封浮动静环的轴向激励,忽略角向激励对轴向响应的影响,则浮动静环轴向自由振动运动方程为
(1)
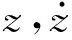
根据式(1),静环加速度可表示为
(2)
式中:相对阻尼系数cm=c/m;相对刚度系数km=k/m。
对式(2)两端同时作Laplace变换,将浮动环振动特性的时域问题转换为频域问题,利用第二微分性质可得
-cm[sZ(s)-z(0)]-kmZ(s)
(3)
由式(3)可得传递函数Z(s)为
(4)
利用部分分式法对式(4)进行Laplace逆变换,首先需将传递函数转化为部分分式表达。令式(4)分母为零可得系统特征方程为
s2+cms+km=0
(5)
根据式(5)特征根的分布,可分为下列3种情况讨论。
(1) 特征方程有一对共轭复根
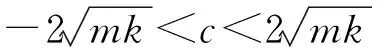
(6)
传递函数式(4)可表示为
(7)
式中,k1,k2为待定系数,且k1,k2共轭,也即
k1,2=α±βi
(8)
式(7)的逆Laplace变换可表示为
z(t)=k1eλ1t+k2eλ2t=
(9)
根据Euler公式,式(9)中的复指数可化为三角函数形式,并将式(8)代入可得
(10)
待定系数k1,2可根据式(11)求解
ki=[(s-λi)Z(s)]s=λi
(11)
将式(4)、式(6)代入式(11)可得
(12)
则式(1)的解为
(13)
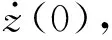
进一步,式(13)可化为
z(t)=A(t)sin(ωdt+φ)
(14)
式中:A(t)为随时间变化的振幅,在“位移-时间”图中z=±A(t)即振荡包络线;ωd为阻尼振荡频率;φ为相位角
(15)
(16)
(17)
(2) 特征方程有两个不等实根
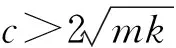
(18)
传递函数式(4)的部分分式表达形式与式(7)相同,其中的待定系数k1,2利用式(11)确定。
(19)
由式(9)可得此时式(1)的解为
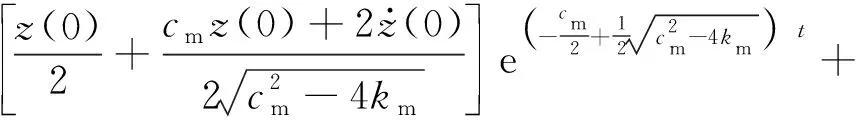
(20)
(3) 特征方程有两个相等实根
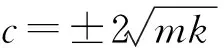
(21)
传递函数式(4)可表示为
(22)
式中,k11,k12为待定系数。
式(22)的逆Laplace变换可表达为
z(t)=eλt(k12+k11t)
(23)
待定系数k11,k12可根据式(24)求解
(24)
将式(4)、式(21)代入式(24)可得
(25)
则式(1)的解为
(26)
1.2.2 轴向强迫振动模型
引入轴系跳动引起的轴向激励运动zr,不失分析一般性的前提下,假定其为式(27)所示的简谐周期激励
zr(t)=Arzsinωt
(27)
在式(27)所示简谐激励作用下,浮动静环的轴向强迫振动运动方程为
(28)
式中:F1=kzzArz;F2=czzωArz。令f1=F1/m,f2=F2/m。
静环加速度可表示为
(29)
对式(29)等号两端同时作Laplace变换,并利用第二微分性质有
-cm[sZ(s)-z(0)]-kmZ(s)+
(30)
由式(30)可得
(31)
传递函数式(31)的部分分式形式可写作
(32)
式中,k1,k2,k3,k4为待定系数。
由式(31)与式(32)恒等可得
(33)
解得各待定系数为
(34)
(35)
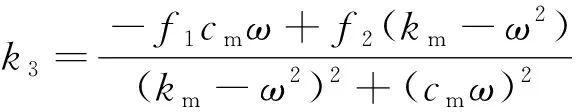
(36)
(37)
由第一线性性质,式(32)的Laplace逆变换可表达为
(38)
式中,L-1{Z1(s)}的求解方法可类比轴向自由振动,分为3种情况讨论。
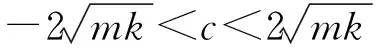
Z1(s)的部分分式形式为
(39)
其中,特征根λ1,2如式(6)所示,待定系数A1,2如式(40)所示
(40)
则Z1(s)的逆Laplace变换为
(41)
由式(34)~式(38)、式(41),归并化简可得浮动静环振动响应为:
z(t)=z0(t)+z1(t)+z2(t)
(42)
式中:z0(t)为初始条件响应;z1(t)为自由伴随振动;z2(t)为强迫响应;具体表达式如下
(43)
(44)
(45)
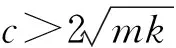
Z1(s)的部分分式表达形式与式(39)相同,其中的特征根λ1,2如式(18)所示,待定系数A1,2如式(46)所示
(46)
则Z1(s)的逆Laplace变换为
(47)
由式(34)~式(38)、式(47)可得此时浮环振动响应表达形式与式(42)相同。其中强迫响应z2(t)不变,如式(45)所示;而初始条件响应z0(t)与自由伴随振动z1(t)分别为
(48)
(49)
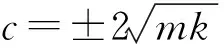
Z1(s)的部分分式形式为
(50)
式中,特征根λ如式(21)所示,待定系数A11,A12如式(51)所示
(51)
则Z1(s)的逆Laplace变换为
(52)
由式(34)~式(38)、式(52)可得此时浮环振动响应表达形式与式(42)相同。其中强迫响应z2(t)不变,如式(45)所示;而初始条件响应z0(t)与自由伴随振动z1(t)分别为
(53)
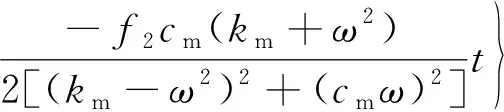
(54)
2 结果讨论与分析
基于第1章推导的静环挠性安装干气密封轴向自由振动和强迫振动响应解析表达式,研究了密封刚度和阻尼、激励频率、浮动环质量等相关参数对干气密封轴向自由振动和强迫振动特性的影响。在下述的算例中,除特别说明外,各参数的缺省值根据Ruan的研究确定:也即密封环内径ri=30 mm,外径ro=42 mm,槽根半径rg=33.6 mm,螺旋角β=20°,槽深hg=5 μm,槽数Ng=12;浮动环质量m=0.2 kg,轴向气膜刚度kzz=1.281 7×108N/m,轴向气膜阻尼czz=1.739 9×104N·s/m,弹簧刚度ks=1×107N/m,辅助密封阻尼cs=1×103N·s/m,激励频率ω=376 rad/s。
2.1 干气密封轴向自振稳定性参数影响
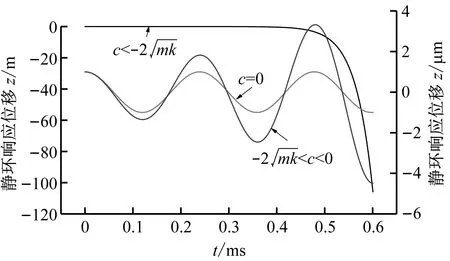
干气密封可看成是一个由“弹簧-阻尼-质量”组成的振子系统,刚度、阻尼和质量是影响密封自振稳定性的3个关键参数。由于在轴向自由振动过程中没有固定动环的持续激励,故浮动环响应位移即为气膜厚度的变化,可通过浮动静环响应位移曲线的振幅、频率和响应时间来判断密封轴向自振稳定性。一般来说,响应位移曲线的振幅越小,意味着阻尼程度越强;响应时间越短,意味着响应速度越快,对应的密封系统自振稳定性越好。
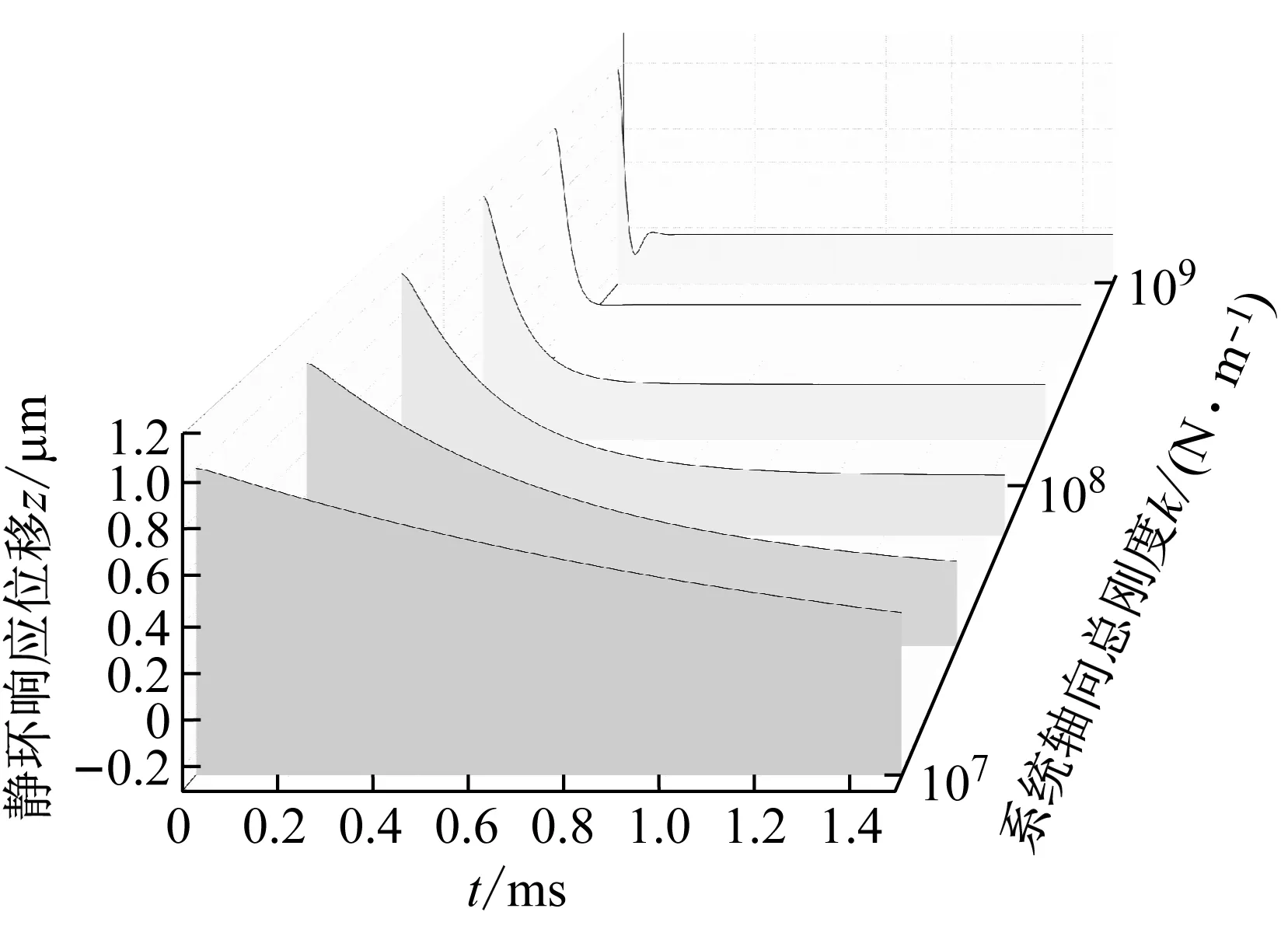
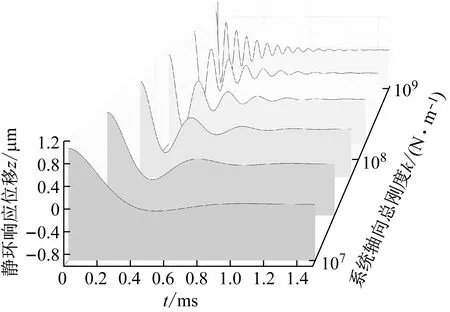
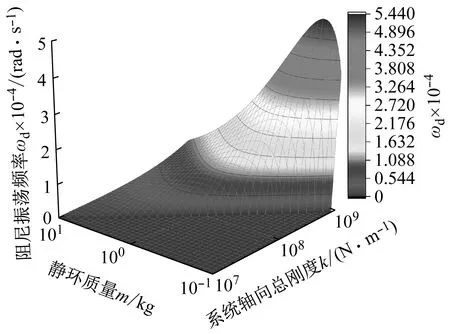
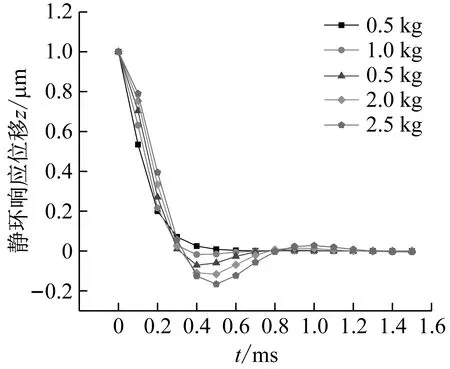
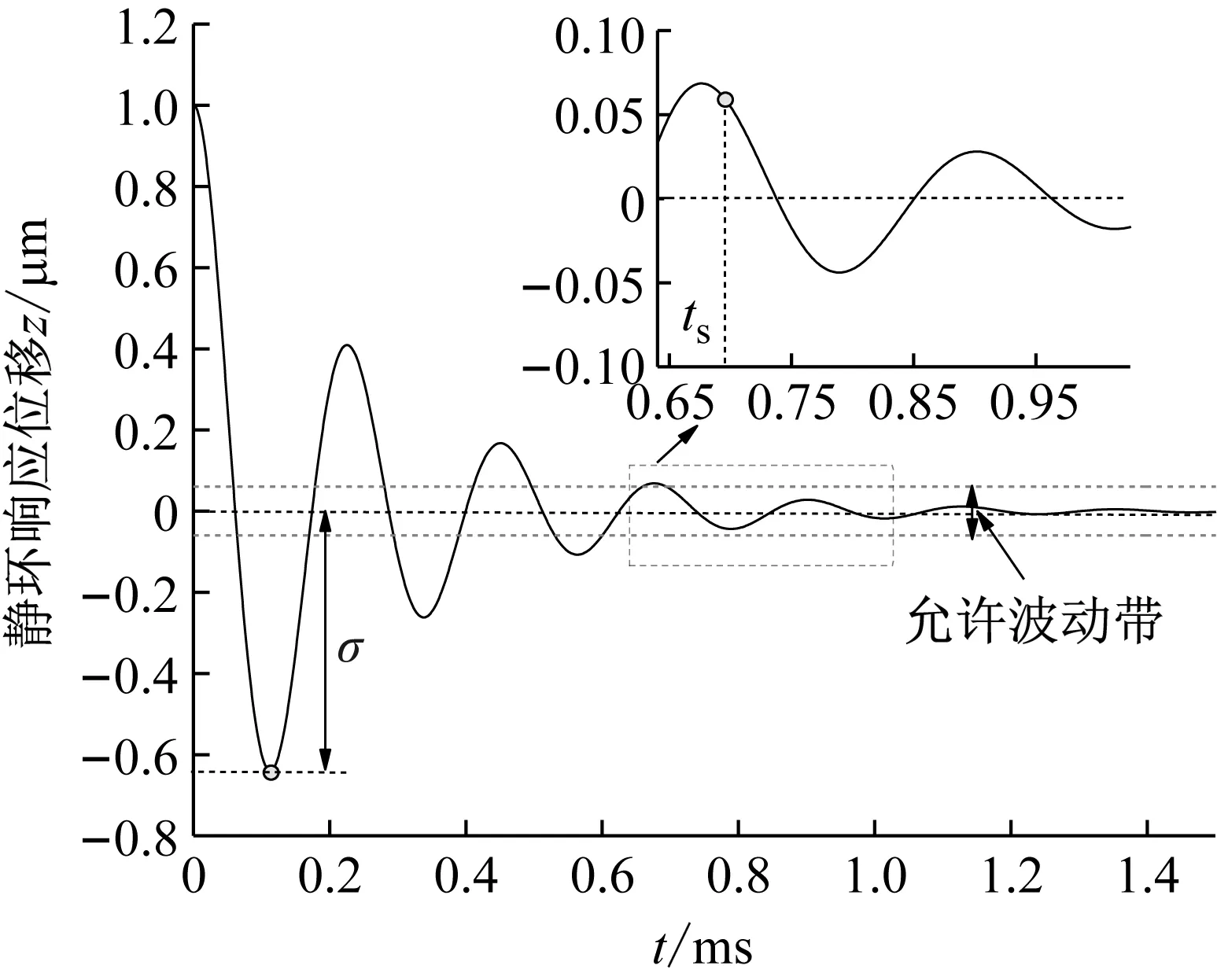
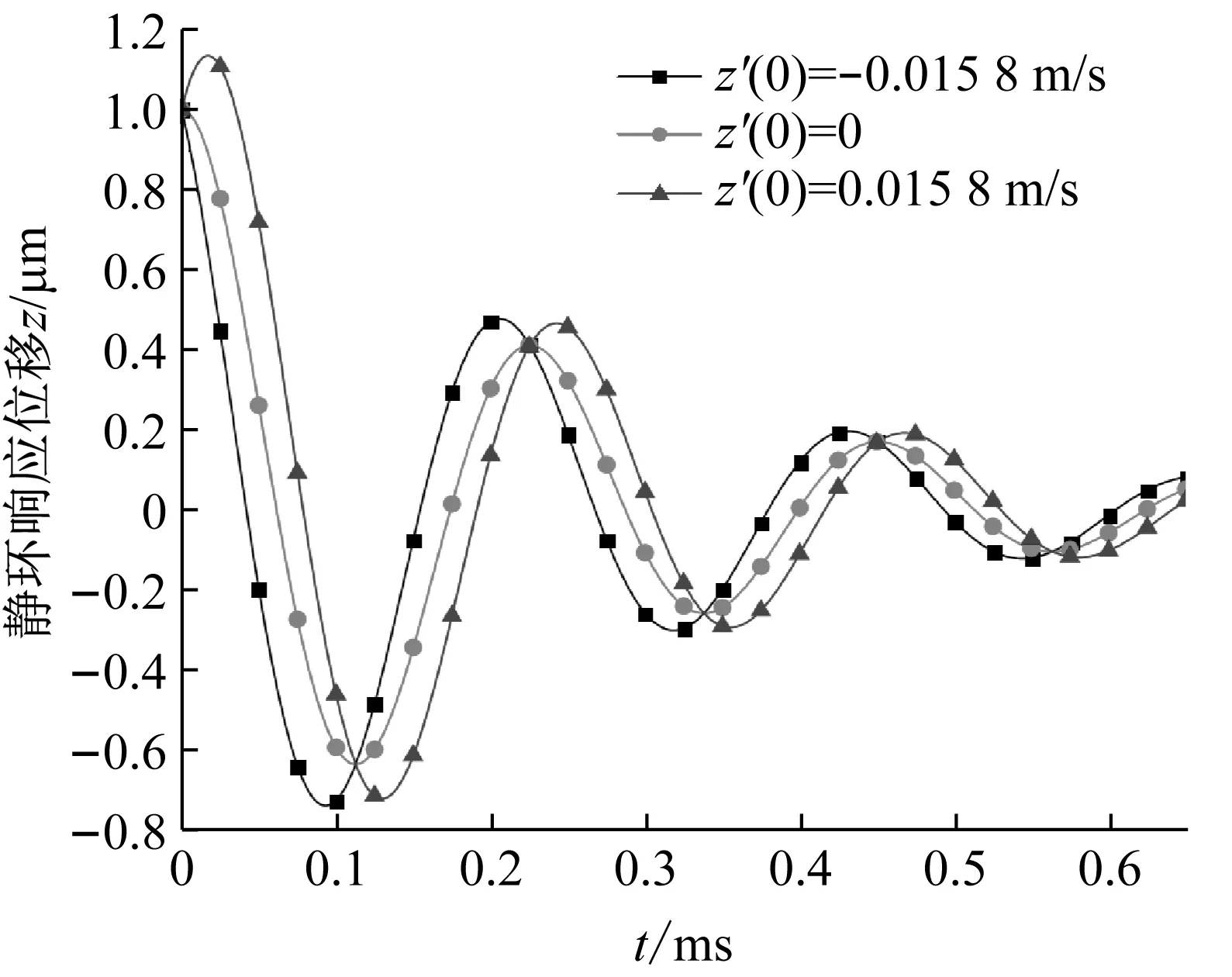
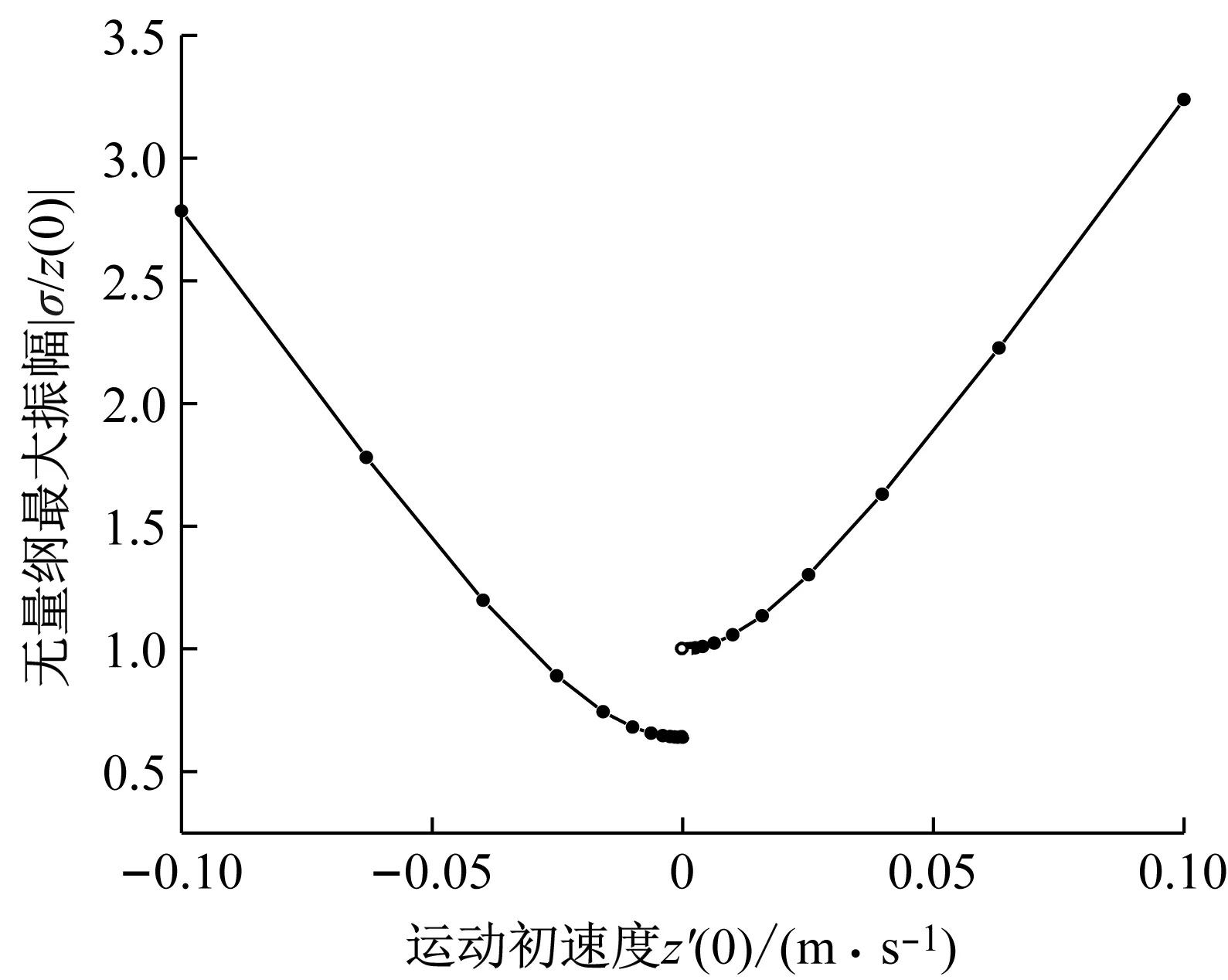
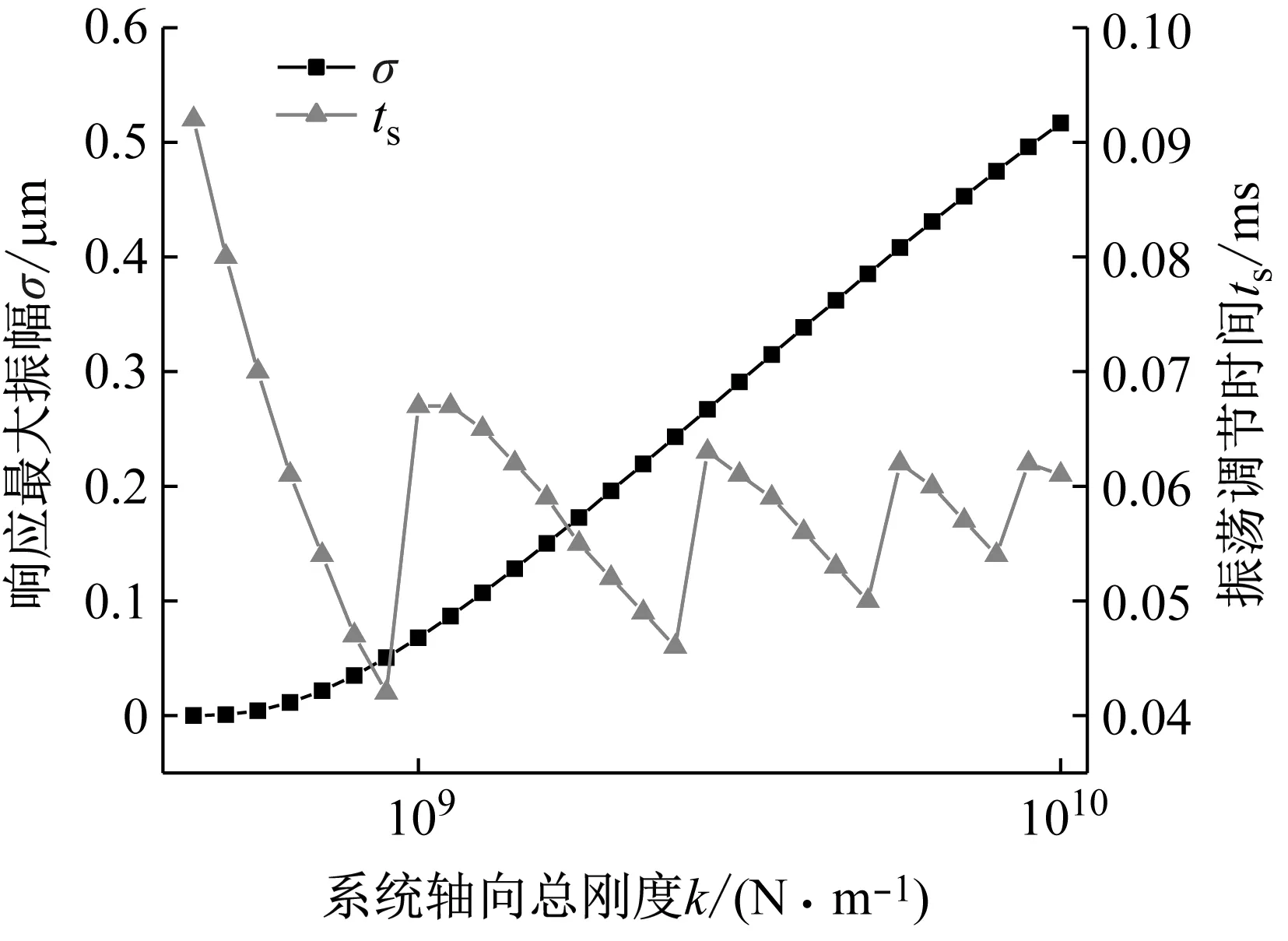
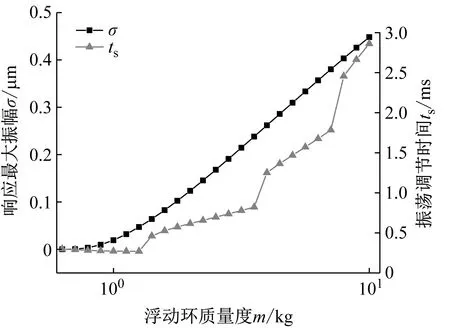
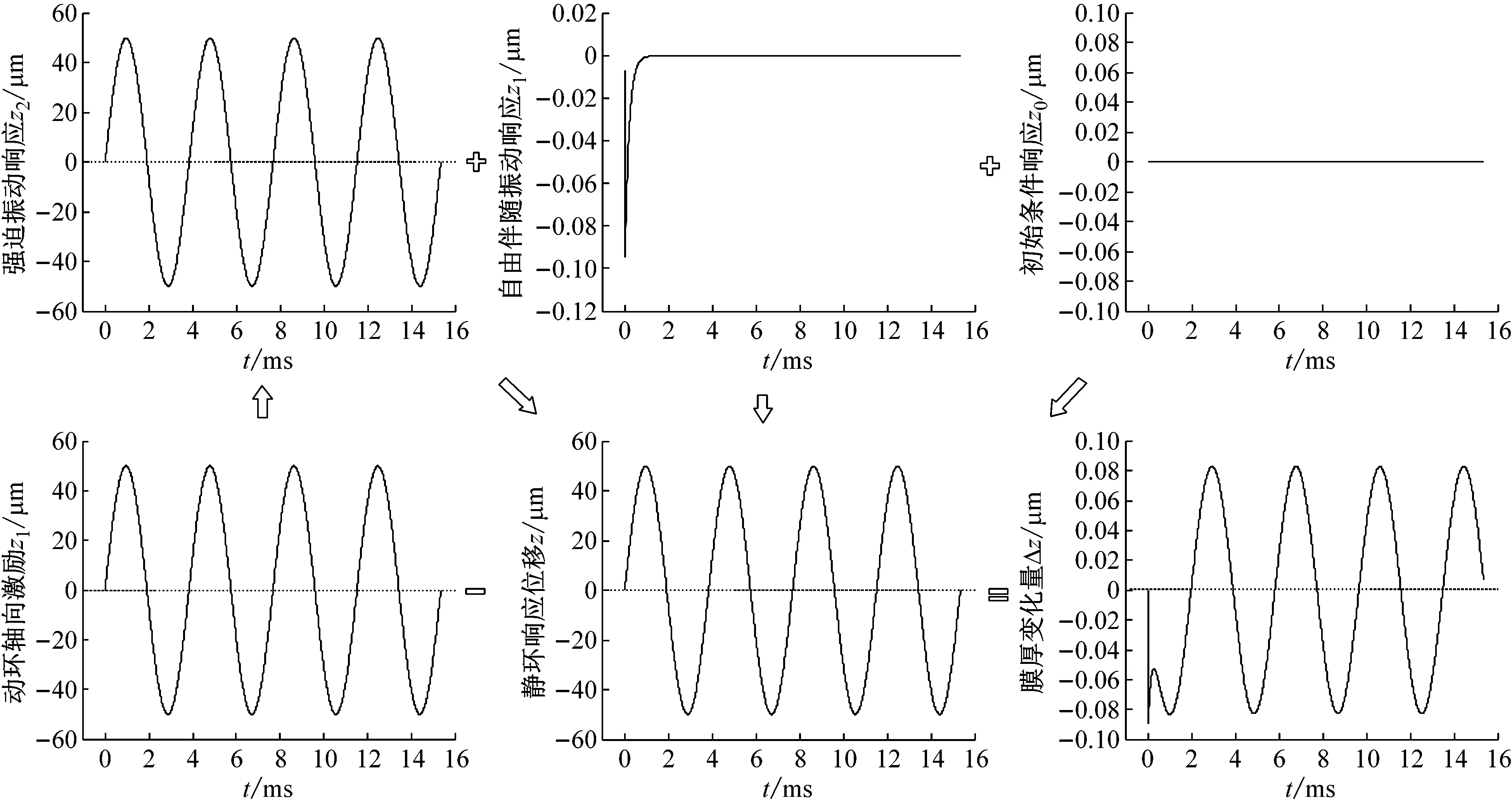
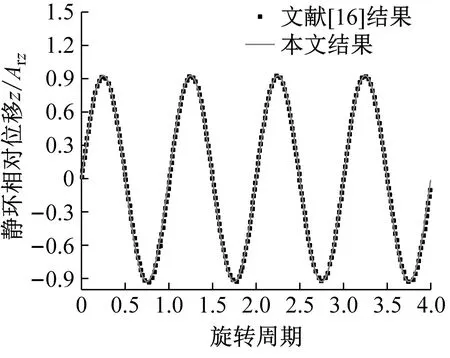
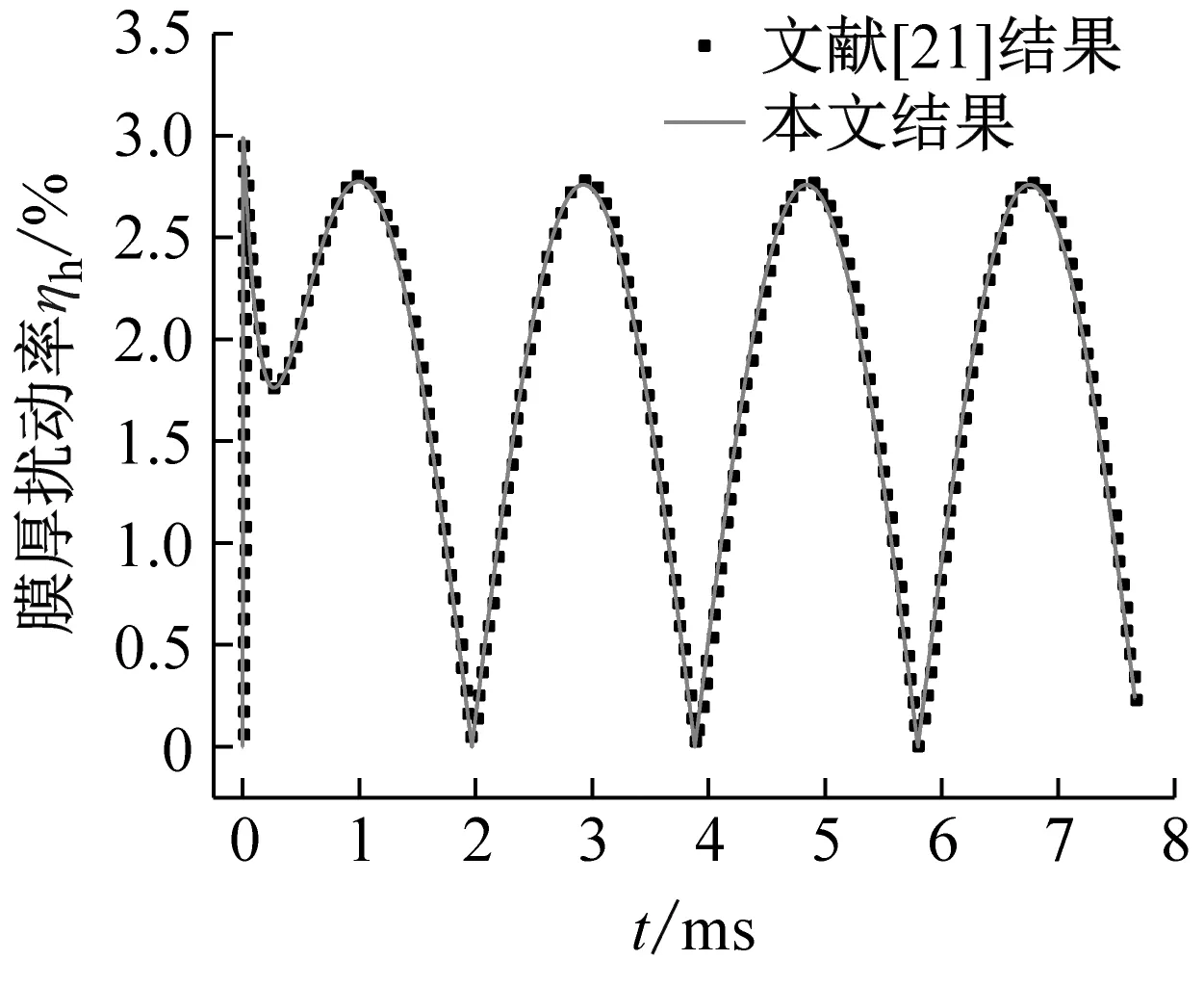
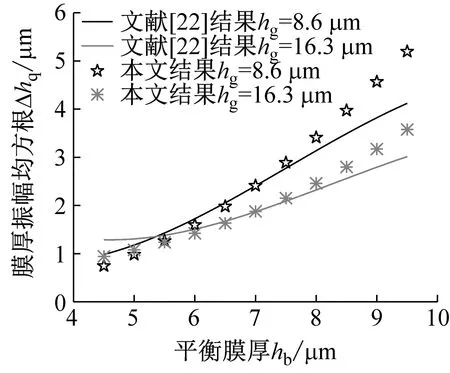
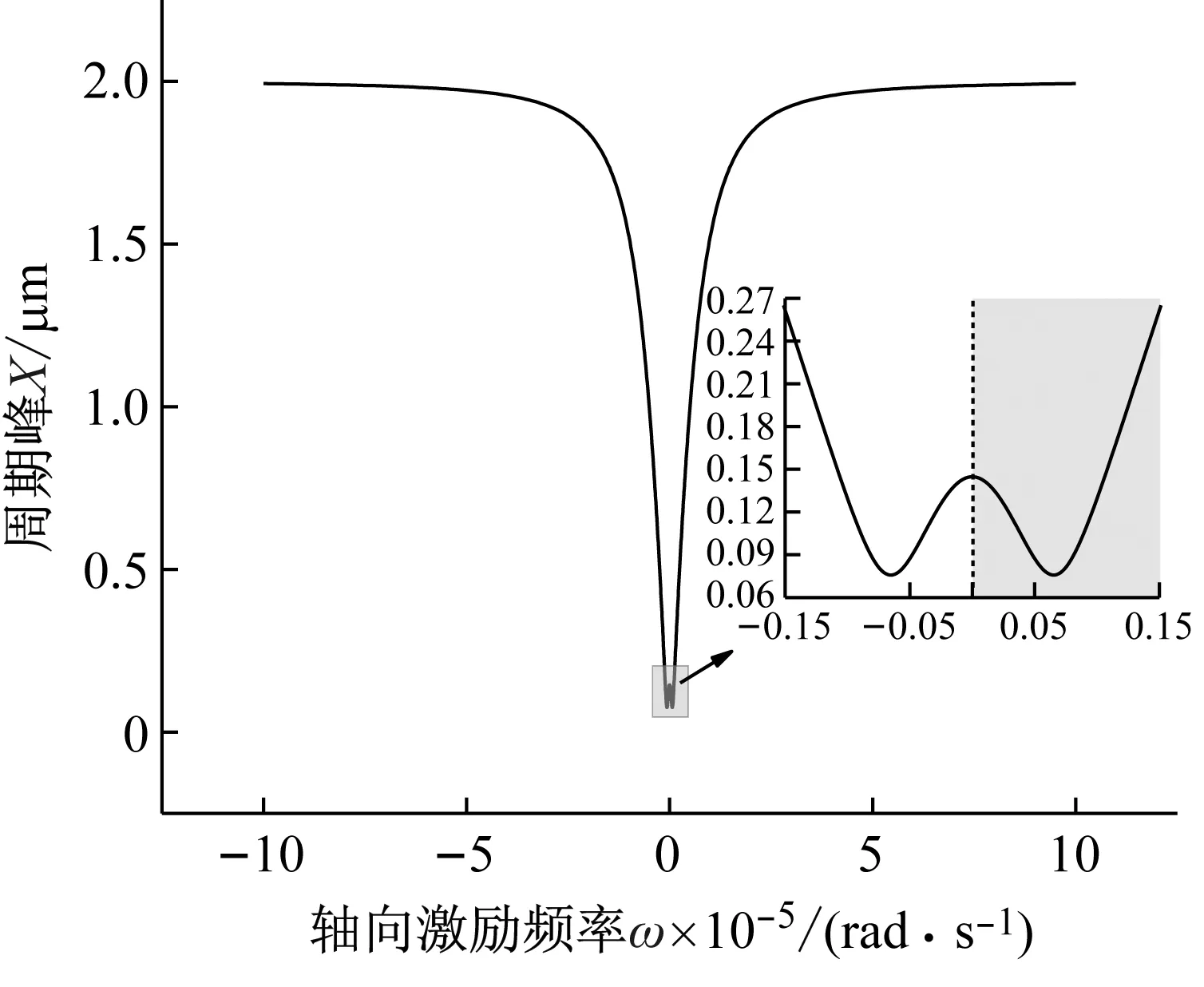
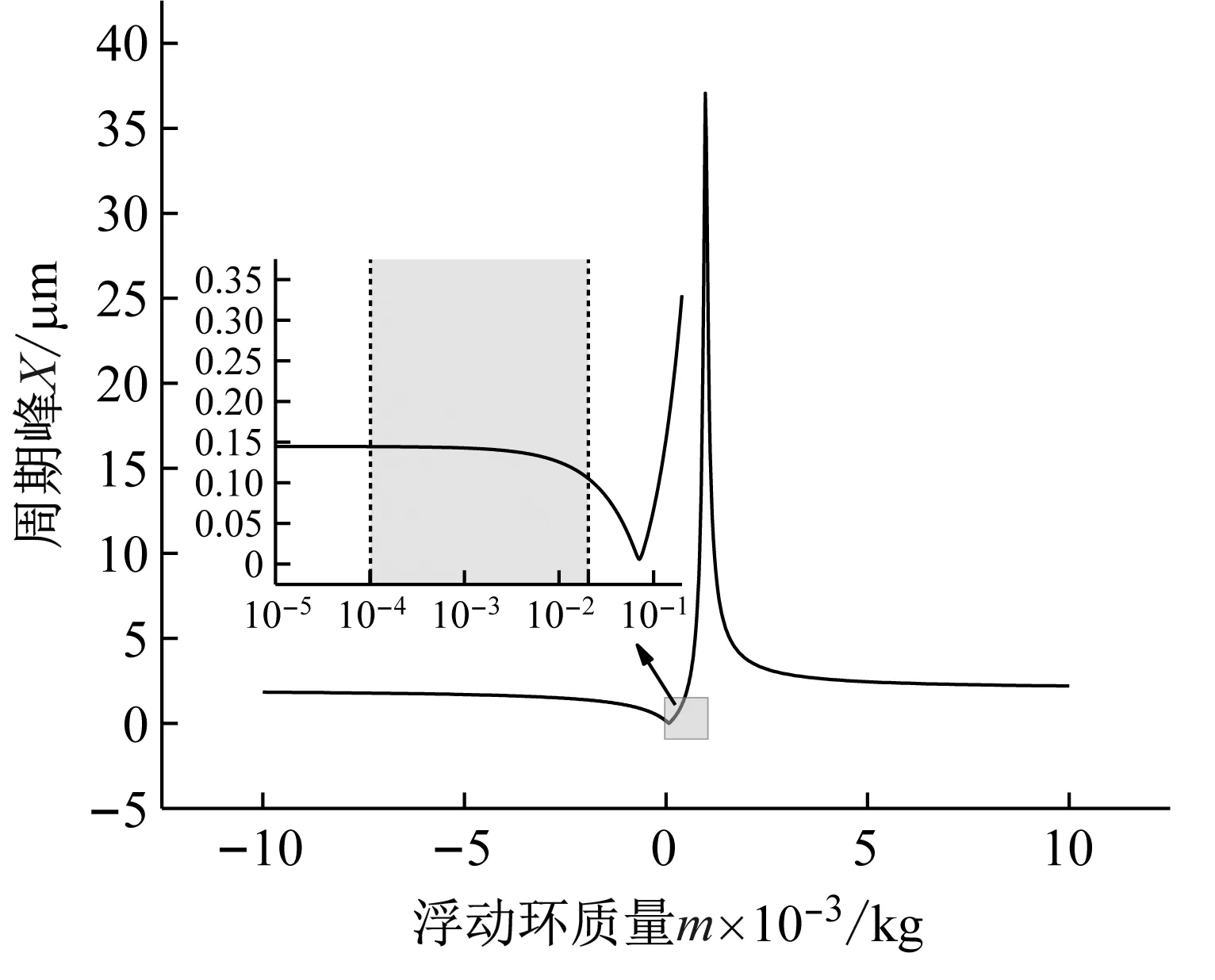
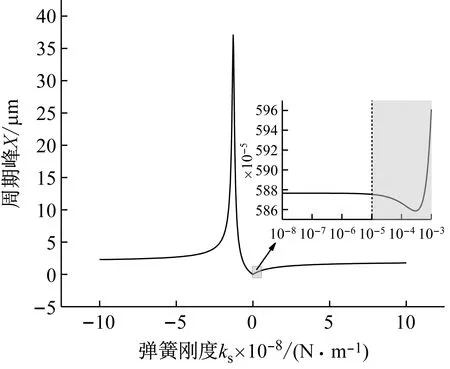
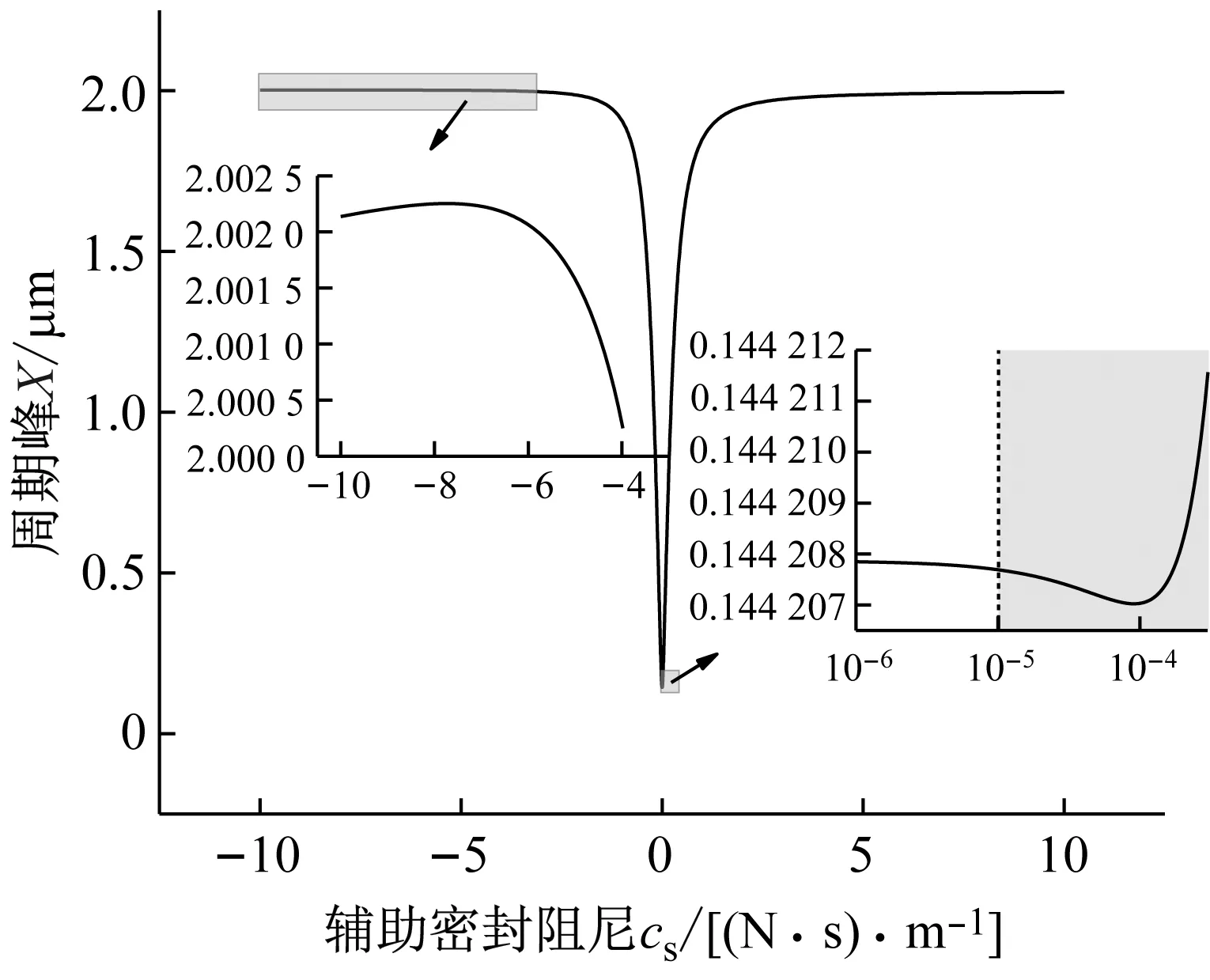
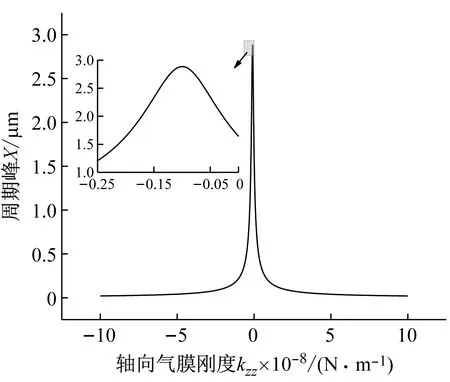
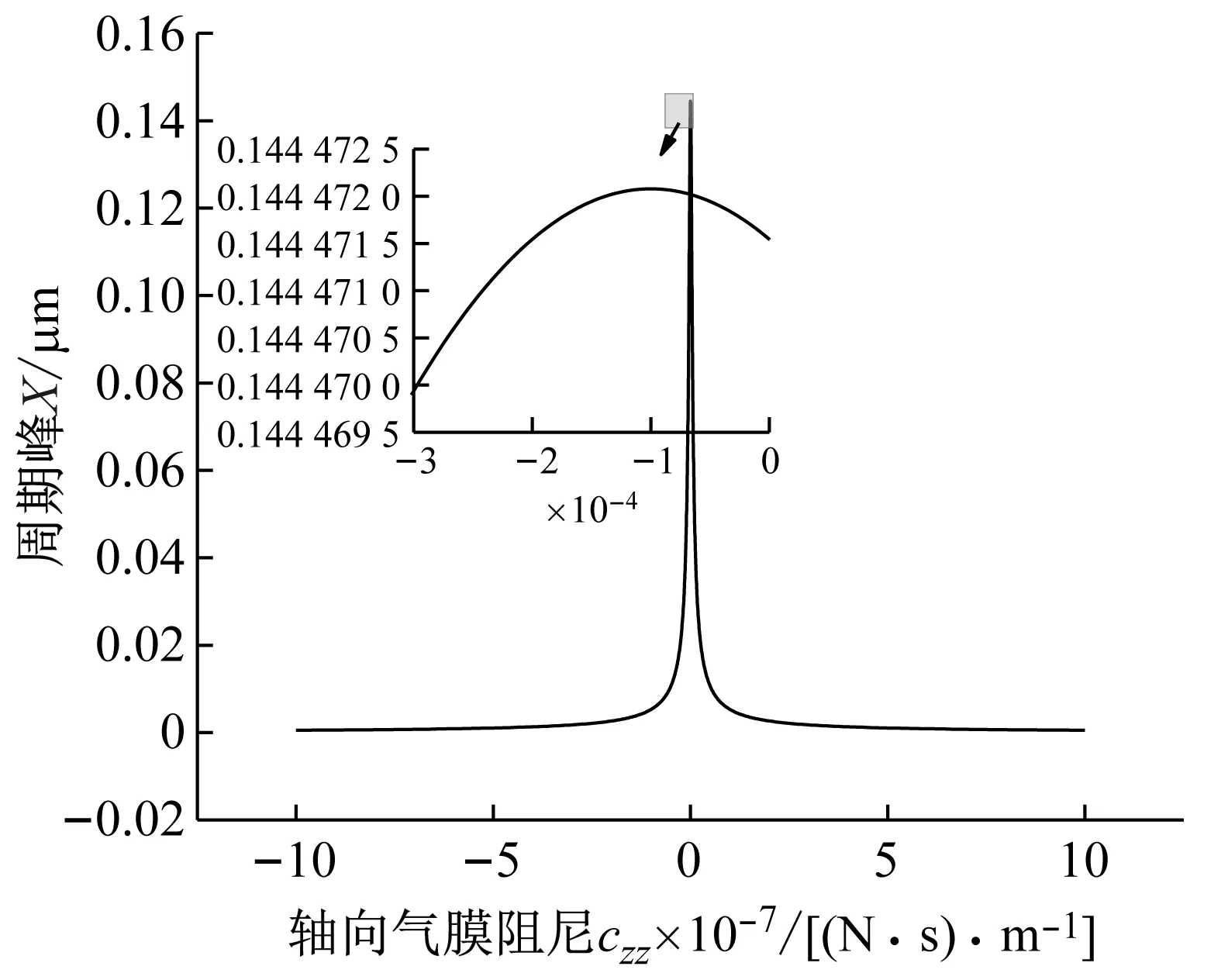
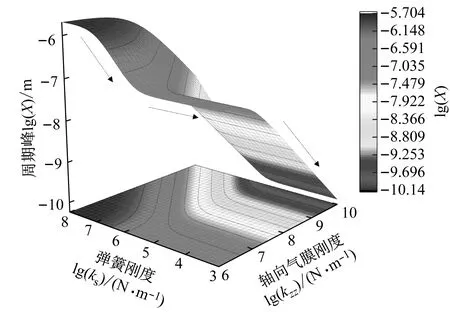
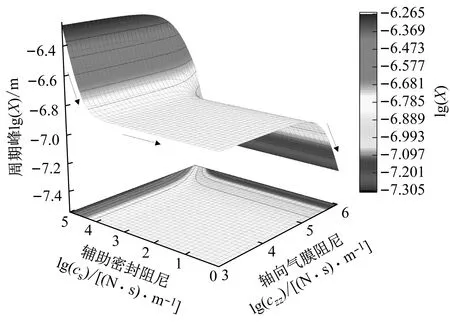
系统总阻尼对干气密封静环响应位移的影响,如图2所示。可以看出,总阻尼c对密封系统的稳定状态影响显著,当总阻尼c>0时处于稳定状态(见图2(a)),当c≤0时处于不稳定状态(见图2(b))。当处于c>2(mk)1/2的过阻尼状态时,静环在初始位移扰动下的响应曲线单调衰减,不发生振荡;当处于c=2(mk)1/2的临界阻尼状态时,静环的响应曲线形式与过阻尼状态接近,也为一单调曲线,但响应时间比过阻尼状态显著缩短;当处于0 (a) c>0 (b) c≤0图2 系统总阻尼对静环响应位移的影响Fig.2 Effect of total damping of system on displacement response of stator 当c=0时静环响应曲线为无阻尼等幅振荡,一般将其与负阻尼系统一同视为不稳定状态。当c<0时为负阻尼系统,系统时间响应关系式中会出现正指数,初始位移扰动下的静环响应是一发散的响应过程,静环响应位移不能达到稳定状态,随着时间的推移而逐渐发散。不同阻尼值时负阻尼系统的响应曲线也有所区别,当阻尼绝对值较小时(-2(mk)1/2 对于理想的弹簧振子(系统阻尼为零),若将其移开平衡位置,系统会在平衡位置附近持续振动,振幅与振动能量均保持不变(见图2(b)),这是因为弹性元件在振动过程中能够储存势能,而物体惯性则储存动能,二者可以相互转换。但对于实际干气密封振动系统,端面间气膜存在轴向阻尼,且受工况条件与端面结构的影响,其阻尼值可能为正也可能为负。考虑系统阻尼后,系统的机械能便不再守恒,损失的能量用于克服阻尼力做功,故系统轴向总阻尼c反映了系统耗散振动能量的能力。当c超过临界阻尼时,系统偏离平衡位置后会逐渐回复到平衡位置且受强阻尼力的作用系统不会发生振动,但阻尼不宜过大否则类似于刚性连接,系统趋于平衡的时间过长。若c不够大,阻尼力不足以阻止振动越过平衡位置,系统将作振幅逐渐衰减的周期性振动,且c越小振动过程中的振幅越大(见图2(a))。当c<0时,阻尼力与系统振动相对速度的方向不再相反,而是相同,且速度越大阻尼力也越大。此时,系统内由于负阻尼形成了补充振动能量的能源,系统若偏离平衡位置会自发地产生和维持振动,不能达到稳定状态。 系统总刚度对静环响应位移的影响,如图3所示。可以看出,系统轴向总刚度k的取值不会改变系统的稳定状态,而会影响系统响应曲线的振幅、频率和响应时间。当系统总阻尼较大时(c=1.584 9×104N·s/m),适当提高轴向总刚度k,可使系统由过阻尼状态过渡到临界阻尼或欠阻尼状态,有利于缩短系统响应时间,提高系统稳定性;而在系统总阻尼较小时(c=1.584 9×103N·s/m),增大轴向总刚度k,过渡过程的振幅和频率也会加大,不利于系统稳定。 (a) 较大系统阻尼 (b) 较小系统阻尼图3 系统总刚度对静环响应位移的影响Fig.3 Effect of total stiffness of system on displacement response of stator 正如前文所言,振动实际是动能和势能的转换,机械系统必须同时具有惯性与弹性,这样才能有动能和势能,而惯性取决于质量,弹性取决于刚度。惯性大,动能状态的变化要难;刚度小,势能状态的变化要难。给定了系统的质量与刚度后,振动过程中能量的转换速率就随之确定,也即无阻尼自然振荡频率ωn(或称为系统固有频率,ωn=(k/m)1/2)。故提高系统轴向总刚度k能显著增加欠阻尼系统过渡过程振荡的频率。而k对系统响应曲线振幅产生影响主要是由于改变了系统的阻尼程度。在系统轴向总阻尼c一定的情况下,调节k可以改变弹性恢复力与阻尼力的相对大小。当系统阻尼力较大时,提高弹性恢复力以有效克服运动阻碍可使系统快速回到平衡位置(见图3(a))。而当系统阻尼力较小时,提高弹性恢复力会增加系统储存的振动能量,增大过渡过程振荡的强度(见图3(b))。 浮动环质量m对阻尼振荡频率和静环响应位移的影响,如图4所示。浮动环质量m也主要是影响静环响应曲线的振幅、频率和响应时间,而不改变系统的稳定状态。浮动环质量m的增大可使系统由过阻尼状态转变为欠阻尼状态。由式(16)可知,在欠阻尼状态下增加轴向总刚度k,阻尼振荡频率ωd单调增加,而质量对阻尼振荡频率的影响则有所不同。令ωd对m的偏导数为零可得m=0.5c2/k。将m=0.5c2/k代入式(3)可得ωd=k/c。故浮动环质量m存在一极值点0.5c2/k使ωd取得最大值k/c,此时响应曲线从零时刻至首次达到稳态值的时间最短。如图4(a)所示,超过m的极值点后,若再继续增加浮动环质量,则系统振动的振幅增大,阻尼振荡频率减小,即阻尼程度和响应速度同时下降,动态性能指标劣化,自振稳定性降低。 (a) 阻尼振荡频率 (b) 静环响应位移图4 浮动环质量对阻尼振荡频率和静环响应位移的影响Fig.4 Influence of floating ring mass on damping oscillation frequency and stator displacement response 对于过阻尼或临界阻尼系统,在初始位移扰动下,浮动环在进入稳定状态之前并不存在振荡的过渡阶段,而在欠阻尼系统中则存在呈衰减振荡的过渡阶段,有必要研究干气密封在过渡振荡阶段的自振稳定性及其影响因素。由2.1节分析可知,系统的阻尼程度和响应速度一般难以同时达到最佳状态,为定量地评价欠阻尼系统中轴向总刚度k与浮动环质量m对干气密封浮动环自由振动过渡阶段动态性能的影响,定义了欠阻尼系统过渡阶段的响应最大振幅σ与振荡调节时间ts两个参数。 干气密封浮动环自振过渡阶段响应最大振幅和振荡调节时间的定义示意图(k=1.584 9×108N/m,c=1.584 9×103N·s/m),如图5所示。响应最大振幅σ为过渡振荡阶段浮动环运动后出现的首个响应位移峰值的绝对值,σ值越小,意味着密封端面发生碰撞的几率就越低;振荡调节时间ts为静环响应曲线达到并保持在允许波动带范围内所需的最短时间,ts值越小,意味着膜厚达到稳定状态的时间越短。 图5 干气密封浮动环响应最大振幅与调节时间定义Fig.5 Definition of maximum response amplitude and adjusting time of DGS floating ring response 为确保评价基准的统一,本文中允许波动带范围设为±Δ·hb,其中Δ为相对偏差,hb为平衡膜厚。根据式(14),当t≥ts时有 (55) 其中,a表示为 (56) 在响应最大振幅处,静环响应位移随时间的变化率为零,欠阻尼状态下令dz(t)/dt=0可得 A(t)ωdcos(ωdt+φ)=0 (57) 由A(t)恒为正,式(57)可进一步化为 sin(ωdt+φ+θ)=0 (58) 其中,阻尼角θ满足 (59) 欠阻尼状态下有0 由式(58)可得,浮动静环响应曲线的峰值时间tp为 (60) 将峰值时间tp代入z(t)可得该时刻的静环响应位移 z(tp)= (61) 静环响应的最大振幅σ即z(tp)的绝对值。 特别地,不考虑静环零时刻运动初速度时,则有 (62) 可见,若不计及静环零时刻的运动初速度,无量纲最大振幅|σ/z(0)|完全由系统阻尼特性所决定,而当静环具有轴向运动初速度时,无量纲最大振幅|σ/z(0)|还将受运动初始值的影响。运动初速度对静环响应位移和无量纲最大振幅的影响(k=1.584 9×108N/m,c=1.584 9×103N·s/m),如图6所示。如图6(b)所示,z′(0)=0为一左连续的跳跃间断点,这是运动初速度与初位移方向的差异所致。零初速度下,最大振幅出现在初位移方向的异侧,且由于阻尼作用,最大振幅小于初位移的绝对值。当运动初速度不为零且与初位移异向时,与零初速度的情况相同,最大振幅也出现在初位移方向的异侧,但随着运动初速度绝对值的增大,最大振幅逐渐增大,且相较于初位移,运动初速度对最大振幅起主导作用,最大振幅将逐渐超过初位移的绝对值。当运动初速度与初位移同向时,浮动环开始运动后其位移绝对值先逐渐增大至最大振幅位置,故最大振幅出现在初位移方向的同侧,且始终大于初位移的绝对值。在运动初速度z′(0)的绝对值相同时,由于运动初速度与初位移异向时的峰值时间tp相对同向时滞后,因此导致速度和位移异向时的最大振幅将始终小于两者同向时的状态,这也从侧面反映了阻尼对振荡的削弱作用。 (a) 静环响应位移 (b) 无量纲最大振幅图6 运动初速度对静环响应位移及最大振幅的影响Fig.6 Effect of initial velocity of motion on displacement and maximum amplitude of stator response 欠阻尼系统在初位移扰动下系统轴向总刚度k与浮动环质量m对过渡阶段特征参数的影响,如图7所示。其中相对偏差Δ=2%,平衡膜厚hb=3 μm。响应最大振幅σ随着k,m的增大都呈现单调递增的变化趋势且曲线连续,在较小的轴向总刚度和浮动环质量条件下能获得较小的响应振幅,这是由于对于系统的阻尼特性而言,k和m的影响规律相同。根据式(59)、式(62),系统轴向总阻尼一定时,k,m增大都将使阻尼角θ减小并趋近于π/2,同时响应曲线的振幅随tanθ的减小而增大。由式(55)可知,振荡调节时间ts是响应曲线振幅、阻尼振荡频率和允许波动带范围三者共同作用的结果,振荡调节时间随轴向总刚度和浮动环质量的增大呈现阶梯式非连续变化规律。随着k和m的增大,响应曲线振幅增大,若当前振荡周期的幅值超出了允许波动带范围,振荡调节时间ts就从当前周期跃变至下一周期,这是造成振荡调节时间非连续而呈阶梯状上升的主要原因。由图4可知:阻尼振荡频率随k的增大而单调递增,故在两个非连续跃变点之间k的增大会使得振荡调节时间逐渐减小;而阻尼振荡频率随m的增大呈现先增后减的变化规律,故m≤0.5c2/k时在两个非连续跃变点之间振荡调节时间随m增大而减小,当m>0.5c2/k时随m增大而增大,且增大的速率逐渐加快。值得注意的是,振荡调节时间在随刚度和质量增大的首个阶梯内都获得最小值,此时对应的响应最大振幅也较小,也即存在最佳的k和m使得系统兼具较好的阻尼特性和响应速度。 (a) 系统轴向总刚度 (b) 浮动环质量图7 零初速度下刚度与质量对最大振幅及调节时间的影响Fig.7 Effects of stiffness and mass on maximum amplitude and adjusting time at zero initial velocity 综上所述,在对干气密封轴向自由振动稳定性的影响方面,系统轴向总阻尼起着决定性作用,其数值的变化可使得系统在稳定态和非稳态之间转变;系统轴向总刚度和浮动环质量的改变不会影响系统的稳态状态,而会影响响应曲线的最大振幅和振荡调节时间。 相比于传统机械强迫振动研究中主要关注质量体的响应运动,干气密封强迫振动研究中更关注气膜厚度的变化量,因其是决定干气密封稳定性与密封性的关键。在受到固定动环的轴向激励后,干气密封膜厚变化量是静环响应位移和动环轴向激励之差。干气密封膜厚变化量与轴向强迫振动各参数的关联关系,如图8所示。根据式(42),浮动环的响应位移是初始条件响应z0、自由伴随振动z1和强迫响应z2三者相加的结果,其中强迫响应z2是频率等于动环激励频率的等幅振动;初始条件响应z0即为2.1节和2.2节中讨论的由初位移和初速度决定的轴向自由振动,为研究方便起见,取z0=0;自由伴随振动z1则只取决于系统本身的物理性质(m,k,c)和激励的大小和频率,而与运动初始条件无关。即使在零初始条件下,也有自由振动和强迫响应相伴发生。 图8 干气密封轴向强迫振动参数关系示意图Fig.8 Schematic diagram of the relationship between axial forced vibration parameters of DGS 为验证干气密封轴向强迫振动响应解析表达式推导的正确性,将本文解析推导获得的静环响应位移和膜厚变化量计算结果与文献[16]和文献[21]中的数值计算结果进行对比验证,结果如图9(a)、图9(b)所示。可以看出,本文所提供的解析表达式对于静环响应位移和膜厚变化量的计算与文献结果完全吻合。进一步,图9(c)示出了与文献[22]中膜厚振幅均方根试验数据的对比结果。可以看出,本文计算结果与试验值相近且趋势一致,但随着平衡膜厚的增大,发现计算偏差亦逐渐增大。这是由于膜厚扰动振幅较大时,气膜压力非线性凸显,此时将气膜视为具有一定线性化刚度kzz与阻尼czz的“弹簧-阻尼”结构将带来系统误差,但本文的方法仍可有效预测密封系统振动行为的趋势,验证了本文中相关解析推导过程的正确性。 (a) 静环相对位移 (b) 膜厚扰动率 (c) 膜厚振幅均方根图9 零初始条件下干气密封强迫振动响应正确性验证Fig.9 Verification of forced vibration response of DGS under zero initial condition 对于c>0的情况,无论受何种初始条件的作用,由于阻尼的存在,初始条件响应z0(t)与自由伴随振动z1(t)都会在极短的时间内衰减为零,静环持续的振动只有与外界激励有关的强迫响应z2(t)。 分别引入两个由外界激励以及系统本身物理性质决定的相位角θ1和θ2以简化式(45)的形式 (63) 则静环稳态响应振动方程式(45)可化为 (64) 由静环响应运动z(t)与轴向激励运动zr(t)相减可得膜厚变化量Δz(t)为 (65) 膜厚变化量Δz(t)的振幅X即为气膜在轴向激励zr作用下,长周期稳定运行阶段的周期轴向扰动峰值,简称为“周期峰”[23]。 (66) 式(65)可化为 (67) 由辅助角公式可得 (68) 将式(66)代入式(68),可得到静环挠性安装干气密封在受到轴向持续激励作用下膜厚变化的周期峰X为 (69) 周期峰X反映了干气密封在受到轴向持续激励下保持长周期动态稳定运行的能力,较小的周期峰可避免因膜厚过大或过小而造成的过量泄漏或端面碰磨失效。由式(69)可知,无量纲周期峰X/Arz与轴向激励频率ω、浮动环质量m、弹簧刚度ks、辅助密封阻尼cs、气膜刚度kzz以及气膜阻尼czz6个因素相关。式(69)分别对以上6个变量求偏导并令其为零,可得到周期峰X关于各变量的极大值和极小值。 根据式(69)获得的周期峰X随各影响因素的变化曲线,如图10所示。颜色加深区域为干气密封涉及的参数变化范围。由式(69)可知,周期峰关于激励频率的函数X=f(ω)为一偶函数,图10(a)所示的“X-ω”图线关于ω轴对称,这说明轴向激励的相位对周期峰没有影响。ω=0为函数X=f(ω)的极大值点,而在ω>0的小范围区间内还存在一极小值点,即低频时X随ω呈先减小后增大的变化规律,这与陈源等所得的结论一致。激励频率ω趋近于无穷时,周期峰X将趋近于轴向激励振幅Arz,也即干气密封在受到轴向持续高频激励时,动环振动的速度方向变化过快,浮动静环不能及时跟随动环运动,将处于准静止状态。 (a) 轴向激励频率 (b) 浮动环质量 (c) 弹簧刚度 (d) 辅助密封阻尼 (e) 轴向气膜刚度 (f) 轴向气膜阻尼图10 各因素对干气密封强迫振动周期峰的影响Fig.10 Influence of various factors on the forced vibration period peak of DGS 对于浮动环质量m,函数X=f(m)在m>0的区间内同时存在极小值与极大值点,随着m的增大,周期峰X呈现出先减后增再逐渐减小并最终趋近于Arz的规律,即在质量无限大时静环将由于惯性几乎不跟随动环的激励,此时周期峰等于动环轴向激励的振幅。不过实际干气密封中的石墨静环质量一般为0.1~20.0 kg,处于曲线极小值点的左侧或附近,周期峰X随m的增大呈现出单调递减或先减后增的变化规律,该极小值点是浮动环质量m的最优值,如式(70)所示。为获得较好的轴向动态追随性,建议选取密度较大的浮动环材料,不过当质量超过式(70)所示的优选值后,继续增大质量则会使干气密封的轴向动态追随性迅速恶化。 (70) 对于弹簧刚度ks和辅助密封阻尼cs,在其横轴正半轴范围内,周期峰X随着ks和cs的增大都先略有减小,后迅速增大直至趋于激励振幅Arz。考虑到实际干气密封的参数范围[24-25]一般为ks=103~107N/m,cs=101~105N·s/m,周期峰X随弹簧刚度ks和辅助密封阻尼cs的增大都呈先略有减小后迅速增大的变化规律,其中极小值点如式(71)和式(72)所示,也即当所选取的ks和cs小于极小值点时,ks和cs对周期峰影响不大,而当其超过极小值点时,周期峰迅速增大。为了获得较好的干气密封动态追随性,建议弹簧刚度和辅助密封阻尼都应不超过式(71)和式(72)所示的优选值。 (71) (72) 对于轴向气膜刚度kzz和气膜阻尼czz,其周期峰曲线的变化规律相似且与前述4个变量有着明显差别,当气膜动态特征参数趋于无穷时,周期峰X都将趋近于零而非轴向激励振幅Arz,这是因为当刚度和阻尼无穷大时,气膜类似为一刚性体,此时膜厚将基本不变。周期峰关于kzz和czz的曲线都存在一对称轴,且在对称轴处取得极大值,其中“X-czz”曲线关于czz=-cs对称,而“X-kzz”曲线则关于kzz=-(ks-mω2)对称。对于轴向气膜阻尼,由于辅助密封阻尼cs为正值,其对称轴恒在czz轴负半轴,故在干气密封实际设计中,周期峰随轴向气膜阻尼的增大单调递减,较大的轴向气膜阻尼有利于提高密封追随性。对于轴向气膜刚度,其对称轴相对原点的位置取决于弹簧刚度ks、浮动环质量m和激励频率ω的大小。轴向气膜刚度的设计应尽量远离对称轴数值,特别是当ks 密封气膜类似于一“刚度-阻尼”结构,其气膜刚度与弹簧刚度、气膜阻尼与辅助密封阻尼之间存在着最佳匹配的问题。干气密封强迫振动中刚度参数或阻尼参数对周期峰的共同影响,如图11所示。从刚度参数或阻尼参数的匹配来看,气膜刚度与弹簧刚度、气膜阻尼与辅助密封阻尼之间不存在明显的交互影响;当气膜刚度或气膜阻尼一定时,周期峰随着弹簧刚度或辅助密封阻尼的增大都呈现出先略减小后迅速增大的变化规律;当弹簧刚度或辅助密封阻尼一定时,由于在计算参数下-(ks-mω2)<0,周期峰随着气膜刚度或气膜阻尼的增大都单调递减。对于刚度而言,当弹簧刚度小于式(71)所给出的优选值,轴向气膜刚度越大时,能获得较小的周期峰;对于阻尼而言,提高轴向气膜阻尼并采用减摩手段尽可能减小辅助密封阻尼可有效提高静环挠性安装干气密封的动态追随性。总体上,在本文计算参数条件下,系统刚度参数对周期峰的影响明显大于阻尼参数的影响。 (a) 刚度影响 (b) 阻尼影响图11 刚度或阻尼参数对干气密封强迫振动周期峰的共同影响Fig.11 Joint influence of stiffness or damping parameters on the forced vibration period peak of DGS (1) 系统轴向总阻尼对干气密封轴向自由振动稳定性起决定作用;对于过阻尼系统,适当减小系统轴向总阻尼,增加系统轴向总刚度和浮环质量,使其过渡到临界阻尼或是欠阻尼状态有利于提升系统响应速度。 (2) 提出了响应最大振幅和调节时间两个参数以表征欠阻尼状态下干气密封自由振动过渡阶段的性能,获得了响应最大振幅和调节时间的解析表达式,存在最佳的系统总刚度和浮动环质量使密封兼具最短的调节时间和较小的最大振幅。 (3) 推导获得了干气密封轴向强迫振动稳定运行阶段周期峰的解析表达式,无量纲周期峰与轴向激励频率、浮动环质量、弹簧刚度、辅助密封阻尼、气膜刚度和气膜阻尼等6个因素紧密相关。 (4) 在干气密封涉及的参数范围内,当弹簧刚度和辅助密封阻尼低于某一阈值时,其数值变化对周期峰无明显影响,一旦超过某一阈值,密封轴向动态追随性迅速恶化;较大的轴向气膜阻尼有利于提高密封追随性,而只有当轴向气膜刚度大于(mω2-ks)时,增大轴向气膜刚度才有利于密封追随性。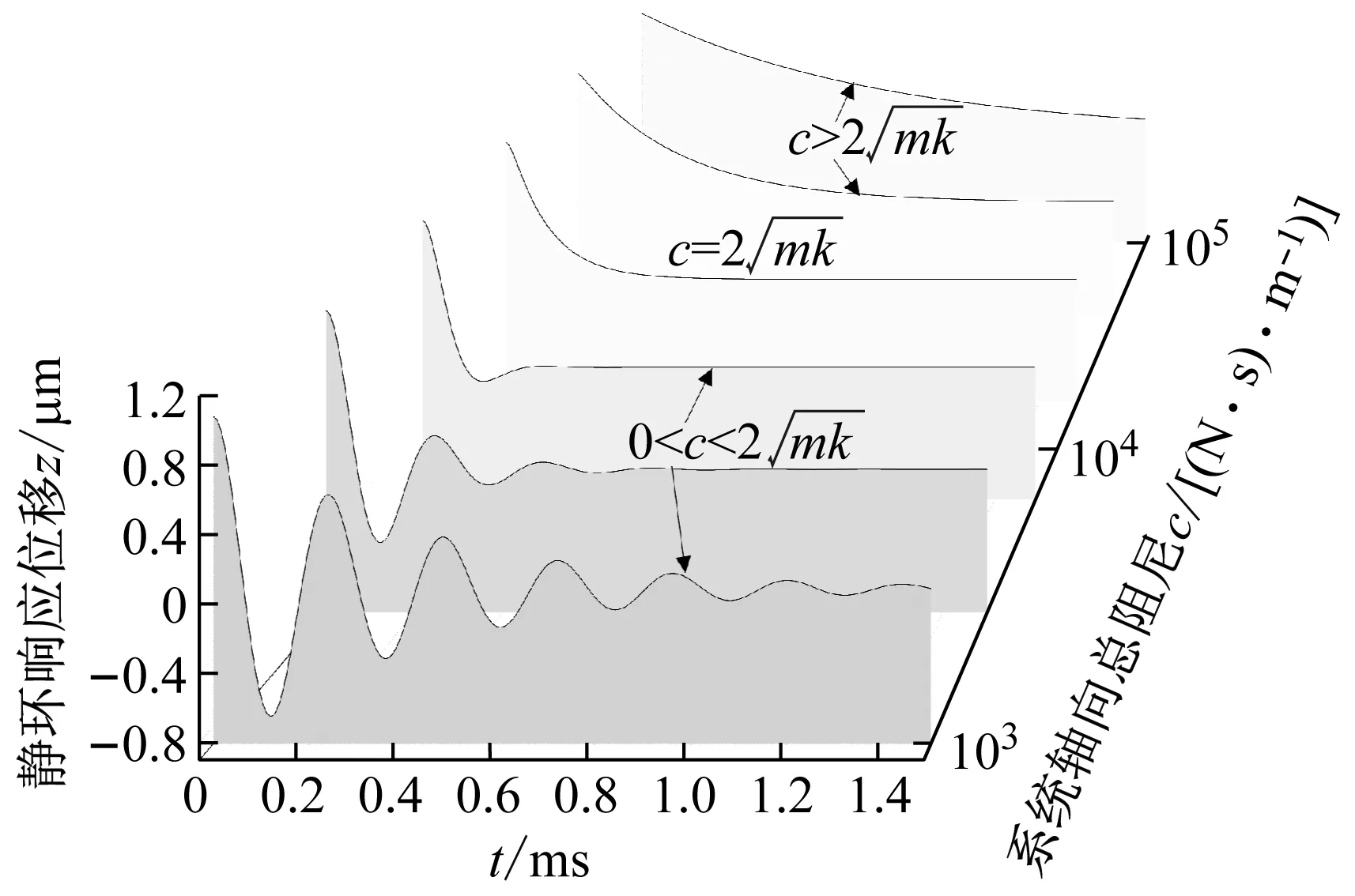
2.2 干气密封欠阻尼系统过渡阶段自振稳定性
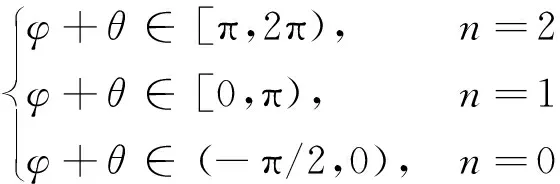
2.3 干气密封轴向强迫振动特性
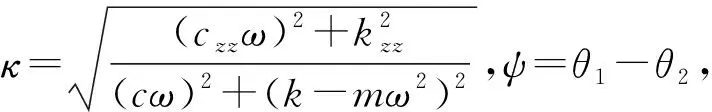
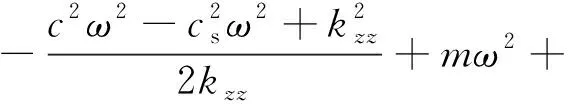
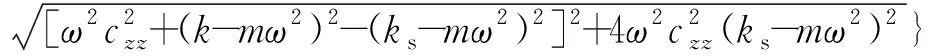
3 结 论
