丁雅杰，王佐才,2,3，辛 宇,3，戈 壁，袁子青

(1. 合肥工业大学土木与水利工程学院，安徽，合肥 230009；2. 土木工程防灾减灾安徽省工程技术研究中心，安徽，合肥 230009；3. 安徽省基础设施安全检测与监测工程实验室，安徽，合肥 230009)

结构在遭受强风、地震、海啸等极端荷载作用时会呈现出明显的非线性特性以及复杂的非线性动力学行为，非线性广泛存在于实际工程结构中，传统的基于线性模型及响应平稳性假设理论的模型修正方法难以实现非线性结构的模型修正，因此，研究非线性结构模型修正就是要对极端荷载作用下的结构劣化行为及安全性能进行有效评估。

在结构的非线性模型修正过程中，不可避免地受测试噪声、环境扰动和单元离散化等不确定性误差的影响，利用实测响应数据对非线性模型参数的不确定性进行量化，是提高非线性模型可靠性的重要手段。基于贝叶斯推理的模型修正方法结合了结构的先验信息，并利用后验概率分布量化修正后的模型参数的不确定性，因此，在有限元模型修正领域得到了广泛应用。例如，BECK 和AU[1]首次利用贝叶斯推理方法对线性结构的有限元模型进行修正，并利用Metropolis-Hastings (MH)算法实现了对剪切框架模型层间刚度的不确定性量化；易伟建等[2]考虑到多维参数的后验积分求解困难，提出利用Markov Chain Monte Carlo (MCMC)方法实现了对钢筋混凝土框架结构的损伤分析；刘纲等[3]和张建新[4]基于广义无偏先验分布，将相关向量机与MCMC 方法相结合，提高了后验样本的计算效率，实现了有限元模型修正的快速计算；WAN 和REN[5]基于贝叶斯框架，利用高斯过程模型实现对一座人行天桥的有限元模型修正，并量化由于测量噪声所引起的模型参数的不确定性；XIN 等[6]利用结构动力响应主分量的瞬时特征参数构建目标函数，并利用Cramér-Rao 边界理论实现对非线性模型参数的不确定性量化。

针对非线性结构模型修正问题，很大程度上取决于非线性特征指标的选取[7−8]。传统的非线性指标包括振动响应时程、动力响应峰值的包络以及时变模态等，难以全面地反映非线性结构的时变物理特性，因此，构造合适的非线性特征指标是进行非线性模型修正的首要任务。此外，有限元模型修正的最终目的是要定量地评价结构的可靠性，即在概率意义上定量地评价结构的安全程度。利用工程结构在服役期间的实测响应对结构的模型参数进行修正，并对其动力可靠度进行重新评估，能够较为真实地反映结构的实际安全状态[9]。根据随机振动的首次超越破坏准则，进行复合随机振动系统动力可靠度分析，是实现结构安全性评估的主要方法之一[10−12]。然而，基于跨越分析的动力可靠度理论需要同时对结构响应的联合概率密度函数和跨越过程进行假定(如Poisson假设或Markov 假设)，导致结构动力可靠度计算结果与真实值产生一定偏差。

考虑到结构振动响应主分量的瞬时加速度幅值反映了结构响应信号的幅值信息，瞬时频率则隐含了振动响应的相位信息，因此，为了实现结构的非线性模型修正及其动力可靠度计算，本文基于贝叶斯推理方法，利用实测结构动力响应主分量的瞬时特征参数作为非线性指标构建似然函数，结合拒绝延缓自适应(Delayed Rejection and Adaptive Metropolis, DRAM)算法和高斯过程模型用于非线性模型参数后验概率密度函数的快速计算。同时，利用结构动力响应的概率密度演化方法[13−14]，根据首超破坏准则对概率密度演化方程施加边界约束条件，采用Newmark-Beta 数值积分法和总变差递减(Total Variation Diminishing, TVD)差分格式进行非线性随机结构的动力可靠度计算。最后，通过数值模拟对比随机荷载作用下确定性模型和非线性随机模型的动力可靠度计算结果，并应用蒙特卡洛随机抽样验证该方法的准确性。

1 非线性结构模型修正及其动力可靠度分析理论

1.1 基于贝叶斯理论的非线性结构模型修正

随机有限元模型修正实质上是一个逆向不确定性量化过程，根据实测结构输出响应的不确定性逆推参数的不确定性，此过程用贝叶斯公式可表示为[15]：

式中：a和b分 别为参数 θ的下、上界限值。假设Y∗(θ)为由瞬时加速度幅值和瞬时频率组成的实测结构动力响应，Y(θ)为有限元模型计算的理论值，基于贝叶斯方法可建立如下模型修正表达式：

式中： θ为待修正模型参数组成的向量，θ=(θ1,θ2,···,θm)T∈Rm，m为 参数个数； ε为考虑模型误差、测量噪声等不确定性因素产生的误差向量，通常可假定为服从零均值的高斯分布，记为ε ∼N(0, Σε) ， Σε为协方差矩阵。对于进行s次独立重复试验的实测结构动力响应样本，其似然函数可表示为：

1.1.1 DRAM 算法

基于贝叶斯理论的后验概率密度函数形式复杂且与实测响应数据有关，对于具有高维参数空间的非线性结构模型修正问题，其解析解难以直接利用积分方法获得，因而，通常采用MCMC 抽样方法来近似估计待修正参数的后验分布[17]。对于传统的MCMC 方法，如MH 算法，当建议分布函数产生的候选样本参数 θ∗被拒绝后，则后验样本将保持不变，采样出现“停滞”。此外，后验样本的收敛性与建议分布的协方差函数有关，对于偏离模型参数真实分布的建议分布函数，会导致后验样本燃烧期过长、不易收敛，降低了采样效率。为了提高后验样本的接受率、加速Markov链的收敛，HAARIO 等[18]在AM 算法的基础上结合DR 策略，提出了具有自适应策略的DRAM 算法，主要包括以下两方面内容：

1)设置多重建议分布函数。根据当前参数θt利用建议分布函数q1(θt,θ∗) 生 成候选样本 θ∗，并计算样本接受率：

2)自适应更新建议分布的协方差函数。根据已生成的后验样本改变建议分布的协方差矩阵Ct，通过不断更新建议分布函数来逼近参数的真实概率分布，从而提高采样效率、缩短燃烧期，此过程可表示为：

式中：C0为建议分布初始协方差；n0为非自适应长度；sm为仅与待修正参数维度m有关的比例因子； cov(θ0,θ1,···,θt−1)为前(t−1)个已生成的后验样本协方差矩阵； ε 为 常数；Im为m维单位矩阵。DRAM 算法流程如图1 所示，其中建议分布函数个数设为q=2。

图1 DRAM 算法流程图Fig. 1 Flow chart of DRAM algorithm

1.1.2 高斯过程模型

DRAM 算法通过全局自适应策略提高了后验样本的遍历性，但仍存在计算量大的缺点，每组待修正参数后验样本的迭代均需调用有限元模型进行结构动力分析，因而计算效率十分低下。为了实现后验概率密度函数的快速计算，本文采用高斯过程模型替代有限元模型进行结构响应计算，从而大幅提高后验样本的计算效率。

高斯过程模型是基于贝叶斯框架理论发展起来的一种非参数模型，具有计算速度快、拟合精度高以及能够定量预测不确定性等特点[19]。高斯过程模型完全由均值函数和协方差函数所确定，记为：

式中：m(x) 为高斯过程均值函数；k(x,x′)为协方差函数。本文采用零均值的高斯过程模型，协方差函数包含自相关项、线性回归项、常数项以及噪声项，即：

由式(13)可知，基于训练样本可得到测试点x∗处的预测值f∗的均值mˆ∗及其方差kˆ∗。因此，对于DRAM 算法生成的候选样本 θ∗，根据式(14)可计算得到相应的动力响应预测值Y(θ∗)，利用高斯过程模型预测非线性结构动力响应，避免了耗时的非线性有限元模型时程分析，因而，能够大大提高非线性结构模型修正效率。

1.2 基于概率密度演化的复合随机结构动力可靠度分析

有限元模型修正的最终目的是要定量地评价结构的可靠性，即在概率意义上定量地评价结构的安全程度。利用实测动力响应数据对结构有限元模型进行修正，并对其动力可靠度进行重新评估，能够较为真实地反映结构的实际安全状态。

对于考虑激励和结构参数随机性的非线性随机动力系统，其随机变量记为 Θ=(θ1,θ2,···,θs)，其中s为随机变量个数，则多自由度结构运动方程可记为：

式中：X¨(t)、X˙(t)、X(t)分别为结构响应加速度、速度和位移向量；M为质量矩阵；f为包含非线性阻尼力和恢复力的结构内力向量；F(Θ,t)为随机激励向量。对于一般的结构振动系统，式(15)有依赖于随机变量 Θ的唯一解，设系统的状态量Z(t)记为：

式中：pZΘ(z,θ,t) 为 向量 [Z(t),Θ]的联合概率密度函数； Ωt、 ΩΘ分别为振动系统的时间域和 Θ的参数空间。进一步求偏导可得广义概率密度演化方程[20 − 21]：

式中，Z˙(θ,t)=∂H(θ,t)/∂t为Z(t) 在 { Θ=θ}条件下的速度；式(18)的初始条件为：

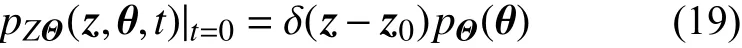
对于式(18)和式(19)构成的偏微分方程，可利用TVD 格式的差分方法进行求解[22]，通过积分得到随时间变化的结构动力响应演化概率密度函数pZΘ(z,θ,t)。

基于首超破坏准则的结构动力可靠度可记为[23]：

式中， Ωs为安全域。当发生事件 {Xlim(τ)∈Ωf}时，则结构失效， Ωf为失效域。首超破坏准则条件下一旦结构响应超出安全域边界 ∂Ωs进入失效域 Ωf，则该事件的概率不再返回安全域，其留在安全域内的总概率即为结构的动力可靠度。因此，对式(18)施加位移边界约束条件：

结合边界条件式(21)、初始条件式(19)可求解广义概率密度演化方程式(18)，进而得到结构的动力可靠度：

2 非线性结构模型修正

2.1 模型概况

本文以具有非线性Bouc-Wen 模型的层间剪切型框架结构为例，根据贝叶斯推理方法实现结构非线性模型修正及其参数不确定性量化。如图2所示，该结构为五层剪切框架，层高3m，结构质量自顶层至底层依次为7.1×104kg、3.1×105kg、4.8×105kg、5.1×105kg、5.3×105kg。柱截面尺寸为500 mm×500 mm，初始弹性模量E=3.2×104MPa，其单元恢复力曲线为图3 所示的Bouc-Wen 模型，数学表达式为：

图2 五层非线性剪切模型 /mFig. 2 Five-layer nonlinear shear model

图3 Bouc-Wen 模型Fig. 3 Bouc-Wen model

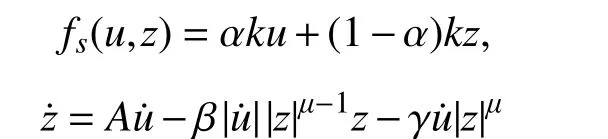
式中：k为结构的弹性刚度；z为滞变位移；u为相对位移； α为水平刚度屈服比；A、 β 、 γ、μ为Bouc-Wen 模型滞回环控制参数，非线性Bouc-Wen模型参数的初始设计名义值如表1 所示。

表1 非线性Bouc-Wen 模型参数的名义值Table 1 Nominal value of nonlinear Bouc-Wen model parameters

2.2 高斯过程替代模型建立

取非线性Bouc-Wen 模型参数作为待修正参数，其名义值如表1 所示。利用Opensees 有限元软件计算该剪切框架在峰值加速度PGA=0.20g的Northridge 地震动作用下的结构动力响应，其顶层加速度时程曲线如图4 所示。利用离散解析模式 分 解(Discrete Analytical Mode Decomposition,DAMD)方法[24]和Hilbert 变换对顶层加速度响应进行信号分解，并提取结构振动响应主分量的瞬时加速度幅值和瞬时频率慢变成分。由于主分量的瞬时特征参数相比于加速度响应随时间变化较为缓慢，因此，分别选取瞬时加速度幅值和瞬时频率慢变成分的30 个局部峰值点作为非线性指标来构建似然函数，如图5 所示。为了提高非线性结构模型修正计算效率，首先利用高斯过程模型建立非线性模型参数与结构瞬时特征参数的回归关系，定义非线性模型参数在名义值的80%范围内波动，故待修正参数[ α ,A,μ, β , γ]的上下界限值分别为[0.72, 1.8, 5.4, 0.9, 0.9]和[0.08, 0.2, 0.6,0.1, 0.1]。本算例中，根据Sobol 序列采样法抽取200 组Bouc-Wen 模型参数训练样本，并利用Opensees 有限元模型计算其对应的结构主分量瞬时特征参数。采用留一法交叉验证高斯过程模型的拟合精度，以第10 s 处结构瞬时加速度幅值为例，其相应的交叉验证残差的正态分位图如图6所示。由图6 可知，留一法交叉验证残差的正态分位图趋于直线，表明残差的正态特性好，因而可判断建立的高斯过程模型能够很好地预测结构的瞬时特征参数。

图4 结构顶层的加速度响应Fig. 4 Acceleration response of top floor

图5 结构主分量瞬时特征参数Fig. 5 Instantaneous characteristics of principal component response

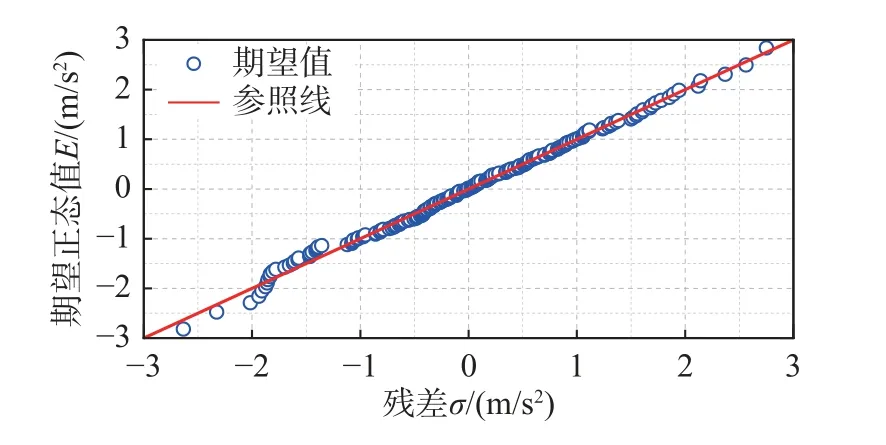
图6 残差正态分位图Fig. 6 Normal quantile-quantile plot

2.3 考虑不确定性的结构非线性模型修正

2.3.1 考虑测量不确定性的非线性模型修正

为了考虑测量不确定性的影响，对非线性模型参数名义值下的顶层加速度响应，施加30 组噪信比为5%的高斯白噪声，得到30 组响应数据，并以此作为实际结构的测量值。分别采用DRAM算法和MH 算法进行贝叶斯模型修正，设置迭代终止次数T=8000，非自适应长度n0=200，建议分布函数个数q=2。同时结合已建立的高斯过程模型来提高非线性模型参数后验概率分布的计算效率。随机选取待修正参数的初始值为[ α ,A,μ, β , γ]ini=[0.2, 0.4, 2.5, 0.8, 0.7]，分别利用DRAM 和MH 算法计算得到参数 γ的Markov 链如图7(a)和图7(b)所示，非线性Bouc-Wen 模型修正结果列出如表2，从图7 和表2 可以看出，DRAM 算法通过自适应调节建议分布函数，提高了后验样本的遍历性，与MH 算法计算结果相比，DRAM 计算得到的后验样本均值与名义值误差较小，样本接受率高，且待修正参数后验样本变异系数均小于0.04，因此，利用DRAM 进行参数后验概率估计可以较为快速、准确地量化模型参数的不确定性。同时，基于高斯过程模型和DRAM 算法的非线性模型修正过程运行时间为42 s，与传统基于有限元模型计算的蒙特卡洛抽样法相比计算效率得到了大幅提高。

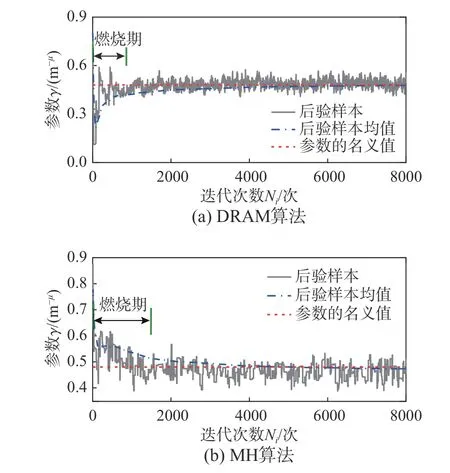
图7 参数γ 的马尔科夫链Fig. 7 Markov chain of γ

表2 非线性Bouc-Wen 模型参数修正结果Table 2 Updated results of nonlinear Bouc-Wen model parameters

2.3.2 考虑结构参数不确定性的非线性模型修正

取非线性Bouc-Wen 模型参数为待修正参数，为了考虑结构参数的不确定性，设其为符合正态分布的随机变量，均值为表1 所示参数初始设计名义值，标准差均为0.1。根据结构非线性模型参数的概率分布随机生成30 组样本，并代入有限元模型计算得到30 组结构顶层加速度响应，根据DAMD 方法和Hilbert 变换提取每组结构响应主分量的瞬时特征参数作为“测试值”。以第10 s 处主分量响应的瞬时加速度幅值为例，计算得到30 次测试值如图8 所示，利用表1 所示参数名义值计算得到的瞬时加速度期望值为1.19 m/s2，从图8 可以看出模拟得到的瞬时加速度幅值响应在期望值附近波动，满足贝叶斯推断中误差的高斯分布假设。

图8 模拟的30 次瞬时加速度幅值Fig. 8 30 sets of simulated instantaneous acceleration amplitudes

结合高斯过程替代模型，利用DRAM 算法进行贝叶斯模型修正，设置迭代终止次数T=8000，非自适应长度n0=200，建议分布函数个数q=2，待修正参数初始值设为 [ α ,A,μ, β , γ]ini= [0.2, 0.4,2.5, 0.8, 0.7]。以参数 γ为例，其Markov 链和剔除燃烧期后的样本直方分布分别如图9(a)和图9(b)所示。非线性结构模型修正结果如表3 所示。从图9和表3 可知，待修正参数的Markov 链燃烧期较短，样本接受率相比于考虑测量不确定性的计算结果较高，原因归结于生成测量样本的非线性模型参数严格服从正态分布，DRAM 算法通过自适应策略快速调整建议分布协方差函数逼近待修正参数的真实分布，加速了后验样本的收敛。表3中后验样本均值与名义值的误差较小，因此，采用本文提出的基于贝叶斯理论的非线性模型修正方法可以应用于考虑多种不确定性误差的非线性结构模型修正问题。

表3 非线性结构模型修正结果Table 3 Updated results of nonlinear model

图9 参数γ 的后验样本Fig. 9 Posterior samples of γ

3 结构动力可靠度分析

3.1 非线性动力响应概率密度演化分析

利用实测结构动力响应对结构模型参数进行识别，并对其动力可靠度进行计算，是结构安全性评估的重要手段。以第2 节中地震动作用下具有随机非线性参数的剪切框架为例，进行结构动力可靠度分析，其中非线性模型参数采用2.3.1 节中表2 所示的DRAM 算法修正结果。结构受Northridge 波形地震动作用，分别以地震动峰值加速度(PGA)和非线性Bouc-Wen 模型参数为随机变量，其概率分布统计如表4 所示。

表4 非线性模型随机参数与激励随机参数Table 4 Random parameters of nonlinear model and excitation

记框架结构顶层位移为x(t)，同时考虑非线性结构模型参数与激励参数的随机性，根据概率密度演化方法计算得到x(t)在不同时刻的概率密度曲线及累积分布函数，如图10 所示。图11 给出了不同时段内结构动力响应的概率密度函数曲面及其对应的等值线图，从图10 和图11 可以看出，结构响应的概率密度函数随着时间不断变化且趋于复杂，概率密度曲线具有明显的演化特征不再服从规则的概率分布函数，因此，在传统结构动力可靠度分析中将结构响应假设为以正态或极值分布为代表的规则分布，可能会导致结构可靠度计算结果出现偏差。

图10 不同时刻概率分布Fig. 10 Probability distribution of different time

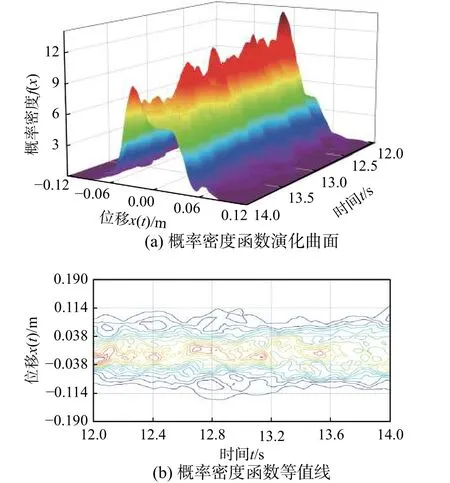
图11 不同时刻概率密度演化Fig. 11 Probability density evolution of different time

此外，根据概率密度演化方法计算得到的结构顶层位移均值和标准差及其与蒙特卡洛随机抽样的比较见图12。在蒙特卡洛模拟中，首先根据随机参数的概率分布抽取10 000 组样本，然后利用抽取的样本参数进行确定性结构响应计算，并统计结构位移响应的均值和标准差。图12 对比结果表明，基于概率守恒原理的广义概率密度演化方法与随机蒙特卡洛模拟结果相比误差较小，因而能够较为真实、准确地反映实际结构动力响应概率分布的演化过程。

图12 结构顶层位移时程均值和标准差对比Fig. 12 Comparison of time history mean and standard deviation of top floor displacement

3.2 结构动力可靠度计算

为了考虑参数不确定性对结构动力可靠度的影响，分别建立了两种非线性振动模型：1)仅考虑激励随机性的确定性非线性模型，结构模型参数为表1 所示的名义值，记为名义模型；2)同时考虑激励和结构模型参数的不确定性，按照表4随机参数概率分布建立的复合随机模型。

根据首次超越破坏准则，利用广义概率密度演化方法，分别对不同界限条件下的结构动力可 靠 度R(t) 进 行计算，其 中R(t)=P{|x(τ)|≤xlim,τ∈[0,t]}，t=30 s。为了验证计算结果的准确性，利用蒙特卡洛模拟方法对复合随机模型的动力可靠度进行随机抽样计算。

分别利用顶层位移和速度作为边界条件指标，计算非线性结构的动力可靠度。不同位移界限条件下结构动力可靠度计算结果如图13 和表5所示；不同速度界限条件下的计算结果见图14 和表6。由表5 和表6 可知，基于概率密度演化的结构动力可靠度计算结果与蒙特卡洛抽样模拟相比误差较小，具有较高的计算精度，且名义模型在不同类型界限条件下的动力可靠度均大于复合随机模型，非线性模型参数的不确定性降低了结构的动力可靠度。此外，当名义模型分别在位移和速度界限条件下动力可靠度达到1.000 时，复合随机模型的动力可靠度分别为0.9808 和0.9475，由此可知，以速度作为界限条件相比于位移使得复合随机模型的可靠度计算结果偏低，不同类型界限指标对结构动力可靠度的计算结果会产生一定的影响，因此，在结构安全评估中应充分考虑非线性模型参数的不确定性，使得结构动力可靠度计算结果更加合理、准确。

图13 不同位移界限条件下结构动力可靠度Fig. 13 Dynamic reliability under different displacement boundary conditions

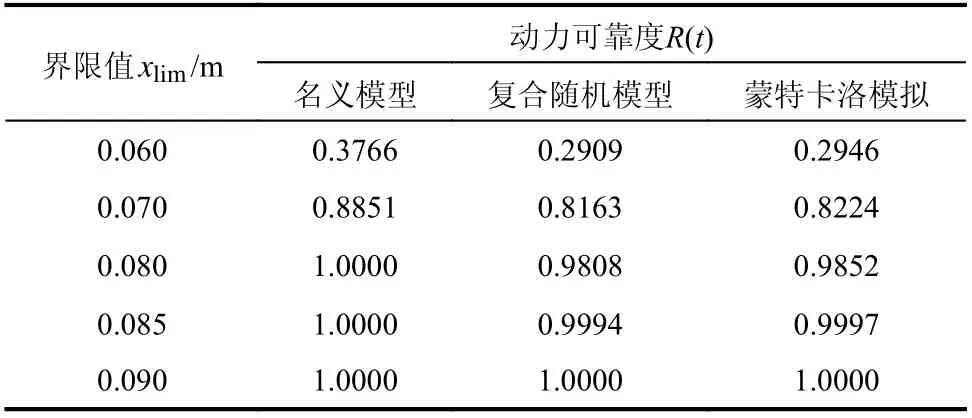
表5 不同位移界限条件下结构动力可靠度对比Table 5 Dynamic reliability for different displacement boundary conditions

图14 不同速度界限条件下结构动力可靠度Fig. 14 Dynamic reliability under different velocity boundary conditions

表6 不同速度界限条件下结构动力可靠度对比Table 6 Comparison of dynamic reliability for different velocity boundary conditions

4 结论

本文基于实测结构动力响应主分量的瞬时特征参数构建贝叶斯推理的似然函数，并结合DRAM 算法和高斯过程替代模型，实现了结构的非线性模型修正和参数的不确定性量化。同时，根据非线性模型修正结果，采用广义概率密度演化方法对实测结构进行安全可靠度评估。通过地震激励下非线性框架结构的数值模拟结果，得到以下结论：

(1)结构动力响应瞬时特征参数包含了振动系统的幅值和相位信息，能够较为全面地反映时变非线性结构的物理特性。利用有限个局部峰值点的瞬时特征参数建立似然函数，能够准确识别结构的非线性模型参数并对其不确定性进行量化。

(2)通过将DRAM 算法和高斯过程替代模型相结合，克服了传统MCMC 方法样本接受率低、燃烧期长等缺点，大大提高了待修正参数后验样本的计算效率，简化了非线性结构模型修正的过程。

(3)根据首次超越破坏准则，利用广义概率密度演化方法能够准确计算结构的动力可靠度。与确定性模型相比，考虑非线性模型参数不确定性的复合随机模型能够更加真实地反映结构的安全状态，其动力可靠度计算结果总体偏低，因此，在结构安全状态评估中，考虑模型参数的不确定性能够更好地反映实际结构的抗震性能水平。