吴上生，陈 柘，兰 侨

（华南理工大学机械与汽车工程学院，广州 510630）

0 引言

剪叉可展结构由于其结构紧凑、承载量大和易操作性，收缩时占用空间小，展开时可以达到并稳定设想的状态，因此在现代物流、航空装卸等领域中得到广泛应用[1]。结构能否顺利按设计要求展开和收缩，是在剪式可展结构设计中首先需要考虑的问题，因此需要对可展结构进行运动学分析，以验证是否满足要求。Travis L[2]推导了剪式折叠机构在展开过程中的运动方程；徐坤[3]对剪式弯曲折展机构建立了机构单元运动的数学模型，然后分析了该机构的自由度和运动形式；杨毅[4]利用螺旋理论对剪铰多面体机构进行了自由度和奇异性分析；吴新燕[5]从驱动机构、连杆机构、驱动方式等的优化出发，验证了环形桁架结构的顺利展开。在满足运动学要求后，需要进行可展结构的动力学分析，得到在外力作用下的运动规律。纪斌[6]对非对称平面剪铰单元进行了分析，讨论了速度、加速度等物理量的动力学特性；李博[7]在基于剪式线性阵列可展结构对称性的动力学分析方法研究方面，提出了坐标和速度修正方法，得到了剪式单元各节点物理量的变化过程，但结构过于简单，该方法的针对复杂结构的普适性没有得到验证。彭麒安[8]针对剪式单元阵列可展结构提出了一种规范化动力学分析方法，大幅度地降低组装难度，提高建模效率。Sun-Yuantao[9]结合虚功原理和螺旋理论对可展结构的动力学行为和展开过程进行了分析。杨玉龙[10]采用一种基于向量式有限元法建立剪式结构力学模型，对展开过程进行模拟，比较了刚性杆和柔性杆的展开速度及时间。Yang Tao[11]提出了一种非交叉结构元件的剪式可展机构，构造了具有径向膨胀运动的可展开多面体机构，获得了较大的变形能力，同时仿真验证了其展开过程，但过多关注于结构机理，缺乏动力学理论分析。

本文研究的剪式可展结构是连杆式可展结构的一种，与大多数可展结构杆长都相等不同，本文所用连杆有短杆和长杆两种，短杆和长杆经销轴连接成剪式铰，具有运动收缩功能，短杆起传递力矩和支撑连接长杆等作用，相对于传统的两杆铰接可展结构具有更强的抗变形能力。首先，利用几何关系推倒其运动学规律，其次，根据约束条件建立基于拉格朗日乘子法的动力学方程，采用Baumgarte约束违约稳定法对系统的坐标和速度进行修正，避免数值结果的发散，最后利用MATLAB 完成展开过程数值仿真，得到其运动规律。

1 剪式可展机构的运动学分析

如图1 所示，本文所研究的剪式可展机构由连杆和销轴组成，各杆之间铰接，各杆的端点分别用数字1、2、3、4、5、6、7、8 表 示，各杆的杆长由Lij表示，其中i、j分别代表端点。取端点1 为坐标原点建立直角坐标系xoy，端点1 和端点8 是固定不动的，两端点之间的距离为L，连杆16 和连杆28 可以分别绕端点1和端点8 转动，结构的动力系统假设为固定在点6 上并只能提供沿x轴负方向的恒力，显然连杆16 转动角速度是时间t的函数。

剪式可展单元是单自由度系统，因此其运动规律可以用某一时刻连杆16 的转角θ来描述。假设某t时刻单元的位形如图1所示，其中杆16与x轴的夹角为θ，杆28与x轴的夹角为φ，端点1、端点8 的坐标显然分别为（0，0），（0，L），下面推导其余6个端点的坐标。

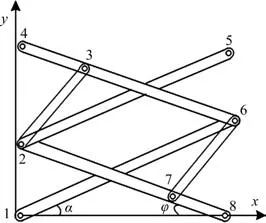
图1 剪式可展单元结构简图

根据杆长和角度关系可得端点2、端点6、端点7 的坐标分别如下。

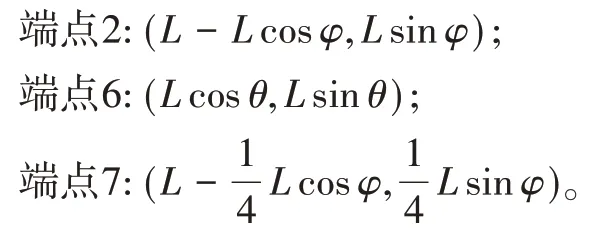
根据端点2、3、6、7 所组成的平行四边形关系，角度在第二级可展单元得到继承，角度如图1 所示，由此可以得到端点3、端点4、端点5的坐标分别如下。

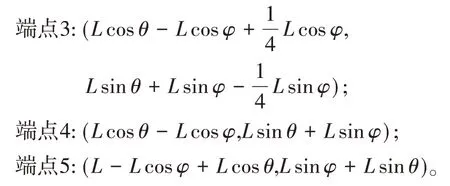
为了建立φ和θ的关系，使得坐标方程中只有一个变量，可利用端点6和端点7的杆长限制坐标关系，得到以下关系式：

由三角函数关系式：

联立公式（1）、公式（2）可以得到两个角度关系如下：

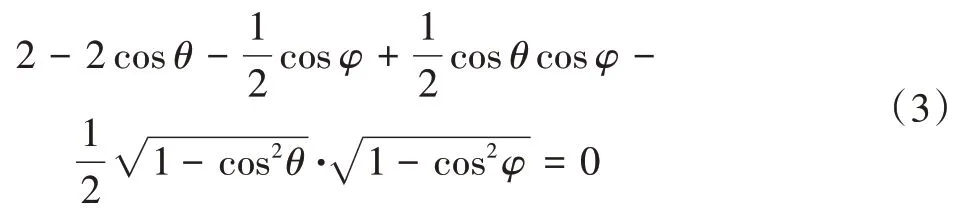
通过上述分析得到了剪式可展单元的整体坐标矩阵，每个坐标均是杆16 与x轴夹角θ的函数，由此可以确定结构在每一时刻的状态，且相互连接的剪式单元的运动不是相互独立的，一个杆件的运动势必会影响与其相连的杆件。

2 剪式可展单元的动力学分析

2.1 等效质量矩阵

假设剪式可展结构由n个等截面直刚杆组成，将每个杆件都得端点作为节点，则有2n个节点，6n个笛卡尔坐标，结构系统的位姿即剪式可展结构空间位置的坐标集合可由这6n个笛卡尔坐标来描述。取杆ij作为分析对象，则两端点的坐标可以表示为：

该杆件上任一点的速度矢量可表示为：

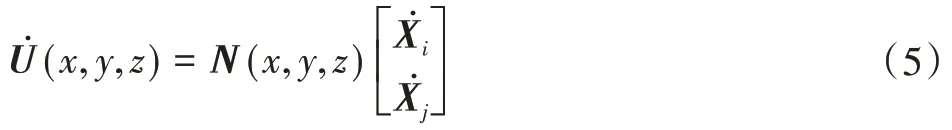
N(x,y,z)为杆单元速度函数矩阵，其具体形式如下：

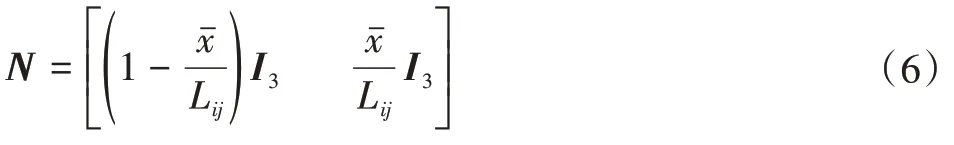
式中：Lij为杆ij的杆长；xˉ为任一点X到端点i的长度；I3为三维单位矩阵。

单元动能可以表示为：

当杆件截面面积A相同，密度ρ相同时，式（7）可写为：

式中：M(e)为单元的等效质量矩阵；V(e)为杆单元体积。

由式（8）可得杆单元的等效质量矩阵：

本文研究对象剪式可展单元的展开收缩可以看作是在平面内完成，则对于平面杆单元，其等效质量矩阵可以简化为：

将各单元刚度矩阵按照节点号进行下标转换，将转换后的单元刚度矩阵投放到总体刚度矩阵的对应位置上，按照叠加法可以获得结构的整体质量矩阵。

2.2 约束方程

在剪式可展结构中，存在3 种约束，即杆长约束、铰接点约束、端点边界约束。杆长约束表示在结构运动过程中各个端点坐标发生改变时，同一个杆件的两端点之间的距离不变；铰接点约束表示使得两个杆件形成铰接的端点在运动过程中相对于这两个杆件的相对位置坐标不变；端点边界约束表示剪式结构中端点固定不变的坐标关系，包括端点的固有坐标以及两端点的限制关系坐标。

杆长约束如下所示：

图1 所示剪式线性阵列结构有6 个杆单元，则对应的杆长约束方程共有6 个，分别将杆件各端点坐标及杆长代入上式得到。

铰接点约束如下所示：

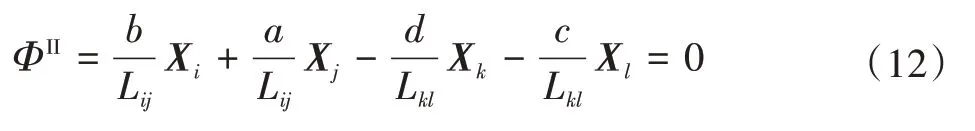
式中：Xi、Xj、Xk、Xl分别是铰接处不同杆件的端点坐标；a、b、c、d分别是指各端点到销轴处的距离。

图1 的剪式可展结构有4 个铰接点，故相应的铰接点约束方程有4个。

图1 中的端点1、端点8 采用与地面的铰接，故这两点的坐标均为定值；为了保证剪式可展机构伸展收缩时端点4、端点5在同一高度，因此需要限定这两端点的距离保持不变。以上两种边界约束条件用方程表达可如下式：

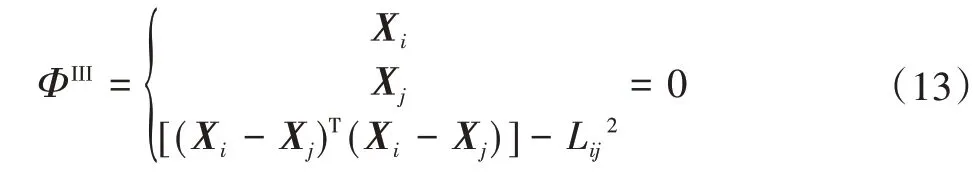
为了方便后续的计算，建立系统的广义坐标矩阵，将各个端点坐标集合表示系统的位形。由上述公式（11）～（13）约束方程可将系统的总体约束关系表示为矩阵形式如下：

对约束方程求解偏微分方程可以得到约束条件下的雅可比矩阵Φq。

2.3 基于Baumgarte违约稳定法的动力学方程

针对一般系统模型，建立动力学方程的方法常用的有虚功原理、达朗贝尔贝尔原理、拉格朗日方程等。前两种方法适用于已知系统能量描述的情况下，而拉格朗日方程适用于已知系统力的关系及坐标关系的情况下。本文使用拉格朗日乘子法[12]建立在约束方程基础上的剪式可展单元系统的动力学方程：

式中：M为质量矩阵；̈为约束系统的加速度矢量；Φq为 雅 可 比 矩 阵；λ为 拉 格 朗 日 乘 子， 取 为λ=(λ1,···,λs)T，s为约束方程的个数；F为系统所受广义外力矩阵。

求解微分方程时，需要给定合适的初始解，才能获得方程的唯一解，针对式（15）需要已知速度矢量和加速度矢量，故可对约束方程（14）求一阶导数获得速度约束方程，求二阶导数获得加速度约束方程：

联立方程（15）和方程（17）可以得到增广形式的动力学方程：

在利用上式进行数值积分计算时，由于方程只显含加速度约束条件，故所得结果仅对加速度收敛，为了保证所得结果同时对位移、速度、加速度收敛，引入Baumgarte 约束违约稳定法进行求解，在上式中加入速度和位移的修正量，将式（17）改为：

此时动力学方程改为：

式中：α、β均为大于0的修正系数，一般α、β取值范围为5～50时对结果违约校正效果较好。

3 算例分析与仿真结果

在推导出系统质量矩阵的基础上，在i时刻，首先得到约束方程Φi，并求解一节偏微分得到雅可比矩阵，进一步地通过式（17）求出加速度右项ηi，结合系统受力、坐标和速度初始条件，根据式（20）求解方程可以得出q̈i，对q̈i进行数值积分，可以得到此时刻的速度q̇i以及坐标qi，将所求得的速度和坐标分别代入式（14）、式（16），如果满足精度范围，则进行下一轮循环，直至完成预设时间内的所有数值解。

见图2，由4 个长连杆和2 个短连杆组成的剪式可展结构，L16=0.436 m，L28=0.436 m，L25=0.436 m，L46=0.436 m，L23=0.16 m，L67=0.16 m，铰点7 和铰点8 的距离为L28∕4，铰点3 和端点4 的距离为L46∕4。6 只连杆的横截 面A=0.02 m×0.03 m，密 度ρ=7 850 kg∕m3，端点1 和端点8 坐标固定，但能绕各自铰点转动，在端点6 处有一驱动器，恒定为F=20 N 沿着x轴负方向，在驱动器作用下，该剪式可展结构可以伸展或收缩。

图2 剪式可展单元组成及长度标号

取各端点坐标为系统的广义坐标如下：

根据式（10）可以得到系统组装后的质量矩阵为：

式中：

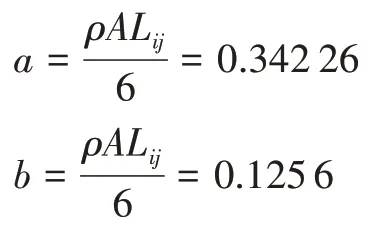
由式（11）～（13），根据系统的杆长约束、铰接点约束、端点边界约束，可得全部约束方程如下：

对上式约束方程求解偏微分可以得到约束方程的雅可比矩阵：

式中带两个下标的元素表示两个坐标的差值，如：xij=xi-xj，代表xi和xj的坐标之差。

根据式（17）求得的加速度右项为：

根据前节描述，可以知道系统所受力的广义矩阵为：

在代入已知初始时刻的位置矢量和速度矢量后，将式（21）～（25）代入式（20）中，采用Runge-Kutta 法完成数值积分运算，可以得到在展开过程中剪式可展单元各端点的位置、速度、加速度随时间的变化曲线，如图3～5所示。

图3 节点x方向位移随时间变化曲线

由图3 和图4 看出，剪式可展结构在展开过程中在x方向上的坐标变化不大，而在y方向上变化很大，这极大发挥了可展结构的特有优势，即很小范围的驱动能够实现更大范围的展开空间。从图5和图6可得到速度随着展开高度的增加越来越快，且非受力一侧的节点速度要大于受力一侧的节点速度，如节点2、节点3 不论是x方向速度还是y方向速度都比相对应的节点6 和节点7 的速度要快，这是本文所研究的含有不同杆件长度的剪式可展单元的特有属性。由图7 和图8 可知，在展开过程中，x方向上的加速度在给定时间内一直呈增加的态势，而在y方向上，各节点的加速度在增加到一个峰值后会降低，且加速度降低速度更快，时刻表1 s 中累积的幅值，仅用时0.3 s 就降低到时间地点时刻的加速度，这表明剪式可展机构展开过程较复杂，工程应用时，为了保证结构能够稳定展开，需要根据图5～8 反馈的信息制定合理的控制策略，以满足实际的需求。综合位移、速度、加速度随时间的变化关系来看，本文所设计的一种含不同杆件长度的剪式可展机构整体运行平稳。

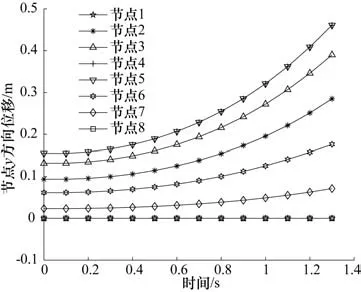
图4 节点y方向位移随时间变化曲线

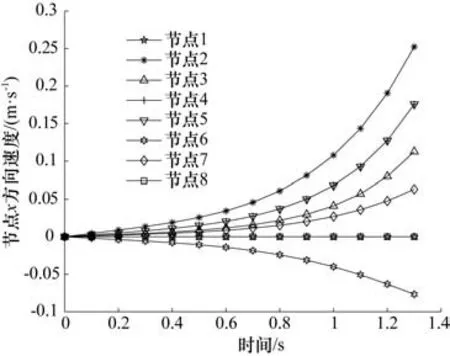
图5 节点x方向速度随时间变化曲线

图6 节点y方向速度随时间变化曲线

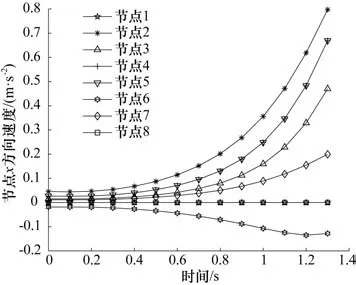
图7 节点x方向加速度随时间变化曲线

图8 节点y方向加速度随时间变化曲线

4 结束语

（1）本文提出一种由不同长度杆件组成的剪式可展单元结构，该结构在承载时不像传统剪式结构随着高度的升高重量会偏向一侧，造成受力不均影响稳定性，反而伸展过程中最底部的铰点位置不变，有效提高结构的强度和稳定性。

（2）根据剪式可展单元的基本约束关系，即杆长约束、铰接点约束、端点边界约束，建立了结构的动力学模型，采用基于Baumgarte违约稳定法使方程得到收敛的结果。

（3）剪式可展结构在展开过程中在x方向上的坐标变化不大，而在y方向上变化很大，这极大发挥了可展结构的特有优势，即很小范围的驱动能够实现更大范围的展开空间。且非驱动力一侧的节点速度要大于受驱动力一侧的节点速度，如节点2、节点3 不论是x方向速度还是y方向速度都比相对应的节点6 和节点7 的速度要快，这是本文所研究的含有不同杆件长度的剪式可展单元的特有属性。研究结果可以为对称剪式机构的工程应用和制定展开过程的精确控制提供理论依据。