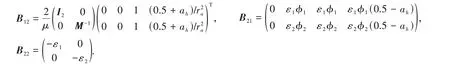黄熙文，陈衍茂，李文龙，刘广

中山大学航空航天学院，广东 广州 510006

近几十年来，已有大量关于翼型气动弹性响应预测和分析的研究［1-3］。作用在机翼上的亚音速来流，通常采用Theodorsen理论来进行气动力建模［4-5］。在该理论中，升力和俯仰力矩系数均由卷积积分建立［6］。由于系统方程同时包含微分和积分算子，因此使用数值方法直接求解是相当困难的［6］。并且从计算的角度来看，求解积分方程比解微分方程困难得多。

众所周知，通过Newmark-β法等时程积分方法［7-8］，可以方便地模拟仅包含微分算子的状态空间模型。但倘若同时存在积分项，此类振动方程则很难化简为状态空间方程。对于亚音速来流作用下的气动弹性系统，Lee 等［9］通过引入4 个辅助变量，将同时包含卷积积分的系统，化简为由8 个常微分方程表示的状态空间模型。Trickey［10］则提出了另一种建模方法，通过使用拉普拉斯变换的方式成功处理了卷积，该方法的状态空间模型仅包含6 个常微分方程。此外，Coller 和Chamara［11］也提出了一种仅用6 个常微分方程表示气动弹性系统的方法。上述三种状态空间方程在过去数十年中都得到了广泛的应用。Lee等建立的模型，被广泛应用于具有结构非线性的气动弹性系统中，包含立方、间隙以及滞回非线性等模型中［12-15］。Trickey等的模型，通常应用于带有控制面的气动弹性系统的颤振抑制问题中［16-18］。Coller等提出的模型多用于研究极限环颤振和双颤振的性质［19-20］。

上述三种气动弹性系统状态空间模型之间是否等价，对于气动弹性系统的研究至关重要。但是，目前还没有解析研究或数值分析证明它们之间是完全等价的。在本文中，我们将分别推导翼型气动弹性系统的三种状态空间模型，并从数学上证明三种化简模型是等价的，再通过数值结果进一步验证三者之间的关系。

1 翼型气动弹性系统的状态空间模型

二元机翼模型如图1 所示，其在俯仰方向和沉浮方向上振动。定义弹性轴的俯仰角度为α（抬头为正），沉浮位移为h（向下为正）。弹性轴位于距机翼中点的ahb处，质心位于距弹性轴xαb处。

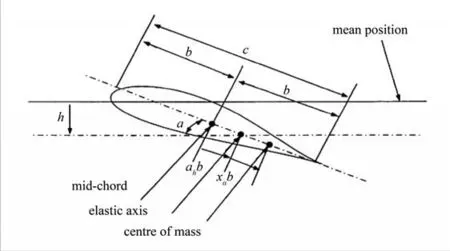
图1 俯仰和沉浮方向振动的二元机翼模型［6］Fig.1 Sketch of an airfoil oscillating in pitch(α)direction,and in plunge(h)direction[6]

考虑亚音速来流，机翼运动的耦合方程可表示为［6］

根据Theodorsen空气动力学模型［1］，在不可压非定常流作用下，升力CL(t)和力矩CM(t)系数为

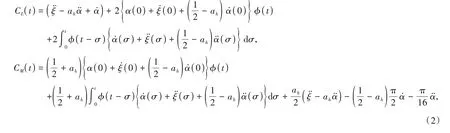
1.1 模型1（Lee等的模型）

为消除积分算子，Lee等［9］引入如下形式的4个辅助变量

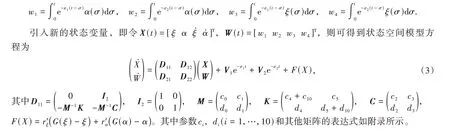
1.2 模型2（Trickey等的模型）

根据式（2），升力中的积分可展开为

1.3 模型3（Coller和Chamara的模型）

根据Coller和Chamara的研究［11］，升力中的积分可以表示为

通过简单的计算，可以推导出如下常微分方程组

从本质上讲，这种方法与Coller和Chamara提出的方法是相同的。

2 等价性证明

式（9）中的最后两个方程可表示为

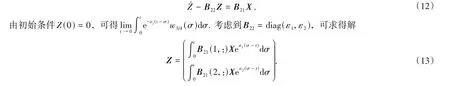
将式（13）代入到式（9）的前4个方程中可得

将以上4个方程代入式（14）中可得

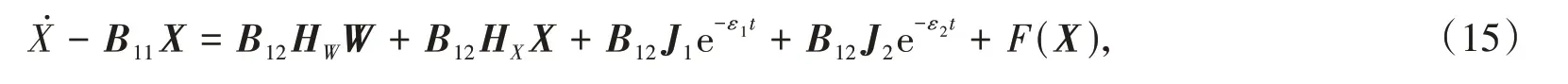
其中

另一方面，系统（3）中的前4个方程可表示为

经过计算，可以发现B11+B12HX=D11，D12=B12HW，V1=B12J1以及V2=B12J2. 此外，式（16）中的非线性项与式（15）中的完全一致。因此，可以得出结论：式（15）与式（16）完全相同，系统（9）与系统（3）是等价的。

对于系统（7），将式（7）中最后两个方程写成为

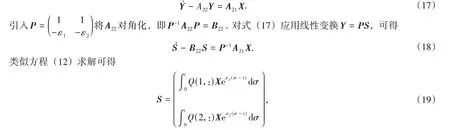
其中Q=P-1A21. 将式（19）代入Y=PS中，可将系统（7）的前4个方程写成为

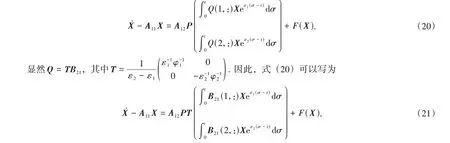
因此，式（21）与（14）是等价的，其中A12PT=B12，这说明本质上模型2与模型3是等价的。

3 数值验证

接下来，我们将对上述三种模型进行数值验证。其中系统参数设置为μ= 100，rα= 0.5，ah= -0.5，ζα=ζξ= 0，ωˉ= 0.25，xα= 0.25。根据Hopf 分岔理论，可以获得系统的分岔点为Uf= 6.038 5。当无量纲来流速度U超过Uf时，系统的平衡点X= 0将失去稳定性，即系统将产生极限环振荡［6］。

基于状态空间模型，可以通过如龙格-库塔法等数值方法，求得系统（3）、（7）、（9）在任意给定初始条件下的数值解。为了便于对比，使用下标1、2和3分别表示系统（3）、（7）和（9）的解。考虑线性系统，即G(ξ) =ξ，M(α) =α，沉浮方向的位移可表示为ξi(t)(i= 1，2，3)。当初始条件都设置为X(0) =[0.2 0.1 0 0]T时，三种模型的解完全一致，如图2 所示。在接下来的所有讨论中，初始条件都设为上述值。此外，图2 还给出了三个位移之间的残差。可以看到，RK 法获得的结果的残差数量级在10-6到10-5之间，远远小于位移解的数量级10-1。为了进一步验证三种模型之间的等价性，可采用精细积分法［23-24］（PIM）来求解原系统。可以看到，精细积分法的解对应的残差误差在10-14数量级。显然，这种级别的残差是由计算机截断误差造成的。

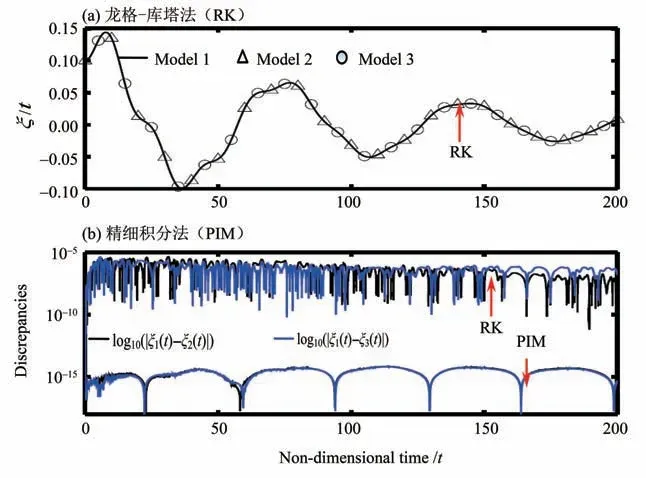
图2 龙格-库塔法（RK）和精细积分法（PIM）计算的沉浮方向位移和对应的残差（U/Uf=0.5）Fig.2 Plunge displacements obtained by Runge-Kutta method(RK)and precise integration method(PIM),where U/Uf=0.5

考虑在俯仰方向有立方非线性刚度，即G(ξ) =ξ，M(α) =α+ηα3，其中取η= 80。当无量纲风速超过Uf时，气动弹性系统会产生极限环振荡，如图3所示。可以看到，三种模型获得的结果完全一致。而当U/Uf大约等于2.25时，系统出现了二次分岔现象。对于这种现象，Liu和Dowell在相关工作中进行了深入的研究［6］。值得注意的是，三种模型的二次分岔结果也完全相同。此外，无论风速U/Uf在二次分岔临界值之前还是之后，三种模型的相图都是能够吻合的，如图4所示。

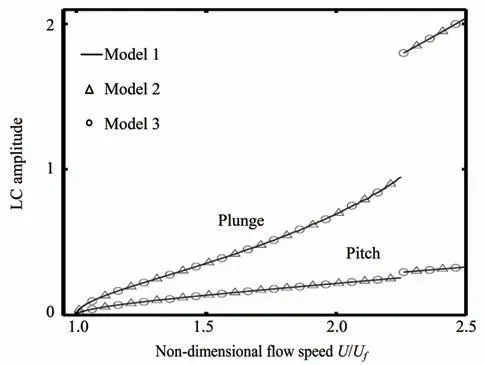
图3 考虑立方俯仰角刚度时RK法获得的不同模型的分岔图Fig.3 Bifurcation charts obtained by RK method as a cubic pitch stiffness is included

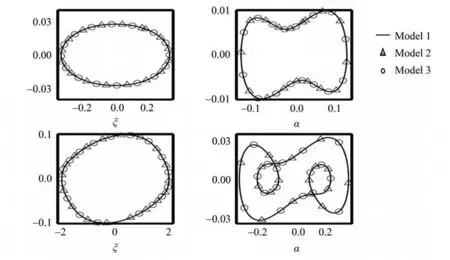
图4 考虑刚度立方非线性，在二次分岔前后的相图对比Fig.4 Comparison of the phase planes before or after the secondary bifurcation as a cubic pitch stiffness is included

考虑如下所示的分段线性

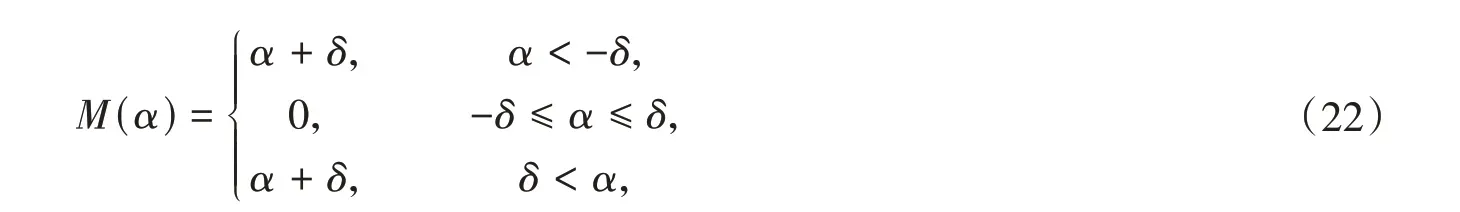
其中间隙参数设置为δ=0.5°. 通过RK 法得到的分岔如图5 所示。可以看到在大多数情况下，这三种模型的结果是相同的，但仍存在一些细微的差异。例如，当U/Uf= 0.31 时，模型1 与其他两个模型的结果不同。但从图6中可以看出，模型1的解与模型2的解是对称的。对于模型2，当U/Uf= 0.53时，以及模型3中U/Uf= 0.4时也出现了类似的现象。

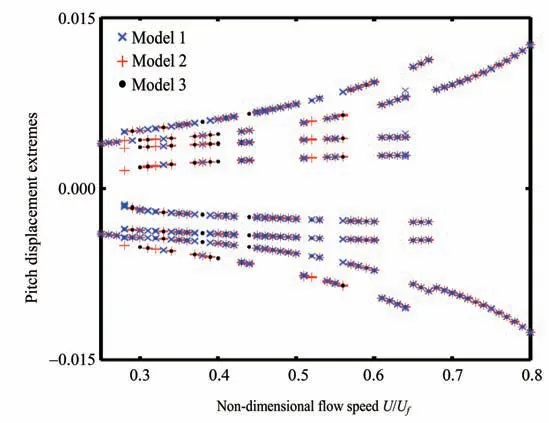
图5 在俯仰方向考虑分段线性，由RK法得到的不同模型的分岔图Fig.5 Bifurcation charts obtained by RK as a piecewise stiffness is included

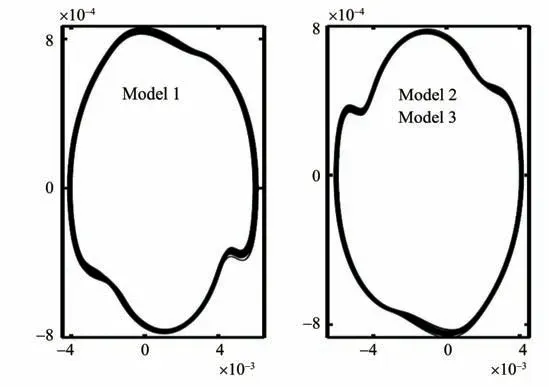
图6 考虑分段线性刚度，由RK法得到的不同模型沉浮方向的相图Fig.6 Phase plane in the plunge direction provided by RK method as a piecewise stiffness is included

事实上，这种现象是由分段线性系统在数值积分中，分段线性转换点不准引起的。早在20世纪90年代，Conner 等就阐述了这一数值现象［24］，此现象可以通过预测-校正的精细积分法来解决［23］。如图7 所示，通过精细积分法求解三种模型的数值解，分岔图就完全相同了。总而言之，对于含间隙非线性气动弹性系统，这三种模型也是等价的。

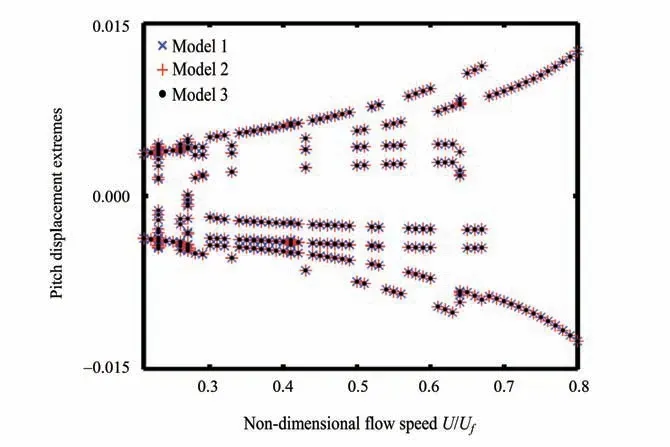
图7 考虑分段线性刚度时，精细积分法得到的不同模型的分岔图Fig.7 Bifurcation charts provided by PIM as a piecewise stiffness is included

4 结 论

由于Thordorsen函数中存在卷积积分，使得求解亚音速流作用下翼型气动弹性系统变得非常麻烦。其原因在于，卷积积分会使气动弹性系统同时出现积分算子和微分算子，这使得无法通过逐步积分法来直接求解。为了解决这一问题，研究人员陆续提出了一些化简方法来处理方程中的积分项。在已有的研究中，有三种广泛使用的状态空间化简模型。这些模型都可以成功处理系统中的积分项，其中模型1将气动弹性系统表示为8 个一阶常微分方程，其他模型由6 个常微分方程表示，本文从数学上和通过数值模拟，都证明了这三种状态空间模型在本质上是等价的。

此外，数值结果表明由于分段非线性的存在，这些模型在某些情况下通过RK法可能得到不同的数值结果。分析后发现，这些差异是由于数值积分过程中，气动弹性系统转换点不准确造成的。在本文中，通过将RK 法换成预估-校正的精细积分法，精确地确定转换点，从而解决了这个问题。并且三种模型得到完全相同的结果。

附录

参数ci和di：

式（3）中的矩阵和系数向量为

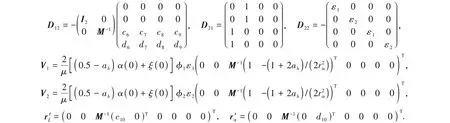
式（7）中的矩阵为

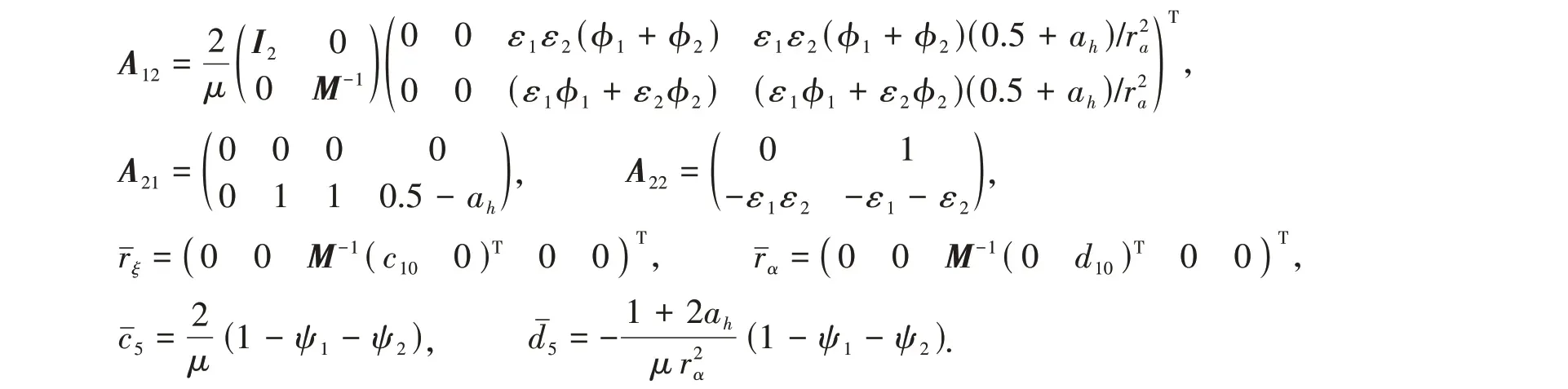
式（9）中的矩阵为