时间有限元的算法稳定性与周期延长率分析*
2022-06-08周宇汪利刘祚秋
周宇,汪利,刘祚秋
中山大学航空航天学院应用力学与工程系,广东 深圳 518107
时间有限元法是一种在时间域内用有限单元离散的Galerkin 算法。时间有限元法的发展可追溯到20 世纪60 年代末,时间有限元法一词最早于20世纪70年代被Clough提出[1],Fried及Argyris等最早作了这方面的工作[2]。时间有限元法由于其精度高、计算量适中等特点,在结构动力响应的数值分析领域得到了广泛应用。
在算法研究领域,Hulbert[3]建立了结构动力学方程的时间不连续Galerkin 有限元法,并证明了算法的稳定性和收敛性。随后Li 和Wiberg[4]研究了时间不连续Galerkin 有限元方法,提出了一种新的迭代求解算法。French 等[5-6]为求解二阶波动方程问题,提出了一种时间连续Galerkin 有限元方法。袁晓彬等[7]采用加权残值Galerkin法,建立了求解一阶线性微分方程组的全域时间有限元法。许伟等[8]基于五次Hermite 插值函数,构造了求解结构动力学二阶线性微分方程组的全域时间有限元算法。就在最近,Wang 和Zhong[9]构造出与传统的强控制方程形式等价的变分公式,以此建立了时间连续Galerkin有限元公式。
在算法实际应用方面,张方等[10]建立了动载荷识别的时间有限元模型,将时间有限元法应用到动载荷识别领域。荣吉利和李瑞英[11]用时间不连续Galerkin 法对水轮发电机轴系横向振动响应进行了仿真计算。隋永枫等[12]将时间有限元法扩展到陀螺系统,证明了算法的优越性。姜燕等[13]用时间有限元预测了铣削的稳定性,并用实验证明了时间有限元的有效性。
在作者最近的工作[9]中,已经给出了时间有限元严格的先验误差分析,并且发现与常规的Newmark法不同的是,时间有限元的计算误差不会随时间逐渐增大。这对工程计算十分重要,因为大部分算法中计算时间越长、误差越大。为了将时间有限元应用于工程分析,本文将进一步研究时间有限元的算法稳定性与周期延长率等,并通过梁的动力分析算例验证算法的精度。
1 时间有限元算法原理
在结构动力分析中,需要求解二阶常微分方程组
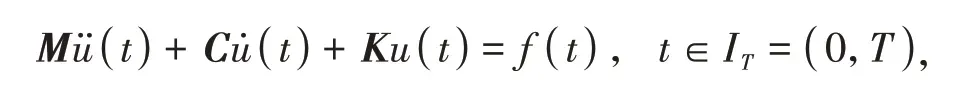
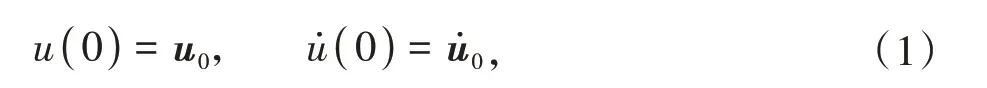
其中M为质量矩阵,C为粘滞阻尼矩阵,K为刚度矩阵,f为荷载向量,T为计算的时间长度,u,u̇分别为位移、速度,IT为时域区间。
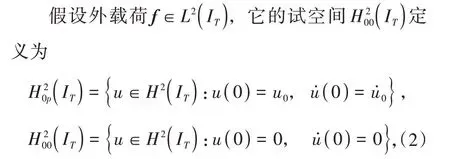
其中L2(IT)表示在区间上平方可积的函数,H2(IT)表示二阶导数平方可积函数。然后,建立结构动力问题的变分公式
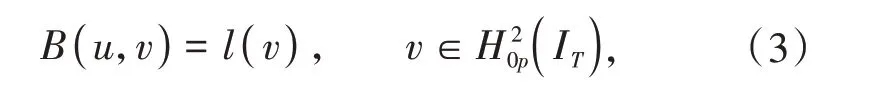
其中双线性泛函B:H2(IT) ×H2(IT) →R 和线性泛函l:H2(IT) →R表示为

有了位移响应函数,根据变分公式建立时间有限元方程
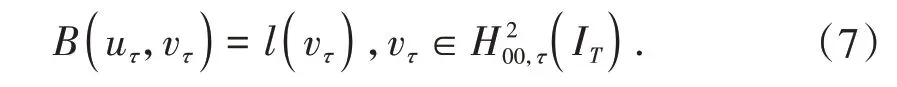
变分公式的具体推导过程以及时间有限元法的收敛性分析可参考文献[9]。然后,计算单元刚度矩阵Di和荷载向量{f}i
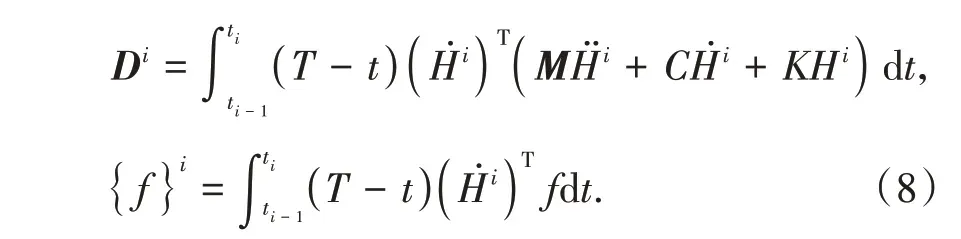
实际中,常采用高斯求积法计算Di和{f}i,最后通过组装得到整体代数方程

由于D是三阶对角块矩阵,在已知初始位移和速度的情况下,可用追赶法快速求解方程(9)。
2 算法的稳定性与周期延长率分析
2.1 稳定性分析
为分析时间有限元法的算法稳定性,针对自由振动问题(荷载f(t) = 0)建立的递推公式为[14]
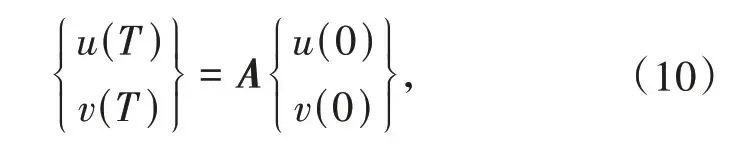
其中A为传递矩阵,要保证算法稳定,需满足
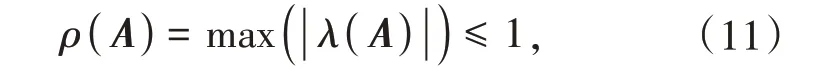
其中ρ(A)为谱半径,λ(A)为传递矩阵的特征值。

2.2 周期延长率
当系统存在一定的周期延长时,计算响应与实际响应将在长时间后存在周期错配,使得长期行为难以预测。周期延长率的计算公式为[15]
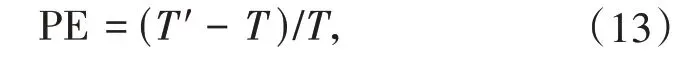
式中T为体系的理论自振周期;T′为数值解的振动周期。
实际分析中,得到的数值解并不是完美的简谐函数,如何获得数值解的周期是计算周期延长率的关键。采用随机子空间法[16],根据离散的位移数据直接找出周期。首先,对时间有限元的解插值得到间隔为Δt的位移值-u1,-u2,…,-un。然后,利用离散的位移值,构造一个Hankel矩阵,即
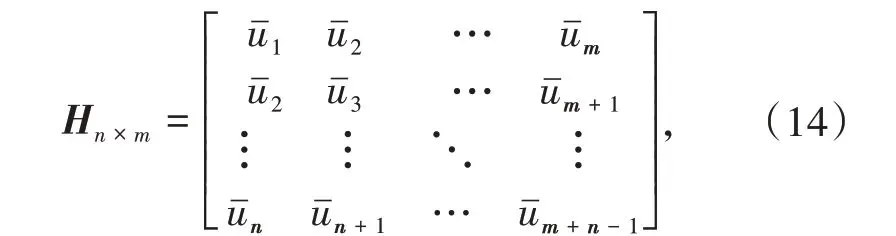
其中m+n为时间节点总个数。对矩阵H进行奇异值分解(SVD),得[17]
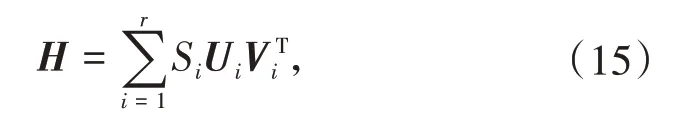
其中Si为H的奇异值,r为H的秩。根据随机子空间识别理论[16],得到离散系统特征矩阵Q,对Q进行特征值分解,得到特征值λ1,λ2,…,λn。最终,可得到离散数据的频率或周期

3 算例验证
考虑如下单自由度体系的自由振动问题
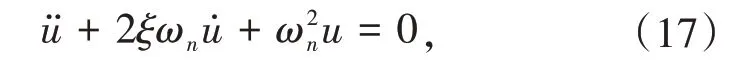
其中ξ为阻尼比,ωn为自振频率,Tn= 2π/ωn为系统周期,计算时长T=12 s.
一方面,进行算法的稳定性分析。主要考虑时间步长τ,阻尼比ξ,周期Tn(或频率)等因素的影响:1)固定τ= 0.25 s,阻尼比ξ=0~1%和不同周期Tn下,传递矩阵谱半径随步长周期比(τ/Tn)的变化见图1;2) 固定τ= 0.5 s,阻尼比ξ=0~1%和不同周期Tn下,传递矩阵谱半径随τ/Tn的变化见图2。可以看出,阻尼比ξ和τ/Tn显著影响谱半径的值;而给定ξ和τ/Tn,谱半径几乎与时间步长τ没有关系。当存在阻尼(ξ>0.05%)时,谱半径在合理的步长周期比范围(τ/Tn<1)内小于1,表明时间有限元计算是稳定的;而对于无阻尼或ξ<0.05%的系统,只有当τ/Tn<0.3时,谱半径小于1,此时属于条件稳定状态。
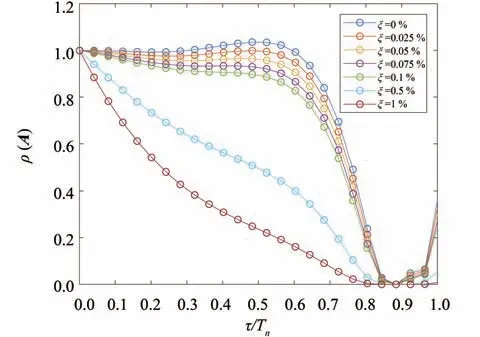
图1 τ=0.25时谱半径随阻尼比ξ和τ/Tn的变化Fig.1 Variation of spectral radius with damping ratio ξ and τ/Tn under τ=0.25
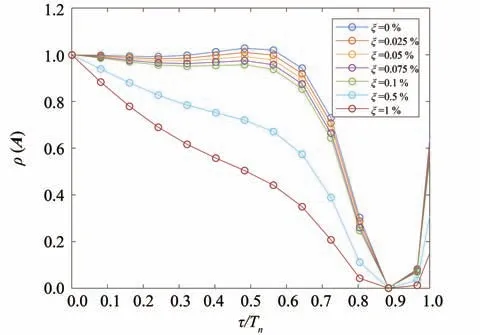
图2 τ=0.5时谱半径随阻尼比ξ和τ/Tn的变化Fig.2 Variation of spectral radius with damping ratio ξ and τ/Tn under τ=0.5
另一方面,为了研究时间有限元法的周期延长率,令阻尼比ξ为0,且固定系统周期为Tn= 4.考虑系统的初始位移为1、初始速度为0,此时位移响应的解析解为u(t) = cos(πt/2)。时间有限元法得到的计算结果见图3。从图中可以看出,改变时间步长基本不影响体系的计算振动周期,且计算振动周期与理论自振周期基本一致。为了对周期延长率进行定量分析,用随机子空间法得到计算数值解的工程频率fn,画出稳定图,如图4 所示。可以看出,当模型阶次为2时,随机子空间法便能得到满意的频率结果(接近0.25)。按照此思路,改变时间步长,取模型阶次为2,可得到周期延长率PE 随时间步长的变化曲线,如图5 所示。从图中可以看出,不同时间步长下,周期延长率几乎为0 (全小于0.01),表明时间有限元不会改变解的周期,在长时间计算中,不会引起周期错配。
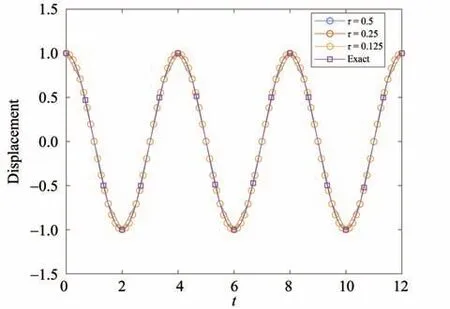
图3 不同时间步长时单自由度无阻尼自由振动系统的位移响应Fig.3 Displacement response of single degree of freedom undamped vibration system with different time steps
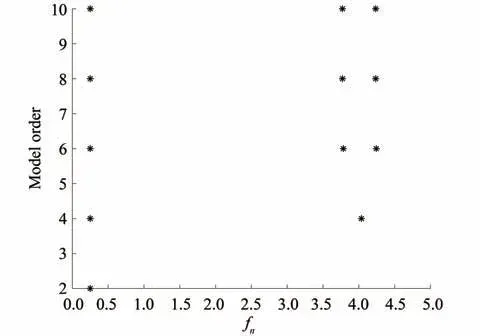
图4 随机子空间法的稳定图Fig.4 Stabilization diagram of stochastic subspace identification
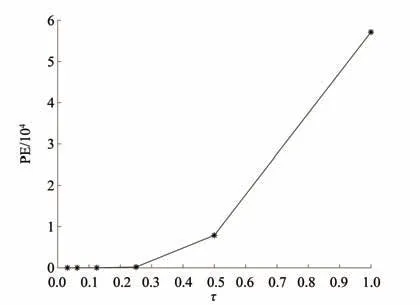
图5 周期延长率随时间步长的变化Fig.5 Change trend of period elongation with time step
4 应用于梁的振动分析
考虑承受集中荷载的等截面简支梁模型(如图6 所示)。荷载距左端支座的距离为s(s=L/4),大小为P(t) =Fsin(ωt)。研究的响应时间区间为[0,12],模型的基本参数是:质量分布m= 1 000 kg/m,梁长L= 10 m,弹性模量E= 3 × 109Pa,截面惯性矩I= 6 × 10-7m3,外荷载激振频率ω=π/2 rad/s以及荷载幅值F= 1 000 N。梁的初始横向位移和转角均设为0。为了建立梁的动力方程,首先对梁进行离散化,均匀划分为8个单元。选取结点的横向位移和转角为自由度,单元刚度矩阵为
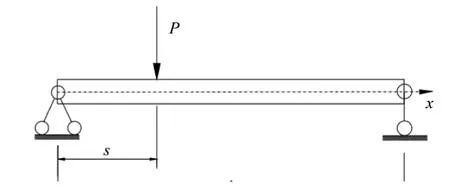
图6 受集中荷载的等截面简支梁模型Fig.6 Model of a beam with equal section under concentrated load
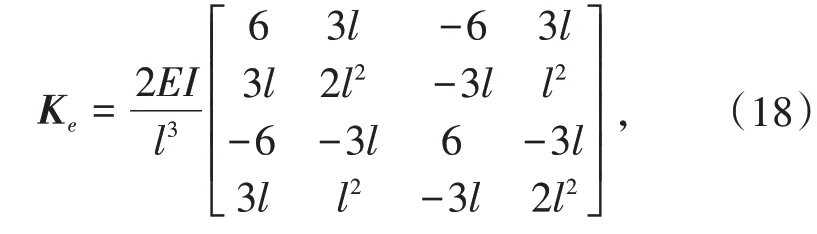
式中l是单元长度。类似的,单元质量矩阵为
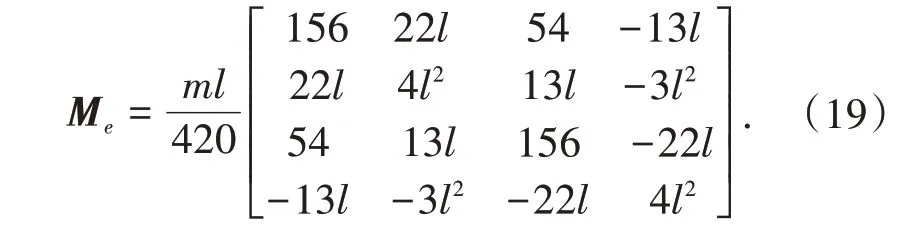
将单元刚度矩阵、质量矩阵和外力向量进行组装,集成结构体系的总体刚度矩阵K、质量矩阵M和外力荷载向量f(t),再采用阻尼理论假设得到体系的总体阻尼矩阵C,形成如式(1)的梁振动方程。然后,采用时间有限元法进行求解。
取跨中节点的横向位移为研究对象,可以得到跨中节点的横向位移的时间有限元解,如图7所示。从图中可以看出时间有限元的数值解与方程的解析解十分吻合。当然,为了对比,额外应用Newmark 法(γ=0.5,β=0.25) 对该问题进行求解。时间步长τ=1/8 下,时间有限元和Newmark 法在所有时间节点上位移和速度的逐点误差如图8和图9所示。从图中可以看出,时间有限元法的逐点误差明显比Newmark 法小。Newmark 法的误差会随着时间增加,而时间有限元的逐点误差却一直保持在较低的水平。
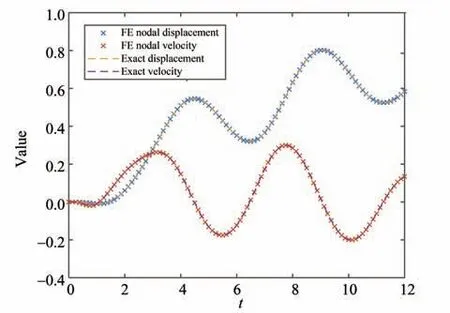
图7 τ=1/8时间有限元求解的跨中节点横向位移和速度响应Fig.7 Transverse displacement and velocity response of mid-span nodes solved by time finite element under τ=1/8
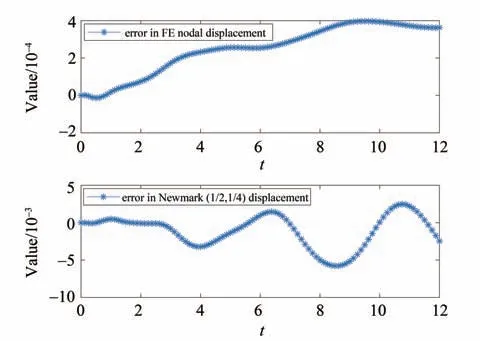
图8 时间有限元法和Newmark法的位移误差对比Fig.8 Comparison of errors in pointwise displacement by time FEM and Newmark method
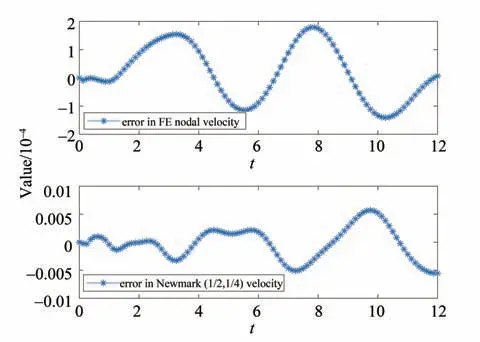
图9 时间有限元法和Newmark法的速度误差对比Fig.9 Comparison of errors in pointwise velocity by time FEM and Newmark method
为了量化计算误差,将时间有限元和Newmark法的位移和速度响应中的最大误差分别列于表1和表2中。可以看出,相同时间步长下,时间有限元法位移的最大误差仅为Newmark 法的6.67%~9.6%,速度误差不超过Newmark 法的5.78%。时间有限元法的精度显然比Newmark法高。
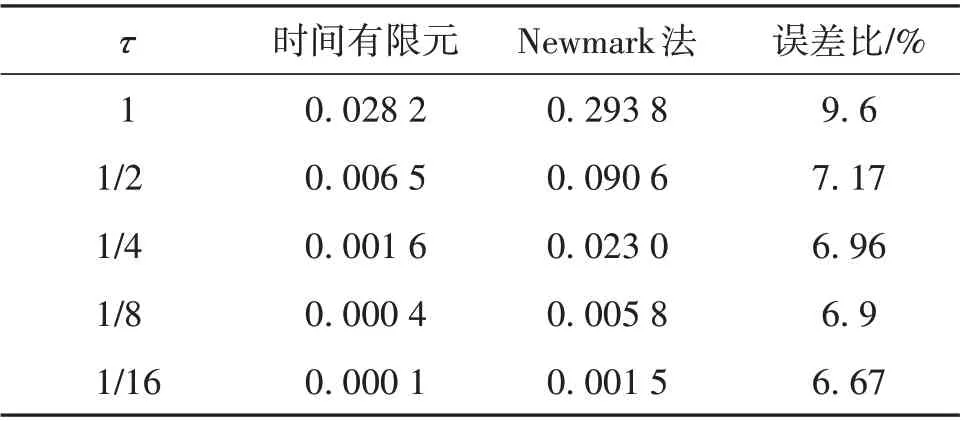
表1 时间有限元和Newmark法跨中位移的最大误差Table 1 Maximum error in mid-span displacement of time finite element and Newmark method
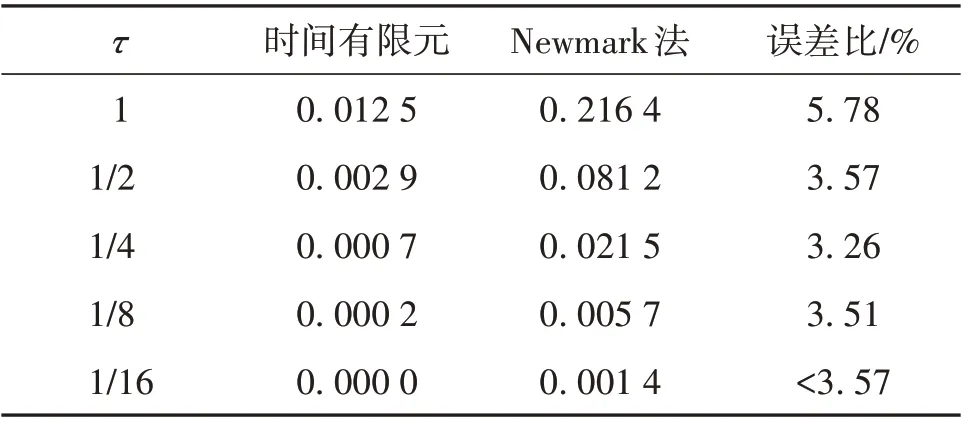
表2 时间有限元和Newmark法跨中速度的最大误差Table 2 Maximum error in mid-span velocity of time finite element and Newmark method
5 结 论
本文研究了时间有限元法的算法稳定性和周期延长率问题,得到了以下结论:
1) 对于有阻尼(阻尼比大于0.05%)单自由度系统,当ξ和τ/Tn<1 取不同值时,谱半径ρ(A)都始终小于1,表明时间有限元法的稳定性很好。对于无阻尼(或者阻尼比小于0.05%)单自由度系统,τ/Tn<0.3时系统达到条件稳定。
2) 时间有限元法的周期延长率(几乎)为0,可以认为计算振动周期等于理论自振周期,不存在周期延长的现象。
3) 时间有限元法在求解多自由度线性系统的动力反应问题时,其计算精度要远高于一般的Newmark法。
