王剑

[摘  要] 抛物线与直线综合题型常作为压轴题在中考中出现，该类问题往往条件信息众多，数形结合紧密. 问题突破建议深入分析问题条件的特点，立足知识考点开展思路突破. 同时注重解后反思，全面认识问题，强化解题方法. 文章以2021年连云港市的中考抛物线压轴题为例，开展解题探究，并提出了相应的教学建议.

[关键词] 抛物线;几何;面积;角度;拓展;转化

考题呈现，问题解读

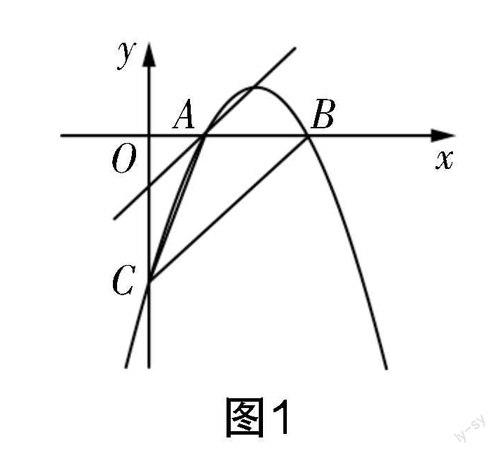
考题  （2021年江苏省连云港市中考卷第26题）如图1所示，抛物线y=mx2+（m2+3）x-（6m+9）与x轴交于点A和点B，与y轴交于点C，已知B（3，0）.

（1）求m的值和直线BC对应的函数解析式;

（2）P是抛物线上的一点，若S△PBC=S△ABC，请直接写出点P的坐标;

（3）Q为抛物线上的一点，若∠ACQ=45°，求点Q的坐标.

解读  本考题以抛物线与直线相交为背景，设定了抛物线与坐标轴的三个交点，第（1）问探求m的值和函数解析式，实则考查待定系数法;第（2）问和第（3）问则设定了抛物线上的点，构建了三角形和45°角，属于函数与几何的结合，实则考查学生在函数曲线中构建几何模型. 问题的综合性极强，对学生的逻辑推理、模型构建、转化运算能力有着较高的要求.

思维推理，过程突破

问题突破需要把握关键点，定位考点，结合知识点来构建模型，转化条件，准确运算，下面笔者逐问探究.

突破1：待定系数法求解析式

求抛物线解析式中的参数及直线BC的函数解析式的核心解法是待定系数法，因为抛物线的解析式为一般式，所以可以直接代入点的坐标求参数. 将点B（3，0）代入y=mx2+（m2+3）x-（6m+9）中，化简后可得m2+m=0，解得m=-1或m=0（舍去），所以抛物线的解析式为y=-x2+4x-3. 因为C为抛物线与y轴的交点，所以C（0，-3）.

设直线BC对应的函数解析式为y=kx+b，将点B和点C的坐标分别代入，可得3k+b=0，

b=-3，可解得k=1，

b=-3，所以直线BC对应的函数解析式为y=x-3.

突破2：等面积转化求坐标

该问设定P为抛物线上的点，求S△PBC =S△ABC时点P的坐标，而△ABC的三个顶点均为定点，故为固定的三角形，可直接结合面积公式来分析.

可将△ABC视为是以BC为底边，A为顶点的三角形，而△PBC为以BC为底边，P为顶点的三角形，则只需满足点P到直线BC的距离等于点A到直线BC的距离即可.

从几何视角来突破，利用“平行线之间的距离相等”来确定点P所在直线，有两种情形. 情形①为直线PA与直线BC相平行，此时点P位于直线BC的上方;情形②为点P所在直线与情形①中的直线PA关于直线BC对称，此时点P所在直线在BC的下方. 下面笔者结合几何知识求点P的坐标.

情形①——点P位于直线BC的上方

该情形为图2所示的直线P1A，设直线P1A的解析式为y=kx+b. 若P1A∥BC，则两直线解析式的k相等，即k=1. 由抛物线的解析式可知点A（1，0），B（3，0），将点A代入y=x+b中，可得y=x-1，联立直线与抛物线的解析式，可得点P1（2，1）.

情形②——点P位于直线BC的下方

该情形下点P所在直线应与抛物线有两个交点，如图2所示的点P2和P3，同理可知直线P2P3与BC平行，解析式中k=1. 对于其中的对称关系，可通过直线平移来实现，即直线P1A向下平移线段DC得到直线BC，再平移等长线段得到直线P2P3，故可推知CD=CE. 其中点D（0，-1），点C（0，-3），则CD=CE=2，所以点E的坐标为（0，-5）. 结合k=1及点E坐标可求得直线P2P3的解析式为y=x-5. 联立直线y=x-5与抛物线解析式，可求得点P2

，，P3

，.

综上可知，满足条件的点P有三个，分别为（2，1），

，

，

，.

突破3：模型构建求坐标

该问设定点Q为抛物线上的点，探究生成∠ACQ=45°时点Q的坐标，笔者采用数形结合的方法，构建几何模型，利用模型确定Q所在直线上的第2点，具体过程如下.

取点Q，连接CQ，过点A作CQ的垂线，垂足为D（如图3所示）. 过点D作DF⊥x轴于点F，再过点C作CE⊥FD交FD的延长线于点E，则图中存在“一线三直角”全等模型，由模型及∠ACQ=45°可知△CDE≌△DAF，由全等性质可得AF=DE，CE=DF.

可設DE=AF=a，则CE=DF=a+1，由OC=3可得DF=3-a，即a+1=3-a，可解得a=1，所以点D（2，-2）. 结合点C的坐标可得直线CD的解析式，即y=x-3. 联立直线CD与抛物线的解析式即可求点Q的坐标，即Q

，

-.

反思总结，解法拓展

1. 反思总结

上述对一道抛物线综合题进行了思路突破，整个过程充分把握问题特征，探索解法，下面笔者深入反思，赏析解法.

上述考题第（1）问的思维过程极具连贯性，可概括为“抛物线参数→点坐标→直线解析式”，即构建了“直线或曲线解析式?点的坐标”的推理关系，这也是待定系数求解的知识核心，该思维方法在函数综合题第（1）问求参数、点的坐标、解析式问题中应用广泛.

第（2）问可归为等面积问题，其突出特征是所涉两三角形可视为是同底三角形，该条件为上述平行或重合转化提供了基础. 而在求对称直线时所采用的平行构建策略，避免了繁复的代数运算，极大地简化了解题过程.

第（3）问给出特殊的45°角，同样求点的坐标，确定点所在直线的解析式是关键，上述基于45°角构建了“一线三直角”全等模型，利用模型特性来推导点坐标. 其中的等腰直角三角形、全等关系是该模型的核心，也是思路构建的关键.

2. 解法拓展

上述考题的第（3）问的思维过程可概括为：把握45°角→定位“一线三直角”全等模型→模型性质求线段→确定关键点坐标. 将“∠ACQ=45°”转化为模型中的特殊三角形，再由几何知识确定点坐标. 但其推理过程的难度较大，后续还需多步运算，实则可对模型进行简化，可避免无用计算.

以点A为圆心，AC长为半径画圆，再过点A作AC的垂线，与☉A的交点设为点D，过点D作x轴的垂线，垂足为F，如图4所示. 可知△ACD为等腰直角三角形，图中有“一线三直角”全等模型，可证△ADF≌△CAO，由全等性质可得AF=OC=3，DF=AO=1，从而可得点D（4，-1），可求得直线CD的解析式为y=x-3，直线CD与抛物线的交点就为点Q，直线与抛物线联立即可求得点Q的坐标为

，

-.

评析  上述“横向”构建了“一线三直角”全等模型，教师可直接利用线段长确定CQ所在直线上的点D的坐标，有效避免了线段长的推导. 其中的隐圆是实现等线段转化的重要策略，而构建垂直线段则呈现了特殊的模型.

解后反思，教学建议

上述对一道抛物线综合题进行了思路突破，充分呈现了解题的思维过程，有利于帮助学生掌握综合性问题的分析方法，下面笔者基于教学进一步反思.

1. 关注问题特点，分析转化策略

综合性问题的条件信息较为丰富，挖掘问题特点，开展条件转化是解题的关键环节，将直接影响解题思路的构建. 如上述第（2）问中给出了等面积条件，把握两三角形共底的特征，则可将问题转化为两线平行问题. 故解题教学要引导学生总结问题特点，提取条件特征，然后结合特征来转化问题. 同时问题条件的转化过程，也是对问题的本质探索. 常见的转化策略较多，除了上述平移转化等面积条件外，还有旋转转化、对称转化、线段截取转化等.

2. 立足问题条件，合理构建模型

数学模型在综合性问题中有着重要应用，模型的特征结论可降低思维难度，提升解题效率. 本题第（3）问中充分应用了“一线三直角”全等模型，利用模型呈现了45°角，并由模型结构推导了线段长，为后续的求解提供了条件. 实际教学中教师应注重数学模型的总结归纳，尤其是常用的几何模型，如“一线三等角”模型、“手拉手”模型、“将军饮马”模型、“半角”模型等. 引导学生关注模型特征，掌握模型结论的应用思路，丰富学生的知识储備.

3. 重视方法拓展，提升综合素养

上述考题来源于中考真题，问题的解法策略有着极高的应用价值，解题教学不仅要引导学生探索问题的常规解法，还应注重方法的拓展，如上述完成第（3）问的解法探究后，笔者进一步对模型进行了优化，使得学生可直接利用模型结论求关键点的坐标. 解法拓展不仅可以使学生深刻认识问题，丰富解题方法，还可以锻炼学生思维，提升学生的综合能力. 在实际探究中，建议教师立足优秀的中考真题，依托考题分析方法，思考方法的拓展方向. 同时注重学生的思维引导，给学生留足思考空间，以培养学生的综合素养为教学目标.