谭 旺，李 轶

（1.中国科学院重庆绿色智能技术研究院，重庆 400714；2.中国科学院大学计算机科学与技术学院，北京 101408）

0 引言

循环程序终止性的分析与验证已成为程序验证领域的一个热点问题，并且引起了国内外许多学者的关注［1-3］。循环程序的终止性是一个不可判定的问题［4-6］，它的解决方案可以广泛地提高软件的可靠性以及程序员的工作效率。目前有几种优秀的工具应用于不同计算模型的自动终止性验证分析［7-8］。证明给定循环程序是否是可终止的有着许多的研究方法，比如特征值法［9］、秩函数法［10-17］、界函数法［18-22］、抽象解释［23-25］以及不变式［26-27］等。

秩函数法作为终止性分析的主流方法已经得到了广泛的研究。当前求解秩函数的方法大多局限于线性秩函数［10-13］或者多项式秩函数［14-17］的求解。本文主要考虑给定循环的界函数计算问题，在循环程序体内设置一个循环计数器变量c，然后计算循环计数器变量的上界，不难看出，循环计数器变量的上界实际上就是某给定初始值的循环迭代次数的一个上界。如果对于任意满足循环条件的初始值，其对应的循环计数器变量均存在上界，那么该循环程序一定是可终止的。具体地，本文首先设定一个界函数模板并且将界函数的求解问题转化为线性二分类问题，然后利用支持向量机（Support Vector Machine，SVM）［28］探测分类超平面获得模板系数从而得到候选的界函数，最后将候选界函数进行优化并采用符号验证工具Redlog 对其进行验证。与基于秩函数的循环程序终止性验证问题相比，尽管计算循环程序计数器变量十分困难，即界函数方法是一个更为复杂的问题［29］，但是，本文的实验结果表明，对于某些不能通过计算线性秩函数或线性多阶段秩函数来证明其终止性的循环，通过本文方法却可以找到其线性界函数，从而证明这些循环的终止性。

1 预备知识

本文主要考虑如下形式循环，即：

其中：a=(a1，a2，…，ak)T∈Rk是一个k维向量，不等式≤0 是程序的循环条件，而=fi(a)中的表示ai在经过一次循环迭代后的值，并且=fi(a)是循环的赋值表达式，其中fi(a)是连续函数。

令a′=以及f(a)=(f1(a)，f2(a)，…，fk(a))T，因此，可得a′=f(a)。

例1 考虑以下来自文献［12］的循环：

在这个循环中，循环条件是4a1+a2≥1，循环区域为Ω={a∈R2：4a1+a2≥1}；赋值语句是=-2a1+4a2以及=4a1。

1.1 界函数

如果一个循环程序在满足循环条件内的所有初始值上均是可终止的，那么该循环程序便是可终止程序。对于可终止循环程序，满足循环条件的初始点在有限次迭代之后必然跳出Ω。给定一个可终止循环P，令C(a)：Ω→N 为初始值输入点a在循环P中的有穷次迭代次数。为方便，本文称C(a)为Ω（或程序P）的迭代次数函数。对∀a∈Ω，有C(a)≥1。

一般地，要精确计算C(a)是困难的。为此引入界函数的概念来逼近C(a)。函数的定义如下：

定义1给定循环程序P。令C(a)为程序P上的迭代次数函数。如果存在函数τ(a)，使得∀a∈Ω，有τ(a)≥C(a)，则称τ(a)为程序P的界函数。

从定义可以看出，对一个循环程序，若能够求解出其对应的界函数，那么初始值的迭代次数均会有一上界（即：该初始值必在有穷次迭代后跳出Ω）。因此，如果任意初始值a∈Ω均能够在有穷次迭代后跳出Ω，那么该循环程序就是终止的。

1.2 支持向量机

支持向量机［30］是一种对数据进行二元分类的广义线性分类器，提出后便得到了广泛的关注和持续的发展。此外，由于支持向量机方法已经逐步理论化并成为统计学习理论的一部分［31］，并且是建立在结构风险最小原理基础上的，因此，其坚实的理论基础以及良好的特性使得现在很多领域都对其有着广泛的应用，例如：模式识别、概率密度估计和回归估计等。本文将界函数计算问题归结为线性二分类问题，从而可以利用支持向量机探测候选界函数。

假设给定训练样本集D={(x1，y1)，(x2，y2)，…，(xk，yk)}，其中yi∈{-1，+1}。样本空间的划分问题即是否能够找到一个超平面wTx+b=0 使得这两类点分离，其中：w为法向量，决定了超平面的方向，而b则是位移项。支持向量机算法的作用便是能够找到向量w以及实数b使得(xi，yi)∈D满足［32］：

特别地，支持向量机能够找到向量w使得：

1.3 不变式

程序不变式指的是程序变量之间满足的并且不随程序状态迁移发生变化的关系。当前，线性循环不变式以及多项式循环不变式的生成都取得了很大的进展，构造程序不变式已成为软件自动验证领域内的重要研究内容。程序不变式的一般定义如下：

定义2给定带初始值的循环程序P0：

如果存在表达式I(a)满足下列两个条件：

那么，I(a)称为循环P0的循环不变式。其中：θ表示初始点集合；initial 条件表明循环的第一次迭代前，循环不变式为真；consecutive 条件表明如果在循环体内某次迭代前为真，那么迭代后仍保持为真。

2 界函数的合成

本章描述了循环程序界函数的合成方法，主要包括了如何将合成界函数的问题转换为分类问题，如何构建训练集，如何获得分类超平面来确定候选界函数，如何对候选界函数进行优化，以及如何构建测试集。

2.1 问题转换

本节将会介绍如何将界函数的求解问题转化为分类问题。

令a=(a1，a2，…，ak)T∈Rk，其中k为Ω中点的维数。令τ(a)=wT·V(a)为循环程序P的界函数，其中wT为参数。τ(a)便是所设置的界函数模板，其中，V(a)由单项式或多项式所构成。

根据迭代函数的定义，可得

又由界函数的定义，有

也即：对∀a∈Ω，可得

故∀a∈Ω，可得

综上所述，界函数的计算问题可以被归结为负类点u-与集合T的超平面划分问题，而这是一个典型的二分类问题。由于T是无穷点集，为了便于利用SVM 去求解该超平面，需要首先从T中抽取有限个样本点构成T0，故负类点u-与集合T的超平面划分问题便被转化为u-与集合T0的超平面划分问题。若u-与有限点集T0之间的超平面一旦被计算，就可以得到了一个“候选的界函数”，然后利用Redlog 工具去验证该候选界函数是否是真的界函数。

例2 考虑例1 所示循环。

本例中设置其界函数模板为：

τ(a1，a2)=w1·(a1+1)2+w2·(a2+1)2+w3

即：

由T的定义，

故可得两类点集合为：

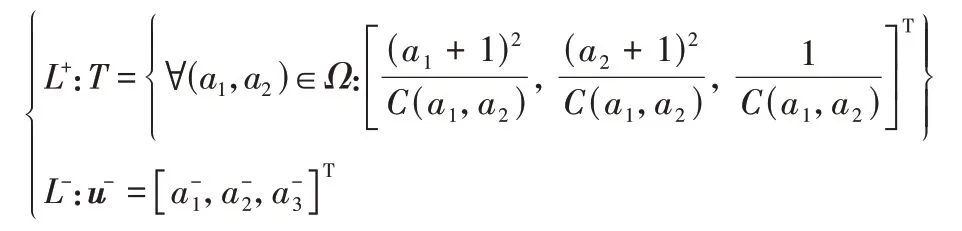
即：本文需要找到一个线性超平面L(u)：=wT·u=0 将u-与集合T严格分离。

2.2 超平面的求解

从2.1 节可知，本文将候选界函数的求解问题转化为一个u-与T0之间的二分类问题，即找到u-与T0之间的超平面L(u)：=wT·u=0，从而获得候选界函数的系数wT，进而得到候选的界函数τ(a)=wT·V(a)。为此，本文首先需要构造训练集，而构造训练集的一般过程分为两步：一是构造正类点集合T0和负类点u-；二是对所获得的样本点打上标签。过程如下：

1）正类点集合T0和负类点u-。

首先需要在循环区域Ω中自定义采样区间并采n个样本点，即针对每一个变量自定义取值范围，其中i∈{1，2，…，k}，而这里的以及n为可调参数；然后针对每一个采样点，求解出其精确迭代次数，之后通过T=映射到U空间，本文将该映射关系令为H，这样便获得了正类点集合T0，其次，还需要找到一个负类点u-，满足u-∉T，而实验中只需要找到一个这样的点作为负类点即可。这样的点是容易选取的。

例3 考虑例1 中的循环（续例2）。

由于该循环的循环区域Ω为：4a1+a2≥1，因此需要在像空间U空间外找寻一个样本点作为反例点u-。本例中选取反例点为（0，0，1）。由于该循环区域Ω为无界区域，因此为构造样本集T0需要在Ω中自定义一个有界的采样区间进行采样，这里设定采样区间为a1∈(-100，100) 以及a2∈（-100，100）。

2）打标签。

在得到样本点之后，还需要对样本点打上标签，正例点打上+1，负例点打上-1。

算法1 描述了求解样本点真实迭代次数的过程，针对某一给定样本点以及循环程序，求解出该样本点在循环程序中的迭代次数。

算法2 描述了训练集的构建过程。首先确定采样个数，然后针对所采样本点用上述的映射关系映射到U空间得到集合T0，之后选取一负类点u-使之满足u-∈L-，最后分别对正类点以及负类点打上标签。

在得到训练集xtrain以及ytrain之后，便可以通过SVM 进行训练。从上述构造训练集的过程可以看出，无论所选取的界函数模板为何形式，都可以将样本点映射到U空间，使得界函数的计算问题可以直接转化为一个线性二分类问题。因此在利用SVM 的训练过程中均采用线性核函数，在用训练集进行训练之后，所求得超平面如下：

且对∀(u1，u2，…，ud)∈T0，有

若1-wd+1>0，则由式（9），对∀(u1，u2，…，ud)∈T0，有

可得到一个新的超平面L(u)=WT·u，且对∀u∈T0，有L(u)≥1，即T0在L(u)的正半部分。

当1-wd+1<0 时，将重新构建训练集进行训练。

因此根据事先设定的模板，便可以得到候选界函数为：

例4 对于例1 中的循环程序（续接例3）。

将例3 所得到的训练集代入SVM 模型进行训练之后，可以得到分类超平面系数为：

因此可以得到：

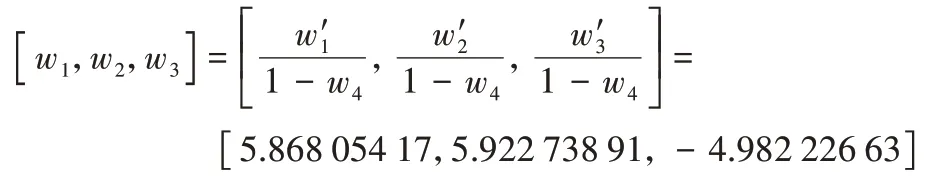
则候选界函数为：

τ(a1，a2)=5.868 054 17(a1+1)2+5.922 738 91(a2+1)2-4.982 226 63

2.3 候选界函数的优化

通过上述对超平面的求解，可以得到界函数的模板系数，进而得到候选的界函数。此外，根据界函数自身独特的性质，可以对候选界函数通过一些方法进行优化，使其有更大的可能通过后续的精确验证。

根据界函数的性质，界函数满足：∀a∈Ω，τ(a)≥C(a)。因此，本文将候选的界函数进行放大操作得到τ′(a)，使其满足：

因此，如果能够通过优化得到τ′(a)，那么本文最终只需验证τ′(a)是否是真正的界函数，即验证τ′(a)≥C(a)。

本文将分为以下几个情况对候选τ(a)进行处理：

1）令出现在τ(a)中的程序变量集S={}，其中ij∈{1，2，…，k}。如果存在ij，使得在Ω上恒为正或者恒为负，那么就可以将这种情形下的τ(a)进行优化放大处理。

3）对于候选界函数中的常数项，可以始终对其进行放大处理：一是当所求的常数项范围在（-1，1），可以直接将其放大至1；二是当所求的常数项范围为(-∞，-1)，将其上取整再取平方值。通过放大常数项系数，使得候选的界函数有更大的可能通过后续的验证。

例5 考虑例1 中的循环，续接例4。

由于其程序变量在Ω上有正有负，所以将该程序变量在模板中系数设为2，由设置的界函数模板易得，变量项(a1+1)2与(a2+1)2均为正项，因此其系数可以进行放大处理（如：向上取整）。

根据例4 所得的超平面系数，可以得到候选界函数为，

τ(a1，a2)=5.868 054 17(a1+1)2+5.922 738 91(a2+1)2-4.982 226 63

于是将所得的候选界函数变量项前的系数进行向上取整，可得：

τ′(a1，a2)=6(a1+1)2+6(a2+1)2-4.982 226 63

再对常数项进行处理，可得最终的候选界函数为：

τ″(a1，a2)=6(a1+1)2+6(a2+1)2+25

2.4 测试集

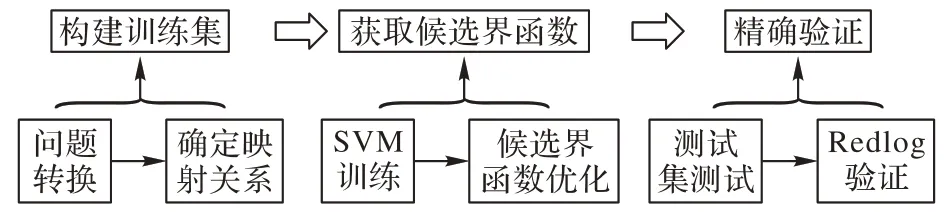
在得到候选的界函数之后，还需要在精确验证前构造一个测试集对其进行初步的验证，当所获得的候选界函数没能够通过测试集时，可以将未通过的测试样本点添加进入训练集，然后再重新训练，或者可以通过调整负类点的值，再进行训练。测试集构造过程如下：本文将上述所得的候选界函数称为candidate_BF，在循环条件围成的区域Ω中随机抽取采样点若干次。然后针对每一个样本点代入candidate_BF求解得到该样本点的迭代次数上界c_cal。最后着代入C(a)求解其真实的迭代次数c_real，若出现c_cal

3 精确验证

本章将介绍如何对上述所得的候选界函数进行进一步的精确验证。得到候选界函数之后，并且该函数已经通过测试集验证，但测试集仅是离散的样本点，远远不能表征整个循环区域Ω，因此，还需要对其进行进一步的精确验证以保证所得到的候选界函数在整个Ω内满足界函数的性质。本文采用的方法是：首先找出循环中的不变式，然后通过不变式以及工具Redlog 去验证所得到的函数是否满足界函数的性质。

3.1 不变式的构建

构建不变式，首先需要设定不变式的模板，本文不变式的模板与前述提及的界函数模板保持一致。假定不变式为I(a，c)：=MT·V(a)≥c，其中MT=(m1，m2，…，md)为参数，c为程序的计数变量用于计算迭代次数。根据不变式的性质，可得：

能够同时满足A、B 两式的表达式便是该循环的不变式，令A 式中MT以及a*需要满足的范围为M0，采用Redlog 工具对B 式进行量词消去（Quantifier Elimination，QE），消去(a，c)，可以得到不变式模板系数MT需要满足的范围M1。其中，a*为初始输入，本文将其参数化。

3.2 候选界函数的验证

构建不变式是为了利用不变式来验证候选界函数，如果该循环存在一个不变式能够推出候选界函数为真，那么该候选界函数就为真正的界函数。基于此，可得：

采用Redlog 工具对式（14）进行量词消去，消去(a，c)，可以得到式（14）中MT以及a*需要满足范围M2。

综上：对两次所得到的MT范围求交，判断是否存在一组MT，使其满足A、B、C 三式。因此，可得：

同样采用Redlog 工具对式（15）进行量词消去，消去MT，可以得到满足式（15）中a*需要满足的范围M3。对满足M3的初始值a*必存在一组MT使得该循环存在一个不变式I(a，c)：=MT·V(a)≥c，该不变式能够蕴含候选界函数。

因此最终还需要验证是否对于整个循环区域内的初始点都存在一个不变式，使得该不变式能够推出候选界函数为真，即验证是否循环区域Ω都在M3内部。

依然采用Redlog 工具对式（16）进行量词消去，消去a*，若最终输出结果为真，那么表示整个循环区域内的点均能够找到一个与之对应的不变式，并且该不变式能够蕴含候选界函数。

综上所述，利用Redlog 工具借助不变式验证候选界函数的算法如下：

本文在求解候选界函数时并不局限于函数的形式，超越函数、多项式函数均可，但是由于后期验证依赖于Redlog 工具，而由于Redlog 工具本身的局限性，导致它无法处理一些高次的多项式函数以及超越函数，因此对这类候选界函数Redlog 无法进行验证，这也是本文循环程序界函数计算方法的局限所在。综上所述，求解某给定循环其对应的界函数的过程框架如图1 所示。

图1 界函数合成框架Fig.1 Framework of synthesizing loop bound function

其中在通过SVM 获取候选超平面时，由于本文将界函数的计算问题转化为线性二分类问题，因此在SVM 训练时均采用线性核函数。此外，并非所有的循环经过一次训练就可以直接通过测试集，因此当第一次训练后的候选界函数并未通过测试集时，将测试集中未通过的点重新加入训练集进行训练，然后自行设定训练次数，重复上述过程。整个实验流程如图2 所示。

图2 基于SVM的循环程序界函数计算流程Fig.2 Flowchart of calculating loop bound function for loop program via SVM

综上所述，算法5 描述了对于给定循环程序，其界函数计算过程如下：首先设定界函数的模板从而得到映射关系，然后调用算法2 构建训练集，得到训练集利用SVM 进行训练得到分类超平面进而得到候选的界函数，再对该候选界函数进行优化得到新的候选界函数，之后通过算法3 利用测试集对该候选界函数进行初步验证，最后利用算法4 对通过测试集验证的候选界函数利用Redlog 工具进行精确验证，如果验证通过，那么该候选界函数便是该循环程序的真正的界函数。

4 实验与结果分析

本文求解候选界函数是通过Python 利用Scikit-learn［28］包进行实现，并且所有的实验均基于2.9 GHz Intel Core i5-9400f CPU 和8 GB 2 666 MHz DDR4 RAM 的PC 上进行的。

4.1 实验结果

所有循环均取自于两种方式：一是现有其他文献工作中的循环；二是在现有文献工作中的循环基础上进行了修改。表1 列出了本次实验所涉及的循环，其中循环1～2 来自于界函数相关文献［21-22］中所提及的循环，循环3～6 来自于秩函数相关文献［17］中的循环，循环7～9 则是对秩函数相关文献中循环基础上作出了修改，循环10 则是取自于文献［12］。

表1 实验所涉及的循环Tab.1 Loops for experiments

从表2 可以看出：不同的循环有着各自不同的模板，并且不同的循环其所选取的负类点的值也各不相同。此外，还可以看出，针对从界函数文献中提取的循环1～2，本文方法能够获得该循环所对应的界函数；针对从秩函数文献中获得的循环3～6，本文方法能够对这些循环求解其对应的界函数；针对循环7～9，当前求解秩函数方法不能获取其线性秩函数，只能够求解其多阶段线性秩函数，但是本文方法却能够获得其全局的线性界函数；针对循环10，对比方法不能得到其线性秩函数以及多阶段线性秩函数，本文方法也能获得其对应的界函数。

表2 实验参数以及所得模板系数Tab.2 Experimental parameters and template coefficients

4.2 实验对比

对于上述10 个循环将本文方法与当前循环程序终止性验证的主流方法秩函数法作出对比以及与界函数相关方法作出比较。

4.2.1 与秩函数法的对比

秩函数是程序终止性验证的主流方法，因此首先选取了三种当前合成秩函数的方法与本文方法在可行性以及合成秩函数或者界函数形式这两个方面作出对比。表3 描述了针对表1 的循环程序，基于量词消去秩函数合成、基于SVM秩函数合成以及多阶段秩函数合成方法与本文方法的实验结果。

从表3 的实验结果可以看出：

表3 不同方法的可行性对比Tab.3 Feasibility comparison of different methods

1）基于QE 的方法由于其运算复杂度高，因此一般用于处理线性循环，无法处理多阶的循环程序，而本文方法可以处理多阶的循环程序。

2）基于SVM 的秩函数合成方法其本身需要设定秩函数模板，再求解模板系数的值，因此对于一些存在多阶段秩函数的循环程序便无法合成，而本文界函数方法可以合成全局的界函数。

3）基于线性规划的多阶段线性秩函数合成，它本身只能针对单路径线性约束循环程序，对于一些二次或高次的循环程序便不能合成对应的秩函数。

综上所述，针对表1 所述的循环程序，在可行性上，本文方法能够处理更多的循环。接下来将上述三种秩函数所能得到的秩函数形式与本文方法所能得到的界函数形式进行对比，表4 罗列了针对表1 的循环，秩函数方法所能合成的秩函数形式以及本文方法所能得到的界函数形式。

表4 实验所得函数形式结果对比Tab.4 Comparison of experimental results in functional forms

从表4 可以看出，与三种秩函数的合成方法所求解得到的秩函数形式相比，本文方法求解得到的界函数在形式上更加简洁并且所得到的界函数均为全局界函数。

1）针对循环5～6，基于SVM 的方法虽然能够得到秩函数，但是秩函数形式是非线性的，而本文方法却能够求解得到其所对应的线性界函数，相较于非线性模板，线性模板在模板的选取上更加简洁直接。

2）针对循环7～9，此类循环没有线性秩函数，仅仅存在多阶段线性秩函数。本次实验多阶段秩函数的求解过程采用了irankfinder 工具进行实验，并将本文方法与文献［12］中的求解多阶段线性秩函数合成法进行对比，从表4 结果可以看出，文献［12］方法无法求解得到该循环所对应的全局线性秩函数，仅仅能够获得多阶段的线性秩函数，但是本文方法却可以得到全局的线性界函数。

3）针对循环10，该循环利用秩函数求解方法，无法获取其线性秩函数以及多阶段线性秩函数，但是本文方法却能够求解其非线性的界函数。此外，实验中设置了简单的模板尝试求解循环12 的2 次秩函数，但通过计算发现没有相应的秩函数（倘若设置复杂的2 次模板，则超出了工具的计算能力）。

综上所述，针对表1 所述的循环程序，与当前的三种秩函数的合成方法相比较，本文界函数方法不仅能够处理更多的循环，并且还有着以下的特点：一是对某些循环，秩函数法仅能够获取非线性的秩函数，但是本文界函数法能够获取线性的界函数，相较于非线性结构，线性结构更为简洁；二是对某些循环，秩函数法仅仅能够求解多阶段的线性秩函数，但是本文界函数法能够得到全局的界函数；三是对某些循环，秩函数方法无法求解得到其对应的线性秩函数或者多阶段线性秩函数，但是本文方法能够获得其非线性的界函数。

4.2.2 与界函数法的对比

相较于现有界函数求解方法，本文提出了一个新的界函数求解思路，即将界函数的求解问题转化为线性的二分类问题，然后利用SVM 得到分类超平面进而求解得到模板系数。因此本文方法求解候选界函数的过程并不局限于循环程序的形式，循环程序可以是多项式或者非多项式。此外，对于候选界函数的证明过程，本文给出了一个更加具有完备性的验证过程：

1）文献［18-19，22］中的方法所针对的循环并非将初始值全部作为参数，而是给定具体的初始值或者给定部分初始值；本文方法所针对的循环程序是将初始值作为参数的循环。

2）文献［21］方法在验证候选界函数时也需要获取不变式，该方法首先将不变式的求解转化为二次规划优化问题，再利用现有求解器获取候选的不变式，最后验证该候选不变式是否为真正的不变式；而本文方法则是利用符号计算，在不变式参数全空间对满足条件的不变式进行查找，因此相较于文献［21］方法，本文方法更加完备。例如：针对循环1，文献［21］方法需要首先求解得到候选的不变式为a1+a2-≥c，然后再验证该不变式是否为真正的不变式，而与之不同的是本文方法采用符号计算在不变式参数全空间去寻找满足条件的不变式，因此并不需要求解得到具体的不变式，仅需考虑其存在性。

5 结语

本文将界函数的求解问题转化为线性二分类问题，提出了一个新的方法去寻找循环程序的界函数。首先，设定一个界函数模板，然后利用SVM 查找分类超平面获取模板系数从而得到候选的界函数，最后通过现有符号验证工具Redlog结合不变式精确验证其是否是一个正确的界函数。从实验结果可以看出，相较于当前的秩函数相关方法，针对循环5～6，秩函数方法只能够找到其非线性的秩函数，但本文方法能够得到其对应的线性界函数；针对循环7～9，该循环没有对应的线性秩函数，只有多阶段线性秩函数，但是本文方法能够得到其对应的全局线性界函数；针对循环10，当前秩函数方法不能得到其对应的线性秩函数以及多阶段线性秩函数，而本文方法能够得到其对应2 次界函数。但是，后期的验证过程仍然依赖于Redlog 工具，因此对于一些循环利用本文方法即使能够获得其候选的界函数，但是由于Redlog 工具计算能力的局限性，不能对其进行验证。此外，如何更加有效率地选取界函数模板以及训练集中的负类点也是在未来工作中需要进一步深入研究的问题。