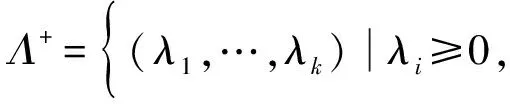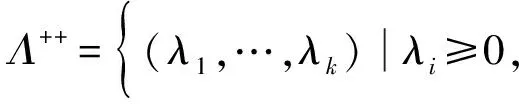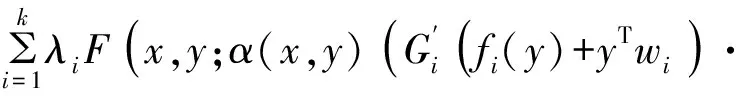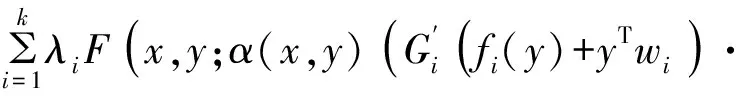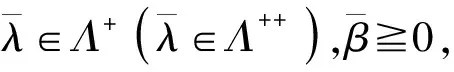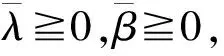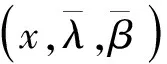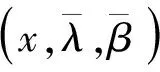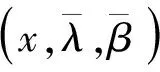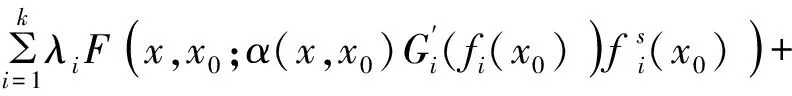一类凸多目标半无限规划的Mond-Weir型对偶
2022-01-11简相栋王文东甄艳秋
简相栋,王文东,甄艳秋
(延安大学 数学与计算机科学学院,陕西 延安 716000)
利用广义凸函数研究数学规划中的对偶问题一直是凸规划中一个非常重要的研究内容。文献[1,2]提出了一类新的广义凸函数即G-不变凸,同时在这些新的广义凸性条件下研究了一类多目标规划问题的最优性与对偶性,随后赵洁等在文献[3-7]中研究了一类带有支撑函数的多目标规划问题的对偶性。本文在以上文献的基础上,借助次线性泛函的性质[8]和Minch对称梯度[9]将广义凸性进行推广,建立研究了一类带有支撑函数的多目标规划问题的Mond-Weir型对偶问题,结合K-T最优性必要条件证明得到了一些弱对偶定理、强对偶定理以及严格逆对偶定理,改进和推广了文献[3-7]的结果。
1 基本定义
定义1[8](次线性函数)设F:X×X×Rn→R是关于第三变元的次线性函数,如果满足对于∀x1,∀x2∈X,有
F(x1,x2;α1+α2)≤F(x1,x2;α1)+(x1,x2;α2),
∀α1,α2∈Rn;
F(x1,x2;rα)=rF(x1,x2;α),∀r∈R+,α∈Rn。
定义2[10]如果有f(x+h)-f(x-h)=2hTfs(x)+o(‖h‖),称函数f(x)在x是对称梯度,并记作
fs(x)。
定义3[11]设x0∈X,如果不存在x∈X,使得
f(x) 定义4 如果存在α:Rn×Rn→R+{0},i=1,…,k,∀εi>0,使得对于x∈X,i=1,…,k有 则称(fi(x)+xTwi)在x∈X处是广义对称G-(F,α,ε)-凸函数。 定义5 如果存在α:Rn×Rn→R+{0},i=1,…,k,∀εi>0,使得对于x∈X,i=1,…,k有 则称(fi(x)+xTwi)在x∈X处是广义对称G-(F,α,ε)-拟凸函数。 定义6 如果存在α:Rn×Rn→R+{0},i=1,…,k,∀εi>0,使得对于x∈X,i=1,…,k有 则称(fi(x)+xTwi)在x∈K处是广义对称G-(F,α,ε)-伪凸函数。 考虑下面多目标半无限规划 其中f=(f1,f2,…,fk):X→Rk以及g:X×U→Rm对于∀u∈U是定义在X上的对称函数,X⊂Rn是一非空开子集,U⊂Rm是一个无限参数集。令K={1,2,3,…,k},M={1,2,3,…,m},Ifi(x),i=1,…,k表示fi的值,Ci是Rn中对于每一个i∈K,j∈M的紧凸集,记X0={X∈X|g(x,uj)0,X⊂Rm}为(MP)的可行解集,U*={uj|j∈△,J(x0)⊂△是相应指标集}是U的任意可数子集,△={j|g(x,u)0,x∈X0,uj∈U},J(x0)={j|g(x0,uj)=0},函数G=(G1,…,Gk):R→RK,每一个Gi:Ifi(x)→R,i=1,…,k是严格单调递增的可微实值函数。s(x|Ci)表示X上的支撑函数,其定义如下: s(x|Ci)=max{〈wi,x〉|wi∈Ci},i∈K。 对于(MP)问题,其Mond-Weir型对偶规划如下: K-T-(必要条件): 定理1 (弱对偶)假设x,(y,λ,β)分别是问题(MP)和问题(DMP)的可行解,如果满足下列条件: (i)fi在y处是广义对称G-(F,α,ε)-凸函数; (ii)g(x,uj)在y处是广义对称G-(F,α,ε)-凸函数; (iv)s(x|Ci)=xTwi,wi∈Ci,i∈K, s(y|Ci)=yTwi,wi∈Ci,i∈K。 则F(x)≮G(y)。 证明反证法。假设 F(x) fi(x)+s(x|Ci), 由条件(iv)得fi(x)+xTwi 又因为函数G=(G1,…,Gk):R→Rk,每一个Gi:Ifi(x)→R,i=1,…,k是严格单调递增的可微实值函数,则有 G(fi(x)+xTwi) 由条件(i)结合上式可知 上式两边同乘以λi再求和得 (1) 又因为条件(ii)可得 Gj(g(x,uj))-Gj(g(y,uj)) (2) 给(2)式两边同时乘以β1并且求和可得 (3) 因为设x是规划(MP)的任一可行解,(y,λ,β)是规划(DMP)的可行解,则 g(x,uj)g(y,uj),j∈△。 由于每一个Gi,j∈△是严格单调递增的可微实值函数,所以有 Gj(g(x,uj))Gj(g(y,uj)),j∈△。 由条件(ii)中bj>0和条件(iv)知 j∈△。 结合(3)式知 (4) 将(1)式和(2)式相加结合条件(iii)整理得 (5) 由F的性质以及K-T条件知 这与(5)式矛盾,故F(x)≮G(y)。 定理2 (弱对偶)假设x,(y,λ,β)分别是问题(MP)和问题(DMP)的可行解,如果满足下列条件: (i)fi在y处是广义对称G-(F,α,ε)-伪凸函数; (ii)g(x,uj)在y处是广义对称G-(F,α,ε)-拟凸函数; (iv)s(x|Ci)=xTwi,wi∈Ci,i∈K, s(y|Ci)=yTwi,wi∈Ci,i∈K。 则F(x)≮G(y)。 证明反证法。假设 F(x) fi(x)+s(x|Ci), 由条件(iv)得fi(x)+xTwi 又因为函数G=(G1,…,Gk)R→Rk,每一个Gi:Ifi(x)→R,i=1,…,k是严格单调递增的可微实值函数,则有 Gi(fi(x)+xTwi) 由条件(i)结合上式可知 上式两边同乘以λi再求和得 (6) 因为设x是规划(MP)的任一可行解,(y,λ,β)是规划(DMP)的可行解,则 g(x,uj)g(y,uj),j∈△。 由于每一个Gi,j∈△是严格单调递增的可微实值函数,所以有 Gj(g(x,uj))Gj(g(y,uj)),j∈△。 结合条件(ii)知 εj0,j∈△, (7) 给(7)式两边同时乘以βj并且求和可得 (8) 将(6)式和(8)式相加结合条件(iii)整理得 (9) 由F的性质以及K-T条件知: 这与(9)式矛盾,故F(x)≮G(y)。 证明因为x是规划(MP)的一个有效解,并且在x处K-T条件满足,则 βjg(y,uj)0,j∈△, f(x) 也就是F(x) 定理4 (严格逆对偶)假设x0,(y,λ,β)分别是问题(MP)和问题(DMP)的可行解且f(x0)=f(y),如果满足下列条件: (i)fi在y处是广义对称G-(F,α,ε)-凸函数; (ii)g(x,uj)在y处是广义对称G-(F,α,ε)-拟凸函数; 则x0=y。 证明反证法。假设x0≠y,因为x0,(y,λ,β)分别是问题(MP)和问题(DMP)的可行解,所以 βjg(x0,uj)0βjg(y,uj),j∈△, 也就是 βjg(x0,uj)-βjg(y,uj)0,j∈△。 由于βj0,则g(x0,uj)g(y,uj),j∈△, 根据每一个Gi,j∈△是严格单调递增的可微实值函数,结合上式整理知 βj(Gj(g(x,uj))-Gj(g(y,uj)))0,j∈△。 又根据条件(ii)知 βjεj0, (10) 对(10)式两边求和得 又因为f(x0)=f(y), 而且根据条件(i)可知 上式两边同乘以λi再求和得 (11) 由(DMP)的约束条件可得 (12) 将(10)式和(11)式相加结合条件(iii)整理得 (13) 由F的性质以及K-T条件知 gs(x0,uj)), gs(x0,uj))≥0, 这与(13)式矛盾,故x0=y。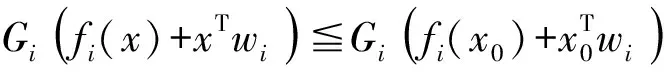
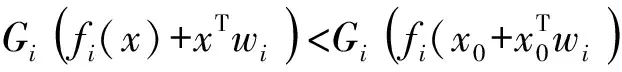
2 Mond-Weir对偶性条件