Riesz基的规范正交化及其性质
2022-01-11张建平
张 艳,张建平
(延安大学 数学与计算机科学学院,陕西 延安 716000)
框架与Riesz基的研究是小波分析理论研究的重要基础,站在空间元素表示这一层面,可以将框架看作是基组概念的延伸。Hilbert空间中的框架可以将空间H中的任意元素表示成∑cjφj的形式,但系数cj通常并不是唯一的,这是与正交基的区别之处,因此许多数学工作者根据实际应用,选择合适的系数对框架进行研究。框架、Riesz基与规范正交基之间既有密切联系又有本质区别。
文献[1]中给出Riesz基的等价条件:框架{φj|j∈J}是线性无关的;文献[2]中给出Riesz基与正交基之间的关系。本文主要是将Hilbert空间中Riesz基和Euclid空间中一组线性无关向量进行类比,将Riesz基进行规范正交化得到与之对应的规范正交基,这样就把一个下界为A上界为B的Riesz基转化为与之对应的规范正交基。另外讨论了Riesz基在标准正交基下的坐标以及同一Hilbert空间H中两组Riesz基之间的联系。
1 预备知识
本文中指标集J表示可数集或有限集,例如,自然数集N和整数集Z。
L2([a,b])表示[a,b]上的平方可积函数空间,其内积定义为

定义1[3-4]假设{φj|j∈J}是可分的Hilbert空间H中的一个函数序列,如果对于∀g∈H,存在常数A、B且0 则称{φj|j∈J}是Hilbert空间H中的一个框架,这里称A为框架的下界,B为框架的上界。特别的,如果A=B,则称框架{φj|∈J}为紧框架。 注:一般来讲,框架、紧框架都不是正交基,因为φj不是线性无关的。 框架与规范正交基有如下关系: 引理1[5]如果{φj|j∈J}是Hilbert空间H中的紧框架,框架界A=B=1且对所有的j∈J有||φj||=1,那么{φj|j∈J}构成一组规范正交基。 引理2[2]假设{φj|j∈J}是可分的Hilbert空间H中的一组向量,则下列命题等价: (1){φj∈J}是Hilbert空间H中的Riesz基; (2){φj|j∈J}是Hilbert空间H中的框架且{φj|j∈J}是线性无关的。 引理3[6]设S={en}是Hilbert空间H中的一个标准正交系,则以下条件等价: (1)S是H的标准正交基; 由(2)可以看出{〈x,ek〉}相当于Rn的直角坐标系,成为x关于标准正交基{en}的正交坐标。 定理1 如果函数族{φj(x)|j∈J}构成Hilbert空间H中下界为A上界为B的Riesz基,那么可以将{φj(x)|j∈J}进行规范正交化得到与之对应的一组规范正交基。 φ2(x)-〈φ2(x),e1(x)〉e1(x)≠0并且 〈φ2(x)-〈φ2(x),e1(x)〉e1(x),e1(x)〉= 〈φ2(x),e1(x)〉-〈φ2(x),e1(x)〉〈e1(x),e1(x)〉=0, 以此类推,假设en-1(x)已得,由于φn(x)与φ1(x),…,φn-1(x)均线性无关,显然φn(x)与 e1(x),…,en-1(x)线性无关,故 因此令en(x)= (1) 则有||en(x)||=1并且得en(x)⊥e1(x),en(x)⊥e2(x),…,en(x)⊥en-1(x),即{e1(x),…,en(x)}为Hilbert空间H中一组规范正交基。 平方可积函数空间是常见的Hilbert空间,下面用一个典型的实例验证方法的有效性。 例[7-8]若{1,x,x2,…,xn}是平方可积函数空间L2([-1,1])中下界为A上界B为的Riesz基,显然它不是标准正交基,故可用Schmidt正交化过程将其标准正交化为{en(x)},使得{en(x)}作为L2([-1,1])中的一个规范正交基。 解记φ1(x)=1,φ2(x)=x,因为 所以φ1(x)⊥φ2(x),因此可取 由(1)式得 一般地,可得 (2) 将En(x)代入(2)式,可以求得 从而可知{e1(x),e2(x),…,en(x)}是平方可积函数空间L2([-1,1])中的一组规范正交基。 由引理3,可得以下结论: 定理2 设{φ1(x),…,φn(x)}是Hilbert空间H中的一组Riesz基,{e1(x),…,en(x)}是H中的一组标准正交基,∀φj(x),φk(x)∈{φ1(x),…,φn(x)},他们关于基{e1(x),…,en(x)}的坐标分别是(〈φj(x),e1(x)〉,…,〈φj(x),en(x)〉),(〈φk(x),e1(x)〉,…,〈φk(x),en(x)〉)。那么φj(x)+φk(x)关于这个标准正交基的坐标为(〈φj(x)+φk(x),e1(x)〉,…,〈φj(x)+φk(x),en(x)〉);设a∈F, aφj(x)关于这个标准正交基的坐标为 (a〈φj(x),e1(x)〉,…,a〈φj(x),en(x)〉)。 证明设{φ1(x),φ2(x),…,φn(x)}是Hilbert空间H中的一组Riesz基,∀φj(x),φk(x)∈{φ1(x),…,φn(x)},他们关于基{e1(x),…,en(x)}的坐标分别是 (〈φj(x),e1(x)〉,…,〈φj(x),en(x)〉)和 (〈φk(x),e1(x)〉,…,〈φk(x),en(x)〉)。 φj(x)+φk(x)= 如果a是数域F中的一个常数,那么 对于Hilbert空间H中的两组Riesz基来说,在同一标准正交基下的坐标一般是不相同的,下面给出这两组Riesz基之间的关系。 定理3 如果{φ1(x),…,φn(x)}和{φ1(x),…,φn(x)}分别是Hilbert空间H中的两组Riesz基,{e1(x),…,en(x)}是H中的一组标准正交基,那么这两组Riesz基可以相互转换。 证明设函数族{φ1(x),…,φn(x)}和{φ1(x),…,φn(x)}分别是Hilbert空间H中的两组Riesz基,{e1(x),…,en(x)}是H中的一组标准正交基,则可表示为 从而就得到同一空间H中两组Riesz基之间的关系:2 Riesz基规范正交化过程
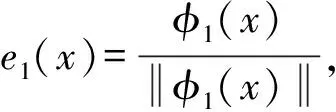




3 与Riesz基有关的两个结论





