Fang Yuan(袁方), Cheng-Jun Bai(柏承君), and Yu-Xia Li(李玉霞)

College of Electrical Engineering and Automation,Shandong University of Science and Technology,Qingdao 266590,China

Keywords: chaos,discrete memristor,cascade chaotic system,bifurcation

1. Introduction

Memristor, as the fourth basic circuit component, has some special characteristics,such as inherent nonlinearity and synaptic plasticity. According to the mathematical models,memristors can be classified into extended memristor,generic memristor, and ideal memristor.[1]Different memristors exhibit different properties. Since the unique characteristics of memristors, chaotic circuits,[2–4]neuromorphic computing systems[5–7]and other nonlinear systems[8,9]used to describe many problems in the fields of biology, physics, and economics can be easily constructed by combining memristors with other devices, which makes memristors be applied broadly in a potential application prospect.

Chaotic and hyperchaotic behaviors can be found in continuous and discrete nonlinear dynamical systems,[10–17]which have many unique behaviors, including topological transitivity, initial state sensitivity, and periodic orbit density.[18–21]In order to obtain new chaotic systems with rich repertoires of nonlinear behaviors,memristors were introduced into some classical chaotic circuits.[22–25]In addition,a cascade method of forming a series of new systems by cascading two chaotic subsystems was proposed in our previous papers.[26,27]Theoretical verification and experimental results manifested that the Lyapunov exponents and chaotic space of the new cascade chaotic system are much larger than those of subsystems.

As we all know, systems can be classified into continuous systems and discrete systems. Memristor is not an exception. Chua proposed that the concept of memristor can be extended to a much more general class of dynamical systems called memristive systems (or generalized memristors),and the memristor is only a special case of the systems.[28]Compared with CM-based systems, DM-based systems can be naturally realized by digital platforms such as FPGA(field programmable gate array), DSP (digital signal processing),and other microprocessor platforms. Besides, discrete systems can be utilized to appropriately describe many complex problems in the real world. Hence, the DM and DM-based systems may have many potential applications. Based on this idea,some DMs have been proposed in recent years.[29–31]For example, in Ref. [32], Heet al.investigated a DM model which are applied to the H´enon map. The bifurcation diagram and Lyapunov exponents were studied. The simulation results confirmed that the new DM-based map has more complexities than the original H´enon map. What is more, Baoet al.proposed a new discrete hyperchaotic map, which was from a sampling switch-based memristor-based circuit.[33]Inspired by this work, a general DM model and its mapping model were reported in Ref.[34]. Based on the DM mapping model, four different DM models and their maps were provided. The excellent performances indicated that two of the DM mappings can generate hyperchaos and show the memristor initial-boosted behaviors. In addition to the ideal DM model,a simple two-dimensional(2D)non-autonomous DMbased hyperchaotic map was proposed by Deng,which shows the bursting behaviors.[35]The above DM models and mappings all indicate that designing a chaotic discrete map with more complexities and better performances is still a valuable research topic.

Encouraged by the above examples, the main contents of this paper can be introduced as follows. The DM chaotic map (DMCM) is first used as a seed map to construct new cascade systems (CSs). To demonstrate the cascade method,the constructions and signal flow of new CSs are given to describe the processes. Through the cascade operation,new CSs own more system parameters and expanded chaos areas. Besides,the maximum Lyapunov exponent is multiplied with the cascade time increasing, which means better chaotic performances. Detailed dynamic comparisons are explored to illustrate the improvements of CSs.

The rest of this paper is organized as follows. In Section 2, a DM model and its chaotic map are proposed and the correspondingi–vcurves are given. In Section 3,the cascade DMCMs are established, and the dynamic comparisons between the seed map and CSs map are explored.In Section 4,the proposed chaotic systems are implemented. Finally, conclusions of the paper are summarized in Section 5.

2. The DM model and the seed chaotic map

2.1. The DM model

In terms of the definition of CM,[1]an ideal chargecontrolled memristor can be defined as

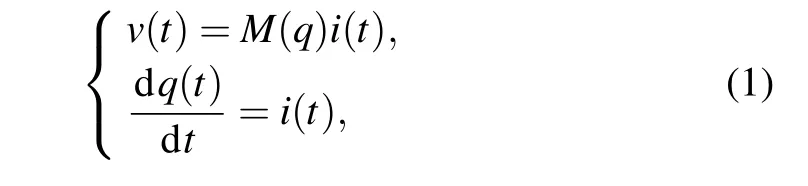
wherev(t) andi(t) represent the voltage and input current through the memristor, respectively.q(t) stands for a charge variable andM(q)is the memristance function.

According to Euler difference method,[33]the CM in Eq.(1)can be transformed into

wherevn,qn,andinrepresents the values of then-th iteration ofv(t),q(t),andi(t).

The equationqn+1=qn+kincan be deduced It can be found that the current state of the DM depends on all of the past states.

whereu,a,b,andkare system parameters.

Selecting parameters asa=1.5,b=−1,u=1.76, andk=1,different pinched hysteresis loops are given in Fig.1 by applying the discrete current sourcein=Imsin(ωn). For different amplitudesImand frequenciesω, the hysteresis loops are always pinched at the origin. The lobe area of the hysteresis loop decreases as the frequencyωincreases.These features are similar to those of CMs.

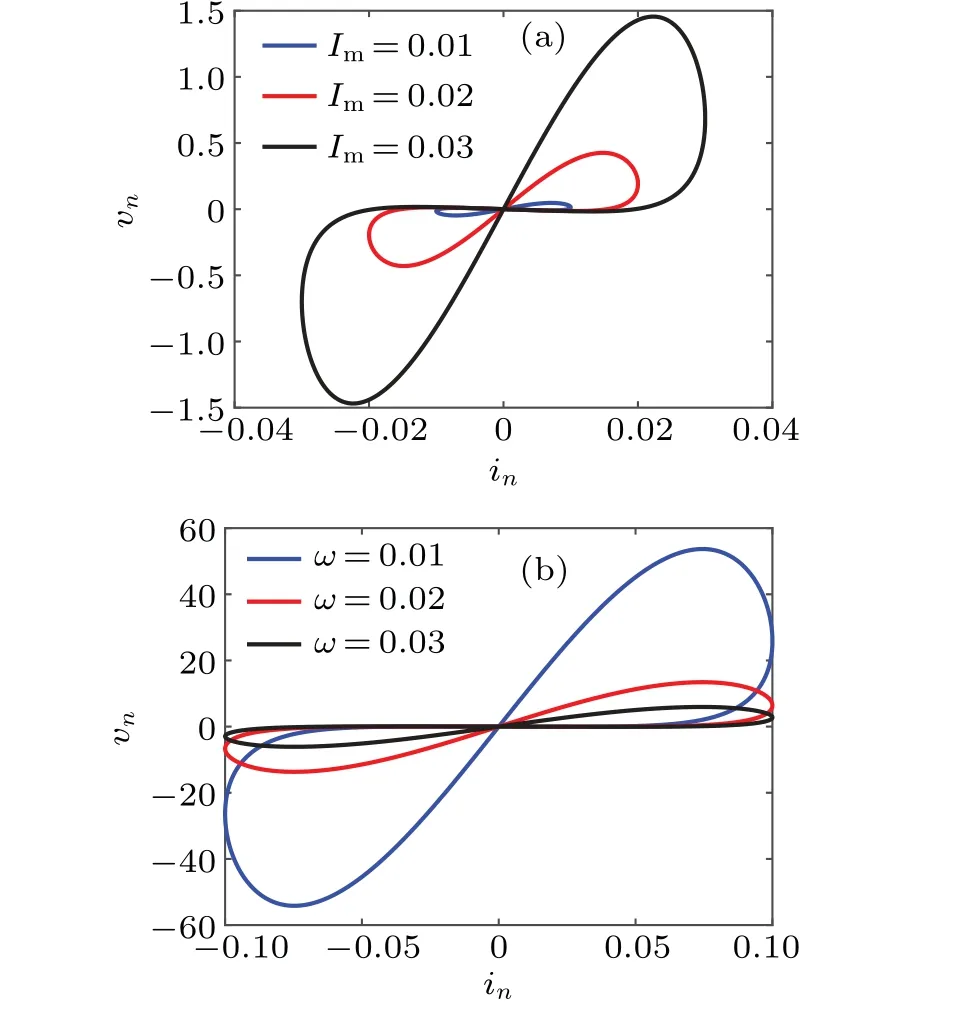
Fig. 1. The pinched hysteresis loops of the DM by applying (a) in =Im sin(0.01n) with Im = 0.01, 0.02 and 0.03; (b) in = 0.1sin(ωn) with ω =0.01,0.02,0.03.

2.2. The DM-based seed map

Based on the above-mentioned system(6),a DMCM was reported in Ref.[36],which can be constructed as follows:denoteinof the DM as the input for then-th iteration map andvnas the output and the next input of the iteration,then a twodimensional(2D)memristive map can be described as[36]

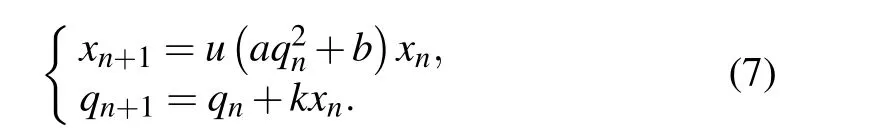
The corresponding schematic structure is plotted as Fig. 2,where we treat this 2D map asfx(xn,qn). This seed map was treated as a normal chaotic map. Then the signalqnis no longer regarded as the internal variable, but a signal that can be obtained as output. When the parameters are set asa=1.5,b=−1,k=1,andu=1.76 with initial value of(x(1),q(1))=(−0.1,0.1),the numerical simulations of DMCM are plotted in Fig.3. In this case,the Lyapunov exponents are calculated asLE1=0.2302 andLE2=0.0985. Thus,this map is hyperchaotic which will be used as a seed map for the cascade.

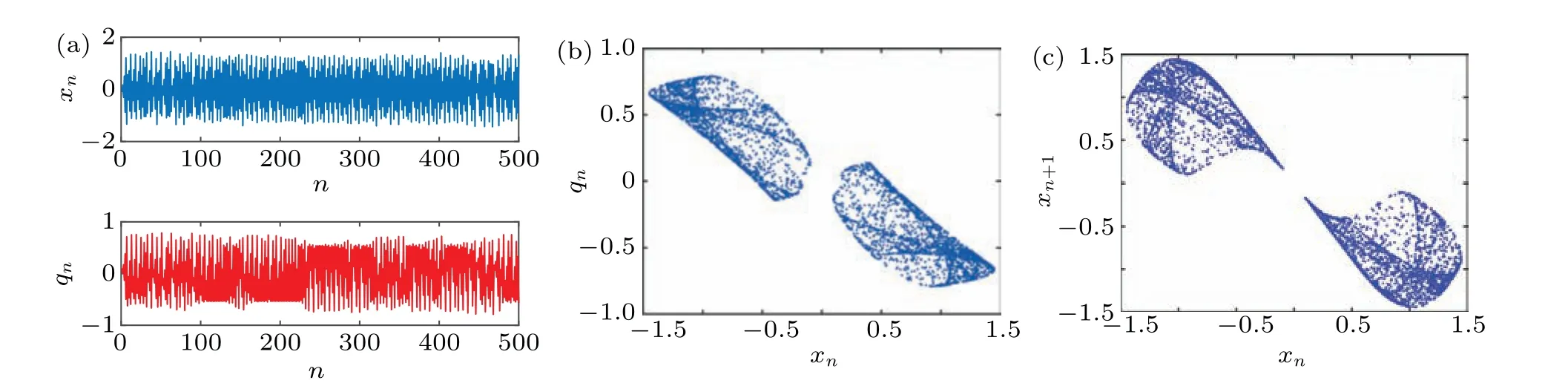
Fig.3. Numerical simulations of DMCM(7): (a)iterative sequences of xn,qn,(b)phase portrait of xn–qn,(c)attractor of fx.

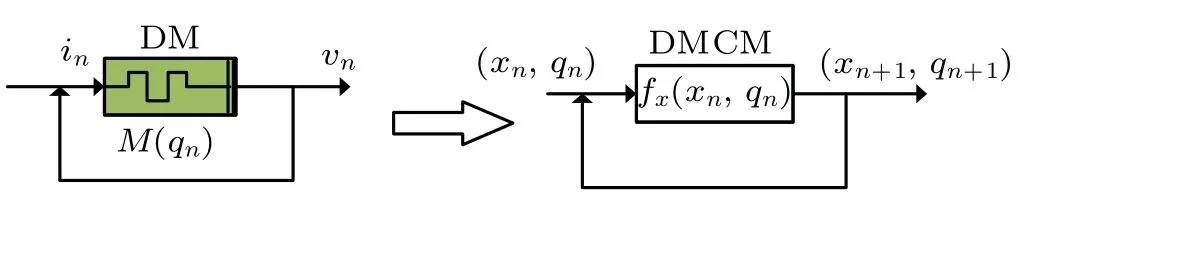
Fig.2. The schematic structure of DMCM.

3. The cascade DMCMs and dynamic comparisons

3.1. The cascade method of DMCMs

Motivated by the cascade structure in electronic circuits,the above-mentioned DMCM seed map can be utilized to cascade to construct more complex systems.Any number of DMCMs can be connected in series as shown in Fig.4 to construct a new CS.Each DMCM sends its output to the latter until the last DMCM feeds its output back to the first one. Some cascade examples are given below.

3.2. Cascade with two DMCMs

To demonstrate the proposed method,the simplest CS can be constructed from the seed map as shown in Fig.5(a),where two DMCMsfx(xn,qn)andfy(yn,q∗n)cascade with each other.The first seed map sends the outputs (xn+1,qn+1) to the second map as the input signal,while the second map feeds back its outputs (yn+1,q∗n+1) to the input of the first. The detailed signal flow diagram of CS is described as shown in Fig.5(b).

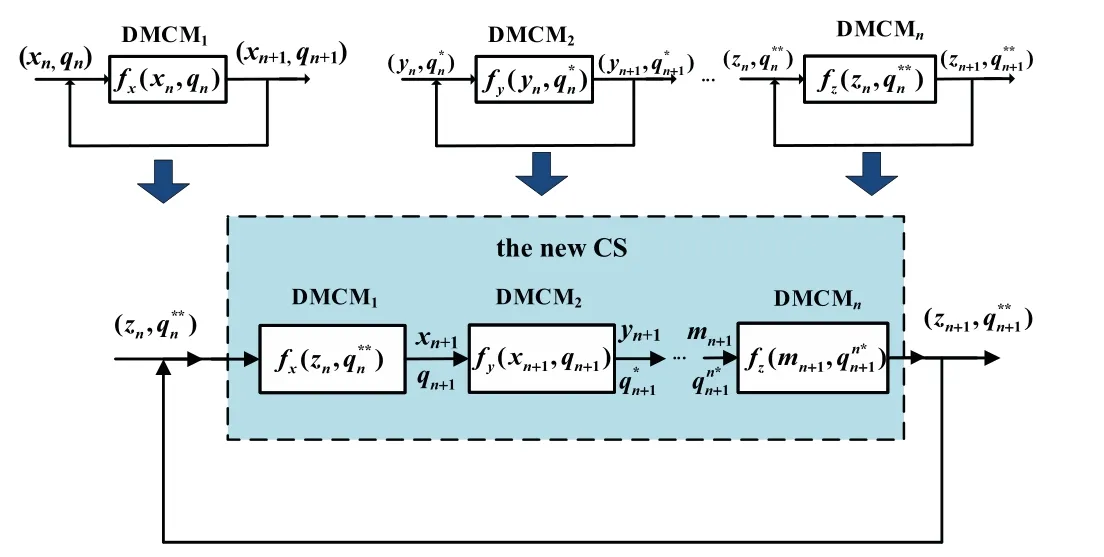
Fig.4. The structure of multi-DMCM cascade.

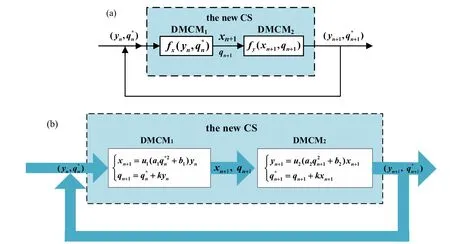
Fig.5. The cascade of two DMCMs: (a)the structure chart and(b)the inner signal flow diagram.

Fig.6. Numerical simulations of CS(8): (a)iterative sequences of yn,(b)phase portrait of yn–q∗n,(c)attractor of fy.

Obviously, the CS contains all parameters of its seed maps leading to a more complex structure. Setting parameters as the seed maps,there area1=a2=1.5,b1=b2=−1,k=1,andu1=u2=1.76. When the initial conditions are selected as(−0.1,0.1)and(0.1,0.1),the CS can generate chaotic oscillation and attractors as shown in Fig.6.

3.3. Cascade with three DMCMs

Fig.7. The cascade of three DMCMs: (a)the structure chart and(b)the inner signal flow diagram.

Similarly, a CS with three DMCMs can be constructed as shown in Fig. 7(a), in which the DMCMs are defined asfx(xn,qn),fy(yn,q∗n), andfz(zn,q∗∗n). The three DMCMs are connected in series. Each DMCM sends its output to the latter and the last DMCM feeds its output back to the first one.The corresponding internal signals of the CS are shown in Fig.7(b).

Then the CS can be obtained as

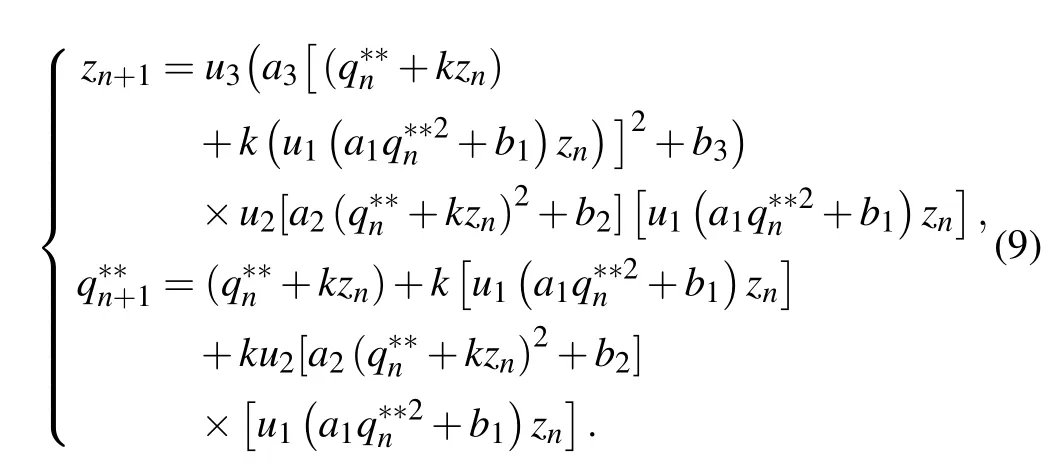
Setting parameters asa1=a2=a3=1.5,b1=b2=b3=−1,k=1,andu1=u2=u3=1.76,the new CS also keeps chaotic state as shown in Fig. 8. Although the chaotic iterative trajectories and phase diagramzn–q∗∗nare similarly with the seed map(Figs.3(a)and 3(b)),the system attractors are totally different,which means the change of the inner topology.

3.4. Dynamic comparisons

Chaos-cascade can significantly enlarge the maximum Lyapunov exponent and enhance the complexity of dynamic characteristics, which had been reported in previous researches.[26,27]In this case,since the seed DMCM is chaotic,their CSs also may have better dynamic features.

Takinga1=1.5,b1=−1, andk=1 in seed map (7),with initial value of(−0.1,0.1),the bifurcation diagram with respect tou1is shown in Fig.9(a). The chaotic region of the seed system is mainly distributed inu1∈(1.65,1.85). For CSs(8)and(9),since the cascade operation increases the system parameters, the two CSs have more bifurcation variables and parameter configurations. Let parameters be the set ofa1=a2=a3=1.5,b1=b2=b3=−1,andk=1. The corresponding bifurcation graphs ofu1,u2,andu3are displayed in Figs. 9(b)–9(f). Obviously, the more system parameters provide the possibility for flexible parameter configurations.With appropriate parameters, the CSs have the larger chaotic areas than the seed map. The more cascade times,the larger chaotic areas of the system.

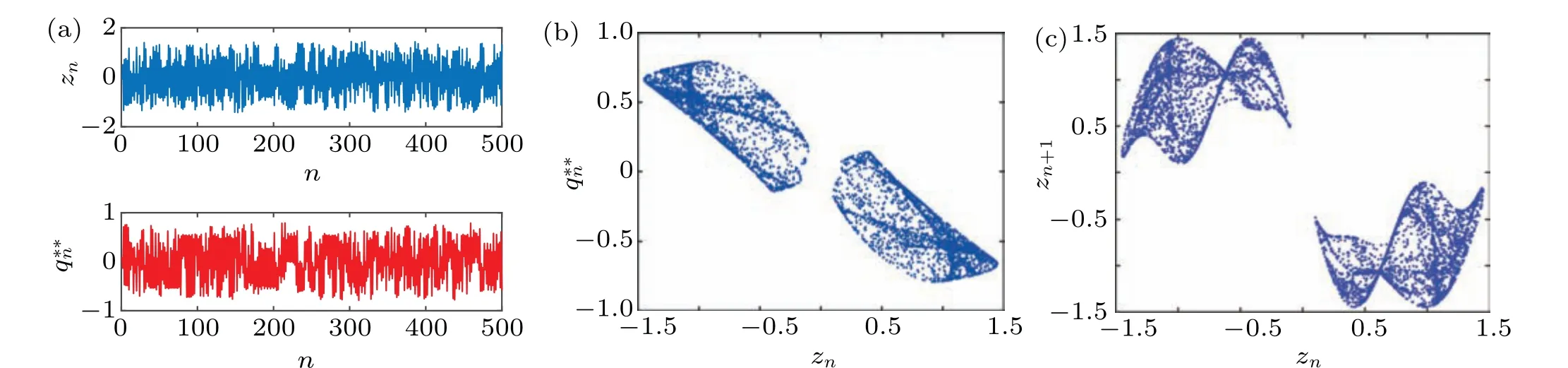
Fig.8. Numerical simulations of CS(9): (a)iterative sequences of zn and q∗∗n ,(b)phase portrait of zn–q∗∗n ,(c)attractor of fz.

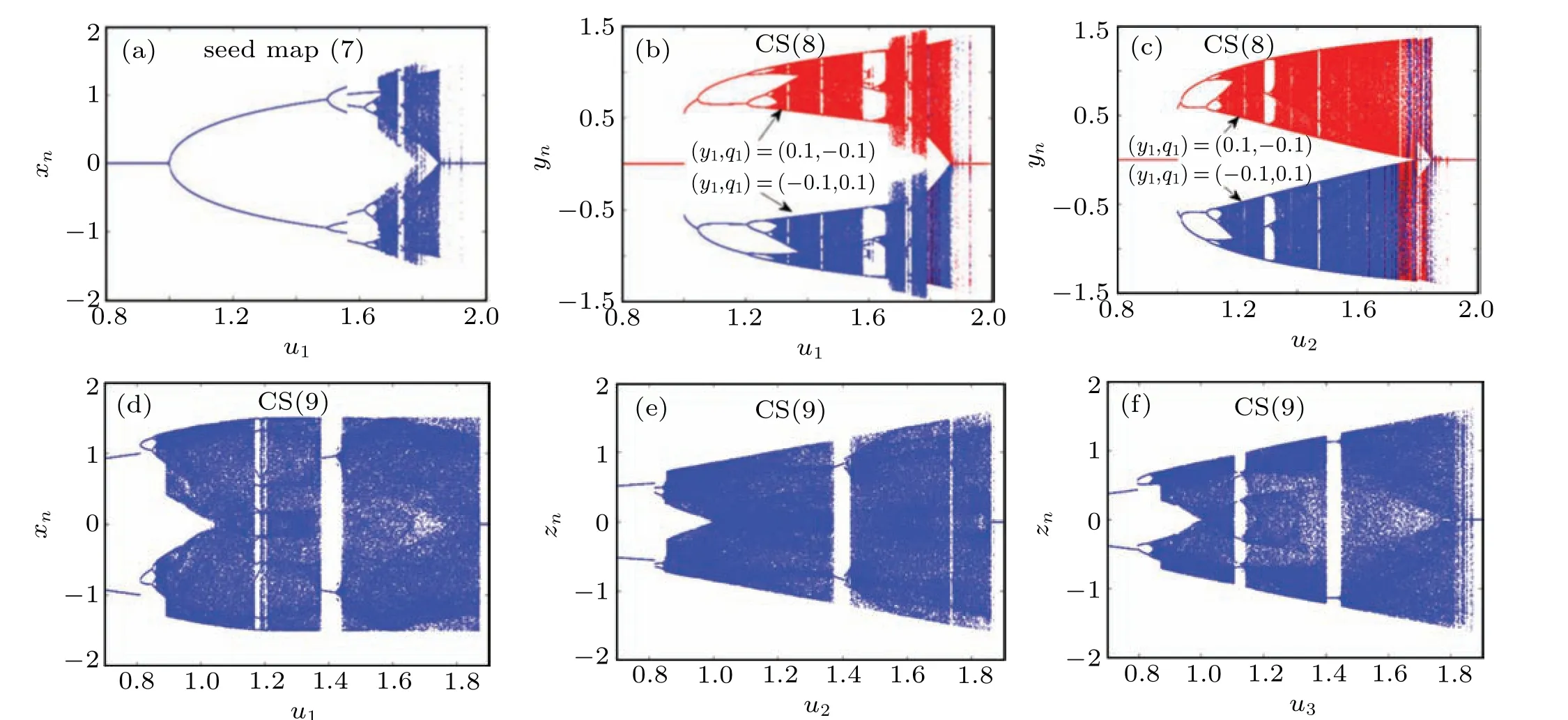
Fig.9. The bifurcation diagrams of(a)seed map(7),(b)CS(8)with u2=1.76,(c)CS(8)with u1=1.86,(d)CS(9)with u2=1.76 and u3=1.83,(e)CS(9)with u1=1.83 and u3=1.83,(f)CS(9)with u1=1.76 and u2=1.86.

As mentioned above, the more system parameters mean the more parameter configurations, which may increase the chaotic parameter space. The expanded chaotic areas can be indicated from the dynamic maps, as shown in Figs. 10(a)–10(c),where the system initial values are all set as(−0.1,0.1).In these dynamic maps, the states of systems can be divided into five situations as the parameters change, namely fixed point (yellow color), period (cyan color), chaos (blue color),hyperchaos (black color), and divergence (red color). From the bottom left corner of dynamic maps,the two CSs all start from fixed point to periodic state via bifurcation, and jump into chaotic or hyperchaotic state through period doubling bifurcation. Then the system orbits turn to periodic state again from the reverse period-doubling bifurcation route,and finally move infinity as the parameters increase. Some typical system orbits are described in Fig. 10(d) for clearly displaying the variation of system states.

Compared with CSs (8) and (9), the chaotic and hyperchaotic areas with respect tou1andu2obviously become larger as the time of cascade increases. Because of cascade effect,the new parameter configurationu1–u3emerges in CS(9).This new configuration brings new chaotic parameter space as shown in Fig.10(c). Thus,new CSs own better performances in terms of chaotic dynamics.

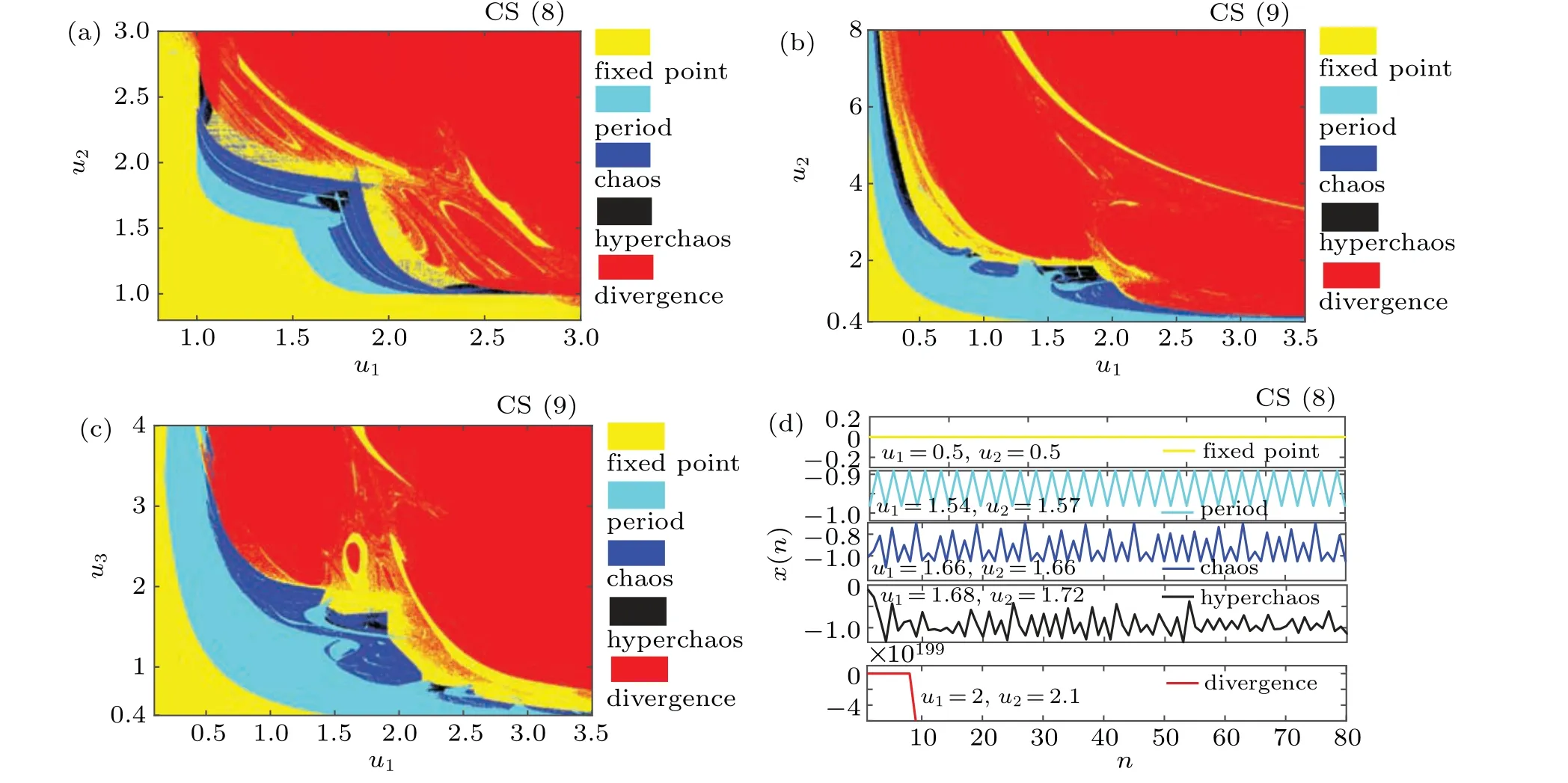
Fig.10. Dynamic maps with respect of(a)u1–u2 in CS(8),(b)u1–u2 in CS(9),(c)u1–u3 in CS(9),and the typical system orbits of(d)CS(8).

Except for the expanded chaos areas, the CSs also own larger Lyapunov exponents.As shown in Fig.11,the seed map owns the maximum Lyapunov exponent asLEmax=0.3244,while it increases toLEmax=0.6704 in CS (8) andLEmax=0.9667 in CS(9),respectively.The maximum Lyapunov exponent is multiplied compared with the seed map and increases with the cascade times. Since a larger Lyapunov exponent indicates more sensitive to changes of initial conditions,the CSs obviously own better statistical performance for the chaos generation.

Fig.11. The Lyapunov exponent spectra of the(a)seed map(7),(b)CS(8),(c)CS(9).

4. Hardware implementation

The proposed DM and its CSs are further implemented by digital signal processor(DSP)platform,where the core processing chip is TMS320C5509 and an 8-bit DA converter(TLC7528C)is used to convert numerical signals to analog voltage signals.

Fig.12. The pinched hysteresis loops obtained by DSP:(a)in=Im sin(0.01n)with Im=0.1,0.2,and 0.3;(b)in=0.1sin(ωn)with ω =0.01,0.02,and 0.03.

Fig.13. DM chaotic sequences implemented on DSP platform. (a)Hardware device,and chaotic sequences generated by(b)seed map(7),(c)CS(8),(d)CS(9).

For different values ofImandω, the corresponding pinched hysteresis loops of the DM are obtained by the oscilloscope BSO-X3034A as shown in Figs. 12(a) and 12(b),respectively. These experimental results are consistent with the numerical simulations in shown Fig.1.

Since the proposed DMCM and CSs are discrete systems,they can be naturally realized by digital platforms. Set parameters asa1=a2=a3=1.5,b1=b2=b3=−1,u1=u2=u3=1.76, andk=1. The seed map(7), CSs(8)and(9)can generate chaotic sequences in the range of(−1.6,1.6). These sequences need to be converted and scaled up to the range of(0, 255) to adapt the 8-bit DA converter. The final experimental device and results are displayed in Fig. 13. It can be concluded that the generated chaotic sequences prove the feasibility of hardware implementation of DM chaotic maps.

5. Conclusion

In this paper, motivated by the cascade structure in electronic circuits, a DMCM is used as a seed map to construct CSs. Any number of the seed map can be connected in series to design new CSs. Compared with the seed map, these new CSs have more parameters and extended chaotic parameter space. As the times of cascade increases, the maximum Lyapunov exponent of CSs also significantly increases. Finally,the proposed systems are implemented on DSP platform.The experimental results indicate these new CSs can be used to generate pseudo-random sequences and applied to encryption fields.