程时宇，黄志强，李冬梅

(桂林理工大学土木与建筑工程学院,广西 桂林 541004)

在超静定问题求解方法中,力法是重要的方法之一,也是其他超静定解法的基础。在结构力学的基本知识点中,对称性问题不但可以深化基本概念的理解,同时可分析结构的内力特征与变形特征。应用对称性内力特征与变形特征可简化结构体系,这为手算或定性分析超静定结构体系带来了极大的便利。同时,由于对称性所形成的内力特征与变形特征蕴含丰富的数学知识与力学知识,深入讨论其内在联系,可开阔在其中的“小天地”。在众多的教学教材描述中,对其中的内在描述未深入探究,教与学中也带来了盲点。

1 对称性结构在对称荷载下内力特征

从杨茀康[1]编写的教材可知,对称结构在对称荷载作用下,对称轴轴线处内力特征可依据力法方程:

δ11X1+δ12X2+δ13X3+Δ1P=0；δ21X1+δ22X2+δ23X3+Δ2P=0；δ31X1+δ32X2+δ33X3+Δ3P=0。

其中,X1，X3均为对称轴处正对称的多余未知力；X2为正称轴处反对称的多余未知力。

若荷载也关于对称轴对称,则自由项:

即正对称荷载作用下,力法的典型方程为:

δ11X1+δ13X3+Δ1P=0；

δ31X1+δ33X3+Δ3P=0。

由此得到正对称荷载作用下,对称轴处只存在正对称的内力。基于线性代数的理论,理解上述过程容易。然而反对称荷载作用在对称结构上,问题带来了一定的不确定性。

在反对称荷载作用下的弯矩图是反对称的。由图乘法及自由项的定义可知：

因此典型方程可化简为:

δ11X1+δ13X3=0;
δ22X2+Δ2P=0;
δ31X1+δ33X3=0。

很显然,此时未知力X2已与其他方程解耦,只需要分析δ11X1+δ13X3=0,δ31X1+δ33X3=0即可。

但从数学角度上无非直接得出X1=X3=0的结论,教材上普遍对于此结论做了简单说明,然而不经过严格证明无法使读者理解该结论的正确性。

2 线性代数分析齐次线性方程组

结合线性代数[3]的理论知识可知:

δ11X1+δ13X3=0；

δ31X1+δ33X3=0。

属于齐次线性方程组,齐次线性方程组有两种解答,一是只有零解,二是有无穷多组解(包含零解);齐次线性方程组只有零解的条件是系数行列式不为零;齐次线性方程组有非零解的条件是系数行列式为零,实质上系数行列式为零,即方程组间系数对应成比例,这相当于方程组中方程的数目小于未知数的数目,因此它有无数组解[4]。

由柔度系数形成的过程可知:

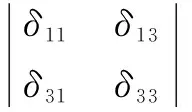
显然,若对一般的弯矩方程函数而言,上式绝对有机会为零,那么就不能得到X1=X3=0的结论。因此为了进一步研究分析,首先讨论直杆,由于单位荷载作用下的内力图均是直线,不妨假设:

所以：

显然,若a=b=c=d时,该系数行列式是为零的,即使c=d=0时,亦满足行列式为零,因此简单满足单位荷载下的弯矩图,仍然无法得到X1=X3=0的结论,因此通过上述解析解答,还无法得到结论,仅凭数学推导仍然解决不了问题。

3 结合力学特征求证在反对称荷载下内力特征

此时,对于反对称荷载作用下,可得出:X1=X3=0。

为了验证该结论的一般性,将对称结构中的构件分成两大类:一类与对称轴垂直相交的构件;一类与对称轴不相交(或斜交)的构件。如图1所示的水平杆件为与对称相交的构件,竖向构件为与对称不相交的构件。

由前述,多余未知力取为对称轴处的截面内力。而正对称的内力为轴力X1与X3,产生弯矩图时在两类构件中是不一样的。在与对称轴相交的构件中,由于X1为该构件的轴力,不产生弯矩,而X3产生的弯矩无论在哪类构件中均表现出弯矩均布。因此可得出如下系数关系:

1)与对称轴相交的构件:

此时图乘的结果满足:δ11δ33-δ31δ13=0。

2)与对称轴不相交(或斜交)的构件:

显然,若结构同时具有与上述两类构件,则算式可写成:

显然,对于上式而言恒为负值,即不会发生正负相加为零的结果,于是满足δ11δ33-δ31δ13≠0,因此可严谨得出X1=X3=0的结论。

然而,有些结构是只存在与对称相交的构件，如图2，图3所示。

对于图2,它的多余未知力如图4所示。

由于X1不产生弯矩,因此,δ11=0,δ13=δ31=0。在反对称荷载作用,典型方程简化结果表达式:

δ11X1+δ13X3=0;

δ31X1+δ33X3=0。

可得到X3=0,即对称轴处无弯矩内力的结论。然而X1轴力可为任意值,均可满足上述数学表达式。但在实际力学状态中,X1是由轴向拉压变形而产生的内力分量,而两端为固定端时,在小变形状态下,轴向是无伸缩量的,因此可进一步由物理力学概念确定X1=0。

对于图3所讨论杆轴线为曲线的情况,显然,该曲杆中,M1=1×(R-Rcosφ),M3=1。

δ11δ33-δ31δ13≠0。

因此对于曲杆而言,可由齐次方程组得到X1=X3=0的结论。

4 结语

由齐次方程组得到X1=X3=0的结论并非由于纯数学解答,基于对称结构在反对称荷载作用下,受力有明显特征,正是基于这种特征,使得内力图具有特定性,也因此,此时系数行列式不等于零。所以,通过力学问题转化为数学问题,再进一步结合力学特征才能完整解释在对称轴处不存在对称性内力的问题。