伍慧玲

( 闽江学院 数学与数据科学学院, 福州 350108 )

0 引言

本文考虑如下Choquard类型方程：

(1)

Choquard类型方程有着重要的物理背景,如Pekar用方程

(2)

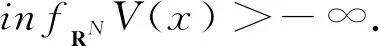
(V2) 对任意的a>0, meas({x∈RN:V(x)≤a})<∞, 其中meas(·)表示RN上的Lebesgue测度.

(F1)f∈C(RN +1,R), 且对任意的(x,s)∈RN×R,f(x,-s)=-f(x,s).

(F3)f(x,s)在R上关于s单调不减.

根据上述假设可得到如下定理:

定理1假设(V1)—(V2)和(F1)—(F3)成立,则方程(1)存在无穷多解.

(3)

1 记号及引理

(4)

因此,当η=1时泛函Eη(u)的临界点等价于系统(1)的解.

引理2[13]假设(V2)成立,则当2≤p<2*时,H⊂Lp(RN)是紧嵌入.

引理3若(F1)和(F3)成立,则对任意的u∈H{0},t≥0, 有

(5)

证明以下采用文献[9]中引理2.2的方法证明引理3.首先证明∀x∈RN,s1,s2∈R,t≥0,

ψ(x,s1,s2,t)=F(x,ts1)F(x,ts2)-F(x,s1)F(x,s2)+

(6)

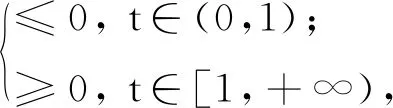
由式(4)可得

(7)

令g(t)=2tq-2+q-qt2, 于是有g′(t)=2qt(tq -2-1).显然g′(t)≤0,∀t∈[0,1];g′(t)>0,∀t∈(1,+∞).于是可得

g(t)=2tq-2+q-qt2≥g(1)=0.

(8)

(9)

由式(7)—(9)可得式(5)成立.证毕.

定理2(喷泉定理) 假设泛函Eη满足以下条件:

1) ∀(η,u)∈[1,2]×H,Eη(-u)=Eη(u),Eη将H中的有界集映射到R中的有界集;

3) 存在Rk>rk>0, 使得对所有的η∈[1,2],

2 定理1的证明

引理4若(V1)—(V2)和(F1)—(F2)成立,则存在序列{rk}使得当k→∞时,rk→∞且

证明由引理2和文献[15]中的引理3.8可得,当2≤l<2*时,有

(10)

再由式(4)和式(10)可得,∀u∈Zk,

(11)

引理5若(V1)—(V2)和(F1)—(F3)成立,则对于引理4中的{rk}，存在Rk>rk使得

(12)

(13)

下面先证明

(14)

(15)

由式(15)、条件(F2)、引理1和 Lebesgue 控制收敛定理可得,当n→∞时有

(16)

(17)

(18)

由条件(F3)可得f(x,u)u-F(x,u)>0, 进而有

(19)

(20)

由式(17)、式(20)和引理3可得