周婉娜，熊志平

（五邑大学 数学与计算科学学院，广东 江门 529020）

1 引言及预备知识

矩阵乘积广义逆的反序律和正序律在统计学、微分方程、电网络分析等领域都有着不可或缺的重要作用[1-2].20世纪60年代以来，很多学者研究了矩阵乘积广义逆的反序律，例如矩阵乘积的｛1｝-逆、｛1,3｝-逆、｛1,2,3｝-逆、M-P逆的反序律成立的充要条件，得到了很多有趣的结果和一些重要的应用算法[2-3].关于矩阵乘积广义逆的正序律的理论与应用研究相对较少，很多相关问题还需要进一步的解决，因此矩阵乘积广义逆的正序律成为了一个热点研究课题.

在本文中，Cm×n表示复数域中所有m×n矩阵，Im为m阶单位矩阵，0m×n为m×n零矩阵（常用0代表合适的零矩阵）.对任意的A∈Cm×n，A*为A的共轭转置，r（A）为A的秩，R(A)为A的值域，N(A)为A的零空间，相关概念参见文献[1,3].

定义 1[4]设A∈Cm×n，满足下列 4个 Penrose条件：1）AXA=A，2）XAX=X，3）（AX）*=AX，（XA）*=XA的矩阵X∈Cn×m称为A的M-P逆，记X=A+.

引理1[1]矩阵的M-P逆满足以下性质：A*(AA*)+=(A*A)+A*=A*(A*AA*)+A*=A+.

引理2[5]设矩阵A、B、C和D满足以下条件：R(B)⊆R(A)，R(C*)⊆R(A*)或R(C)⊆R(D)，R(B*)⊆R(D*)，则

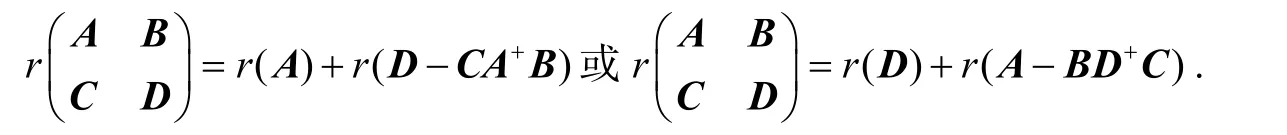
引理 3[6]设再设

则对于某些Xi有：

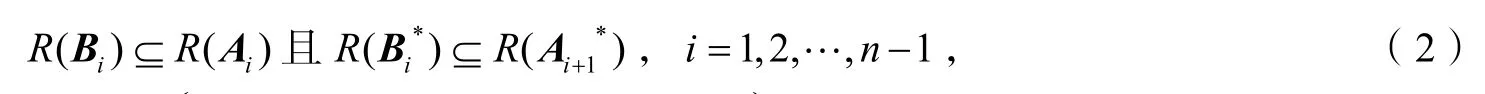
而且n×n分块矩阵的 M-P逆可以表示为：其中，

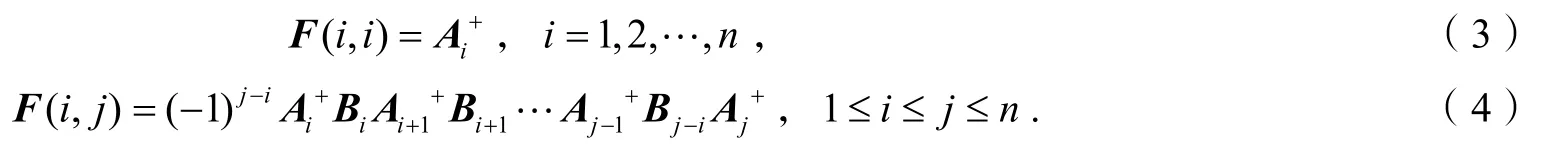
2 主要结果

定理1设则5×5分块矩阵的M-P逆可以表示为：

其中，M（i,j）可根据引理3中的式（3）和（4）给出，特别地，

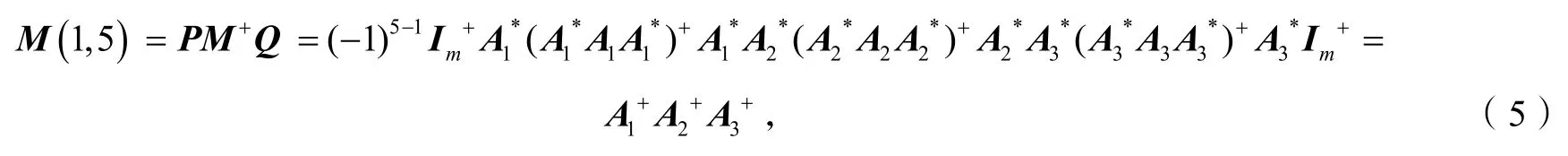
证明因为所以

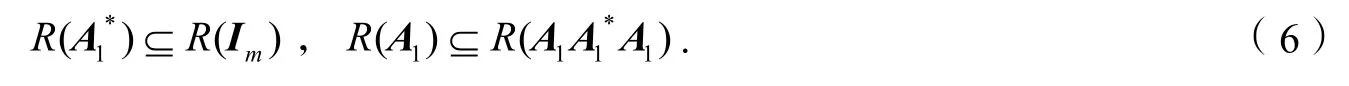
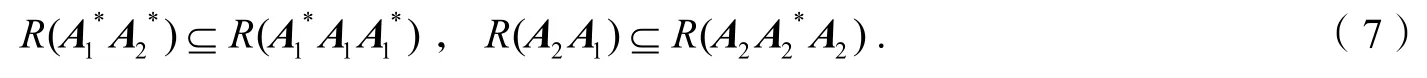
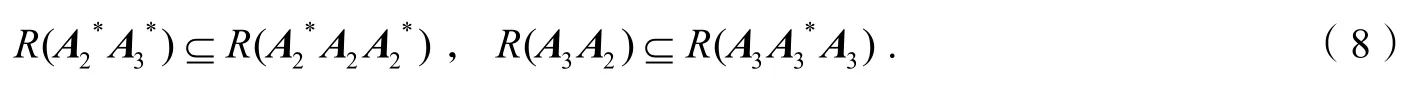
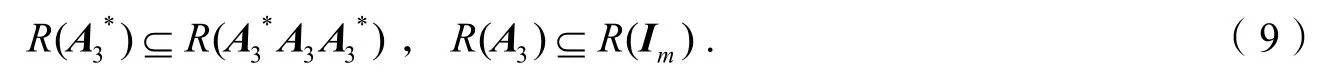
结合式（6-9）以及引理 3中的式（1-2），可以得出定理1的结论.特别地，根据引理 1，我们知道A*(A*AA*)+A*=A+.因此，可得：

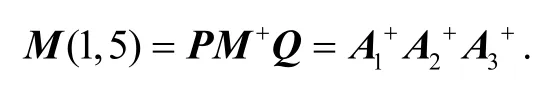
为了得到定理2，我们首先证明以下秩等式：对于任意的矩阵iA来说，

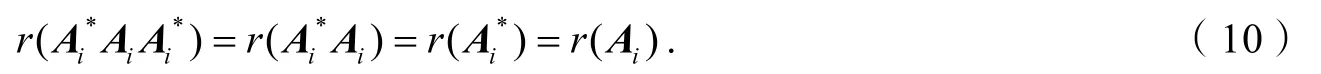
证明因为所以

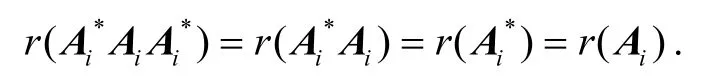
定理2设A1,A2,A3∈Cm×m且A=A1A2A3，M,P和Q由定理1给出，则：

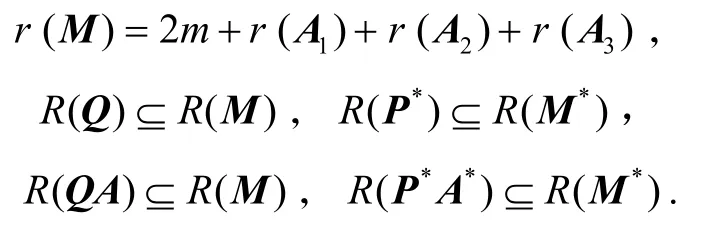
证明构造可逆矩阵D1,D2,D3,D4和列矩阵D5如下：

则

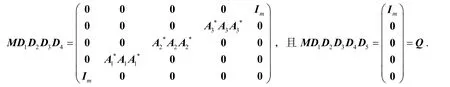
因此r(M)=r(MD1D2D3D4)=2m+r(A1)+r(A2)+r(A3)，且R(QA)⊆R(Q)=R(MD1D2D3D4D5)⊆R(M).

另一方面，构造可逆矩阵T1,T2,T3,T4和行矩阵T5如下：

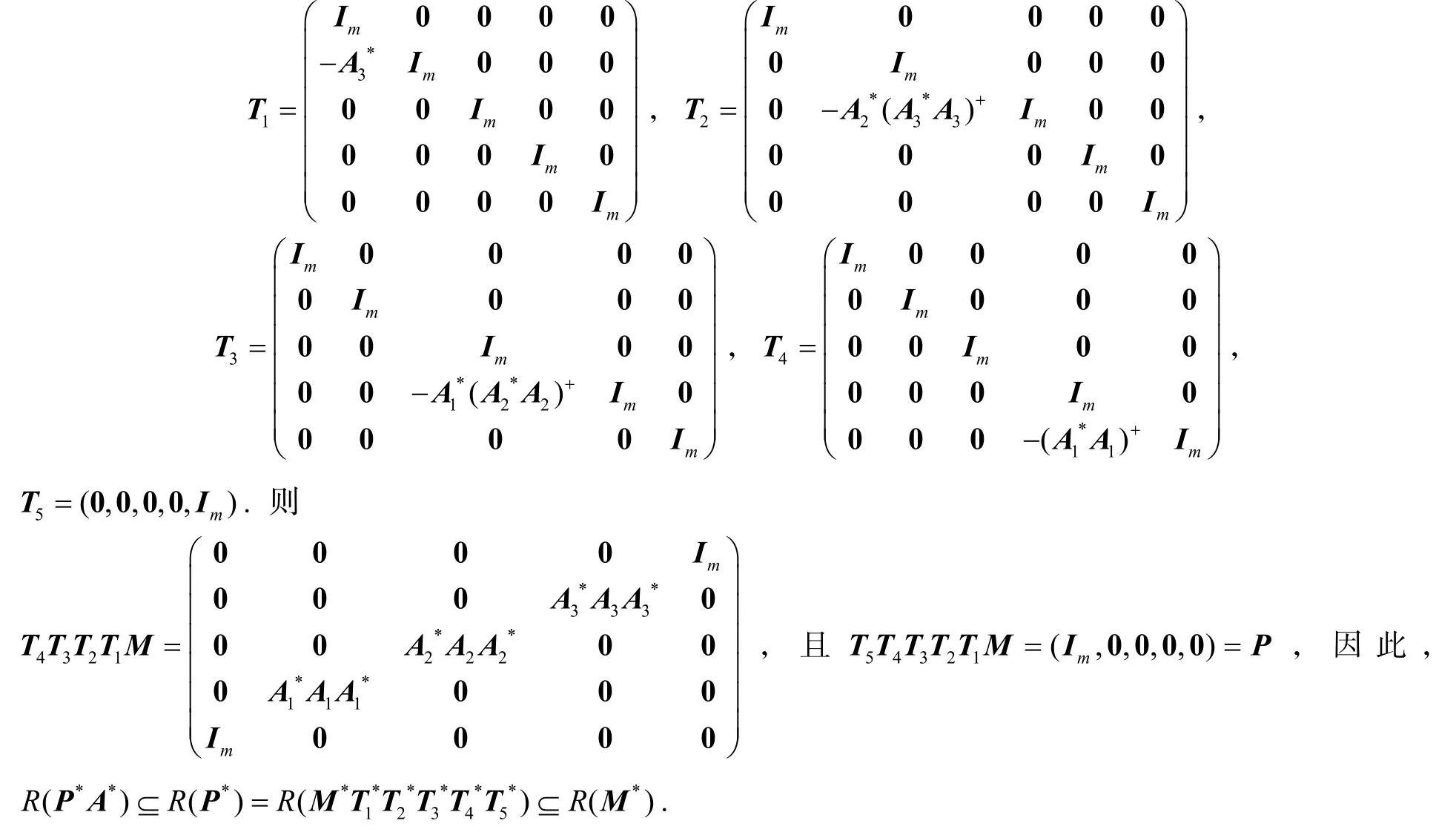
利用定理1和定理2可以得到定理3.

定理 3设且M,P和Q由定理 1给出，则以下等式等价：

其中，E1=（0,0,0,Im），E2=（0,0,0,Im）*，以及

证明由定理1可得成立的充要条件为

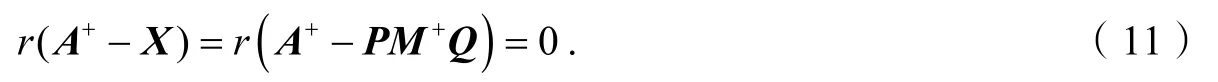
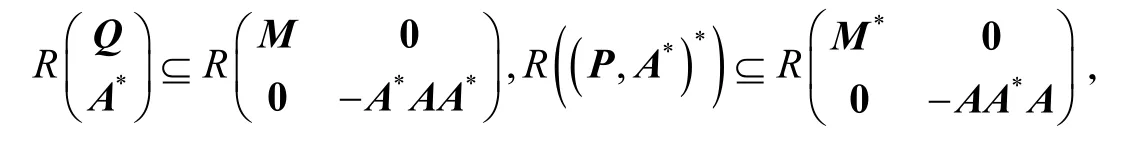
则

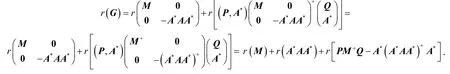
根据引理2、定理2以及式（10），可得：

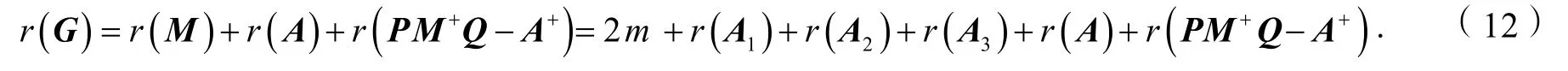
另一方面，

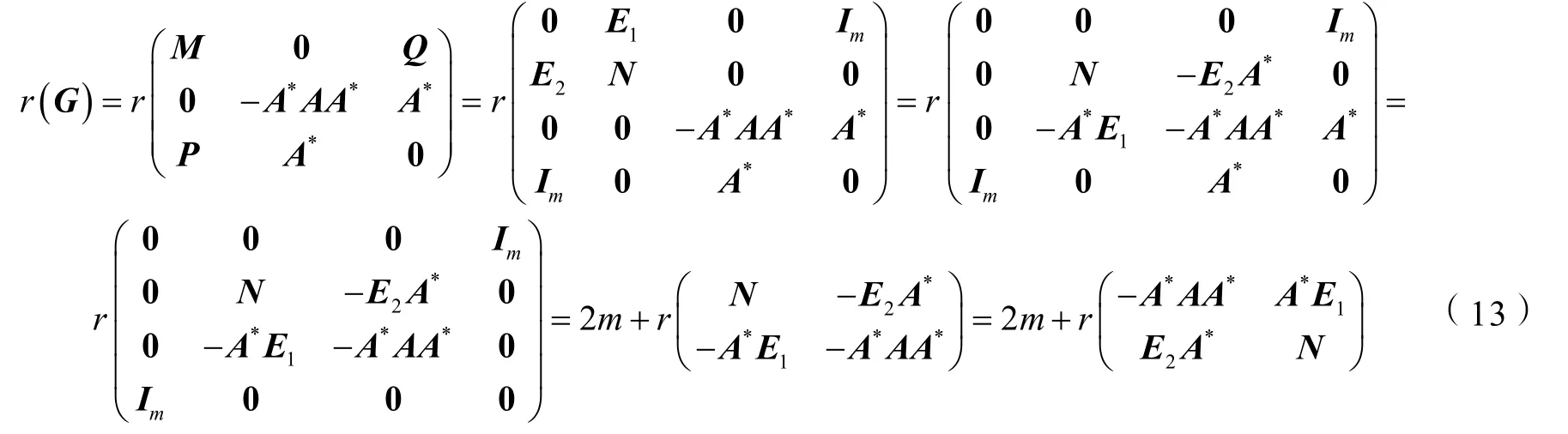
结合式（11-13）可知，定理3成立.

3 结论

对任意的矩阵Ai∈Cm×m,i=1,2,3，本文利用秩等式和广义 Schur补的性质，得出了 3个矩阵乘积的M-P逆正序律成立的充要条件.