李晓霞,王雪,冯志新,张启宇

(1河北工业大学省部共建电工装备可靠性与智能化国家重点实验室,天津 300130;2河北工业大学河北省电磁场与电器可靠性重点实验室,天津 300130)

0 引言

1971年,Chua[1]预测了一种本质为非线性电阻,且其电阻值可以通过流经的磁通或电荷的变化而发生变化的元器件,且定名为忆阻器。忆阻器是表征磁通量与电荷的元器件[2,3],其非线性[4]使它可以代替众多电路器件来构造非线性函数,且忆阻器的伏安特性曲线具有倾斜“8”字型的紧捏滞回线特性,在电路中易于引起振荡与混沌,这十分有利于混沌电路的搭建与实际应用,科研人员基于这一点构建了非线性电路。特别地,在基于忆阻器的混沌电路[5,6]与基于忆阻器的神经突触电路[7,8]方面取得了很大进展。

混沌现象已经被广泛研究了几十年,其中在混沌化[9]、混沌的控制[10−12]、混沌的同步与应用等方面[13−16]有很多重要的研究成果。混沌化指的是产生或者增强系统的混沌性这一过程,混沌化的增强可以提高网络的复杂性与难预测性,符合保密通讯领域对系统安全性的要求。一般来说,用三阶或者高阶的非线性常微分方程可以实现连续系统的混沌。除了常见的Lorenz系统[17−20],Sprott创造的19种含有非线性二次项的网络[21,22]也逐渐成为研究热点。这一系列Sprott系统的不同之处在于,包含常数项及多个非线性项在内的一系列微分方程组增加了系统的复杂性,满足科研过程中对于多种难以预测的混沌状态的需求。近年来对于该系统的研究大多针对其应用,如同步控制等[23,24]。对于Sprott系统本身混沌化增强的研究很少,并且鲜有对含常数的系统进行的电路实现分析。本文基于Sprott-B系统进行了包括混沌性验证、系统特性研究、动力学分析及电路实现在内的一系列研究。

当前应用于混沌电路系统中的忆阻器引进方法包括以下几种:1)基于现有经典系统,利用忆阻作为某一或多维的反馈项或直接增加一维忆阻变量来增强忆阻混沌特性[25−27];2)在混沌电路中选择一个非线性元件,然后用忆阻器将其替换[28,29]。

本文利用第一种忆阻器引进方法,基于Sprott-B系统,通过增加一个磁控忆阻器反馈量和一维忆阻变量,构建了一个新型超混沌四阶系统,并观察到了超混沌现象,与原Sprott-B系统相比,大大增强了混沌复杂特性及信号产生的随机性。然后进行了新型系统的特性分析,包括Lyapunov指数和维数、耗散性、无限多平衡点集与稳定性。接着分析了超混沌系统的动力学特性,其中通过分析随参数变化的分岔图,清楚地看到了通向混沌的过程,并观察到了瞬态混沌现象;通过对比随初始值变化的分岔图与Lyapunov指数谱,观察到多吸引子共存现象。最后,通过系统方程设计出相应电子模拟电路,实验相图与数值仿真结果一致,表明本系统可以应用于实际生产生活中。据了解,尚无文献讨论有关含常数项混沌系统的瞬态混沌与多吸引子共存等情况,本文创新性地构建了包含常数项的忆阻混沌系统,为高性能多复杂性的通讯保密网络奠定了基础。

1 基于忆阻器的Sprott-B超混沌忆阻系统

1.1 Sprott-B简单系统模型

简单Sprott-B模型可表示为

式中:状态变量为x=(x1,x2,x3)T∈R3,系统参数a=1,b=2,c=5,且当x1、x2、x3的初始值分别选取为(1,1,1)时,方程组(1)得到一个如图1所示的吸引子,经计算,系统(1)的Lyapunov指数为0.4753,0.0004,−2.4757。

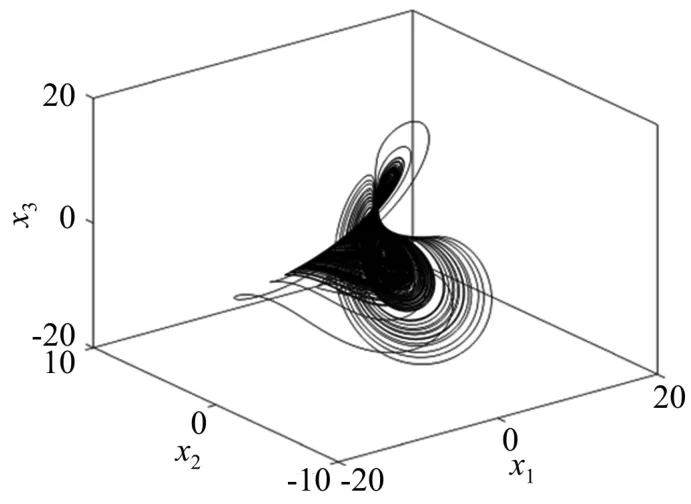
图1 Sprott-B系统的吸引子Fig.1 Chaotic attractor of Sprott-B system

1.2 超混沌忆阻系统模型

在系统(1)的基础上,分别在第二项上增加了一个忆阻反馈项,第三项增加了一个忆阻变量,并增加了一个第四项,得到了四阶忆阻系统

式中:k是表征与忆阻器有关的系数;W(x4)=−d+e|x4|是系统引入的忆阻性质的函数方程,此处选用磁控二次型忆阻器[30],且定义参数d=3,e=0.1。需要注意的是W(x4)虽与前述中忆导相同,但却是无量纲的。由忆阻器相关定义可知,磁控性忆阻器两端电流电压关系可表示为i=W(φ)v,˙φ=v,其中W(φ)表示由磁通量控制的方程,代表忆导值;φ代表磁通量。这里定义流经忆阻器的电荷为q,那么磁控二次型忆阻器的模型可表示为

式中a、b均为正常数,(3)式两端对时间t进行微分可得

式中W(φ)是二次型磁控忆阻器的忆导,dq/dt=i(t),dφ/dt=v(t),即得到

对于忆阻型电路来说,其动力学输出必定依赖于记忆变量的初始值,此处为磁通,对于不同的记忆变量初始值,会导致混沌系统在混沌与周期态之间相互的转化。当给定磁通初值φ0=0,施加电压v=sin(πt)时,得到如图2所示忆阻器的伏安特性曲线。由图2可知,引入增量确为忆阻性质的量,并且由捏滞回线落于伏安平面的第二和第四象限可知,v(t)i(t)<0,此处引入的是一个类似能量源的有源忆阻器。

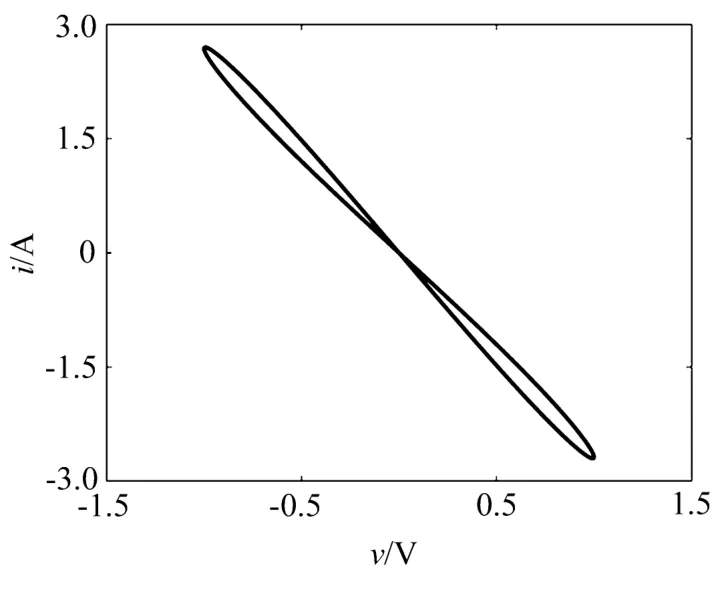
图2 忆阻器的伏安特性曲线Fig.2 Voltage-ampere characteristic of the memristor

选取参数a=3,b=15,c=30,k=1,初始条件(33,15,14,12),系统(2)产生的吸引子相图如图3所示。由吸引子图像观察得出本系统为超混沌状态系统,下面进行系统混沌性验证。

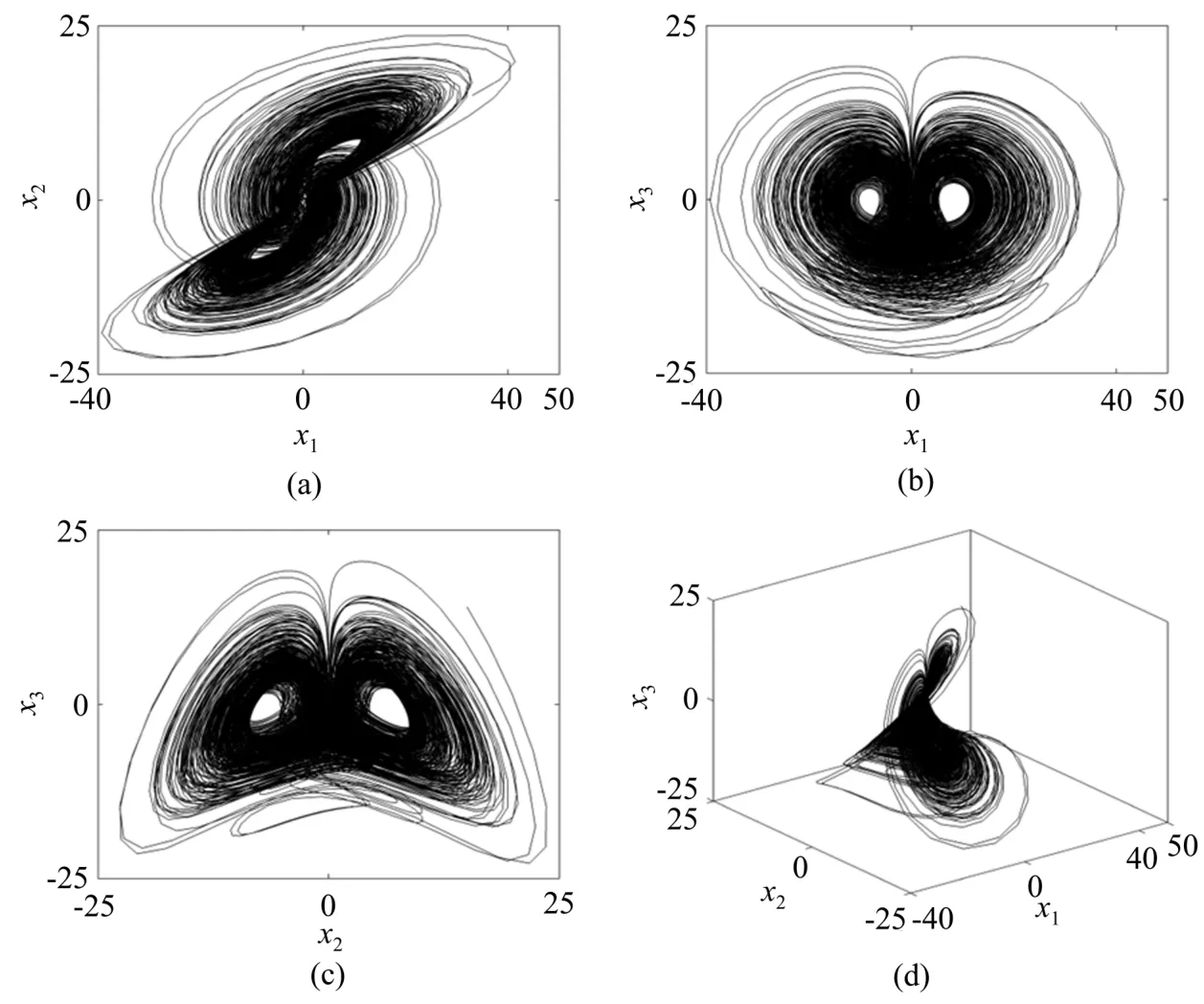
图3 系统(2)的吸引子。(a)x1-x2平面;(b)x1-x3平面;(c)x2-x3平面;(d)三维图Fig.3 Chaotic attractor of the system(2).(a)x1-x2plane;(b)x1-x3plane;(c)x2-x3plane;(d)Three-dimensional graphic

1.3 系统特性分析

1.3.1 Lyapunov指数和维数

正的Lyapunov指数是造成系统轨线以指数倍进行分离的根本原因。对于四阶超混沌系统,必有2个正的Lyapunov指数。经计算,系统(2)的4个Lyapunov指数LE1、LE2、LE3、LE4分别为3.0785、0.0132、−0.0253、−18.0664。最大的Lyapunov指数LE1远大于系统(1)的最大Lyapunov指数。说明本系统混沌特性大大增强。

根据Yorke公式[31]可求出Lyapunov维数,即

根据计算得出系统(2)的Lyapunov维数是3.1697,分数维的出现不仅代表本系统具有复杂的分形结构,还表示该系统会使附近的轨道产生分岔现象,也说明混沌现象确存在于本动力系统中。

1.3.2 耗散性

对于系统(2),有

说明系统具有耗散性,且以指数形式收敛,可表示为

即体积元在t时收缩至体积元V0e−15t,当t→∞时,含有轨迹的每一个体积元都将以指数率−15收缩至0,故本系统的所有运动都将固定至一个吸引子上。

1.3.3 Poincare截面与功率谱分析

Poincare截面分析是指在多维空间内选取一个截面,当Poincare截面上的图形是一定范围内的连续曲线或成片密集点的时候,运动状态为混沌。在系统(2)中,分别截取了x1=0与x2=1时的Poincare截面,如图4所示。观察到两个截面均为成片的密集点,故可判定系统(2)为混沌状态。

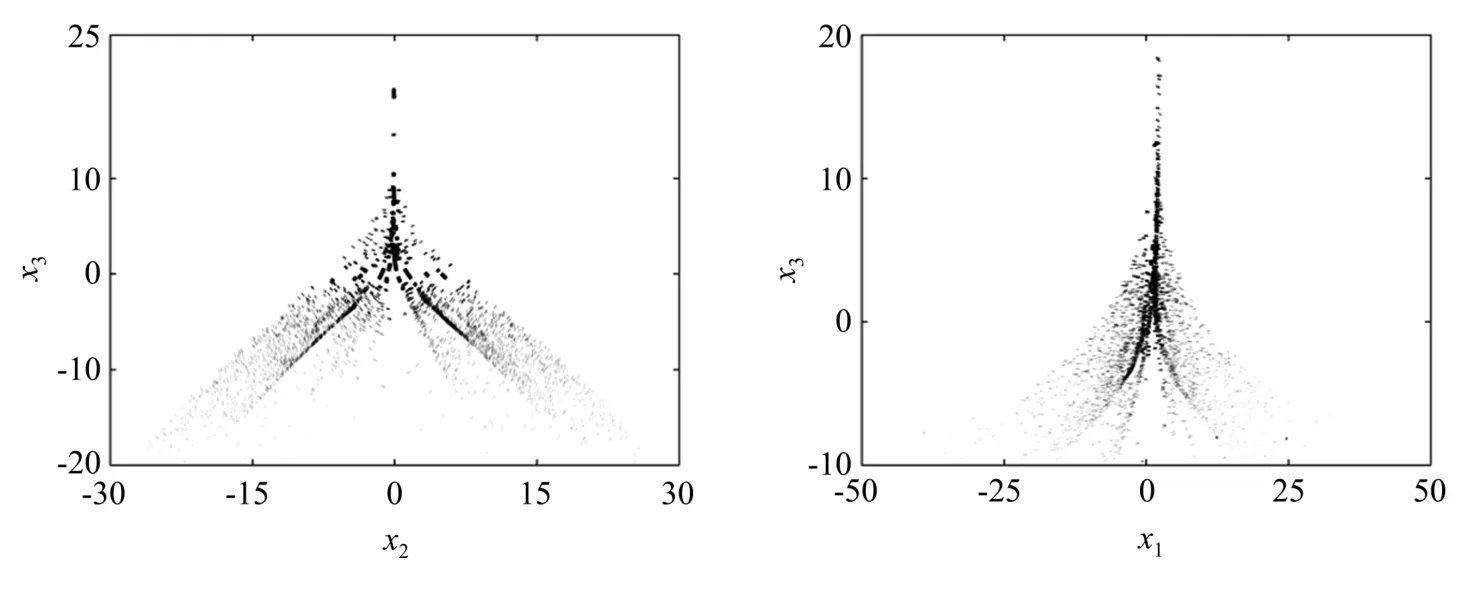
图4 Poinacer截面。(a)x1=0;(b)x2=1Fig.4 Poincare section.(a)x1=0;(b)x2=1

混沌运动的内在周期性导致其功率谱是连续的,呈现宽峰状态,没有明显波峰,并呈现类噪声和冲击式特点。系统(2)的功率谱如图5所示,由图可见系统(2)符合这些特点,说明新系统是一个混沌系统。

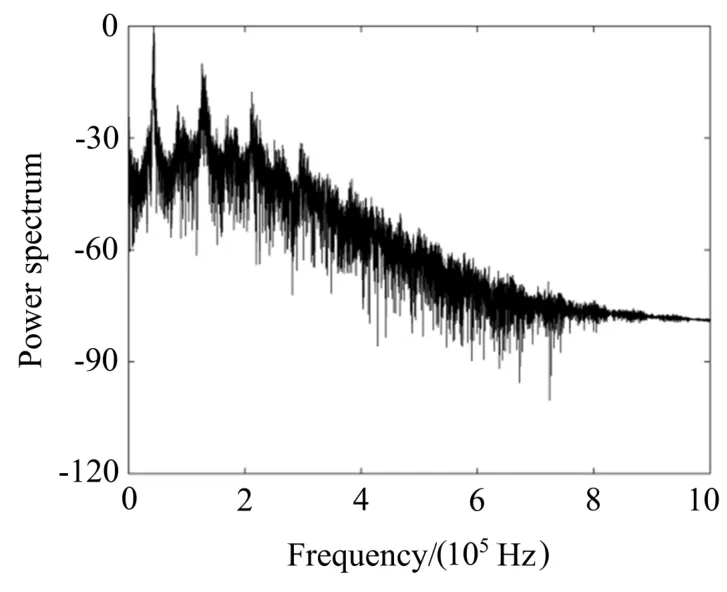
图5 系统(2)的功率谱Fig.5 Power spectrum of system(2)

1.3.4 平衡点集与稳定性分析

令系统(2)中˙x1=˙x2=˙x3=˙x4=0,即

得到系统的平衡点集为E={(x1,x2,x3,x4)|x1=x2=0,x3=α,x4=−30},其中α是任意实数,即系统(2)存在无尽的平衡点集,线性化系统(2)后可得Jacobian矩阵

将平衡点集代入JE后求得Jacobian矩阵的特征值与特征向量,第一个特征值λ1=0,特征向量e1=[0 0 0 1]T,表示系统在该平衡点集上处于亚稳态;第二个特征值λ2=0,特征向量e2=[0 0 1 0]T,表示本系统在z轴上呈收缩状态。第三和第四个特征值分别为

相应的e3,e4分别为

令(11)、(12)式的Δc=225+180α,其决定了λ3、λ4是实数还是复数,因此需要分情况讨论。当Δc>0时,此时 α > −1.25,λ3、λ4均为实数,系统的平衡点呈稳定状态;当 Δc<0时,此时 α < −1.25,λ3、λ4均为虚数,系统平衡点呈不稳定状态;当Δc=0时,α=−1.25处于临界点状态。综上,α>−1.25时,平衡点集稳定,其余情况不稳定。

2 超混沌系统的动力学特性分析

2.1 分岔特性与瞬态混沌

系统(2)拥有无限的平衡点集,故拥有无限的稳定与不稳定的平衡点,因此本系统具有多种复杂的动力学行为,例如极限环、混沌、超混沌等现象。系统参数改变会对平衡点稳定产生影响,为了更进一步地研究系统的非线性动力学特性,观察系统逐步通向混沌等的过程,研究了参数a与e改变时系统分岔图的变化情况,如图6所示。

固定参数b=15、c=30、d=3、e=0.1、k=1,取系统参数a∈(0.52,0.62),步长为0.0001,初始值选取(33,15,14,12),分岔图如图6(a)所示,揭示了本系统逐步走向混沌的过程。可见随参数a的增大,系统从周期状态出发经过多个倍周期分岔后,进入短暂的混沌状态,接着又重新进入类似周期状态,经过一段时间后进入永久混沌状态。这一阶段的有限时间尺度的混沌现象称为瞬态混沌现象,此现象是由于参数的变化,使得吸引子与吸引盆之间边界的距离慢慢变小,直到一个彼此相遇的临界值出现,这个过程使得吸引子碰触到了一个不稳定的周期轨道并引发了边界危机。

固定参数a=3,b=15,c=30,d=3,k=1,取系统参数e∈(−0.2,−0.1),步长为0.0001,初始值选取(33,15,14,12),分岔图如图6(b)所示,可见,e从−0.2出发经历了周期状态后直接进入了混沌状态,从图中可以非常明了地看到系统通向混沌的过程。

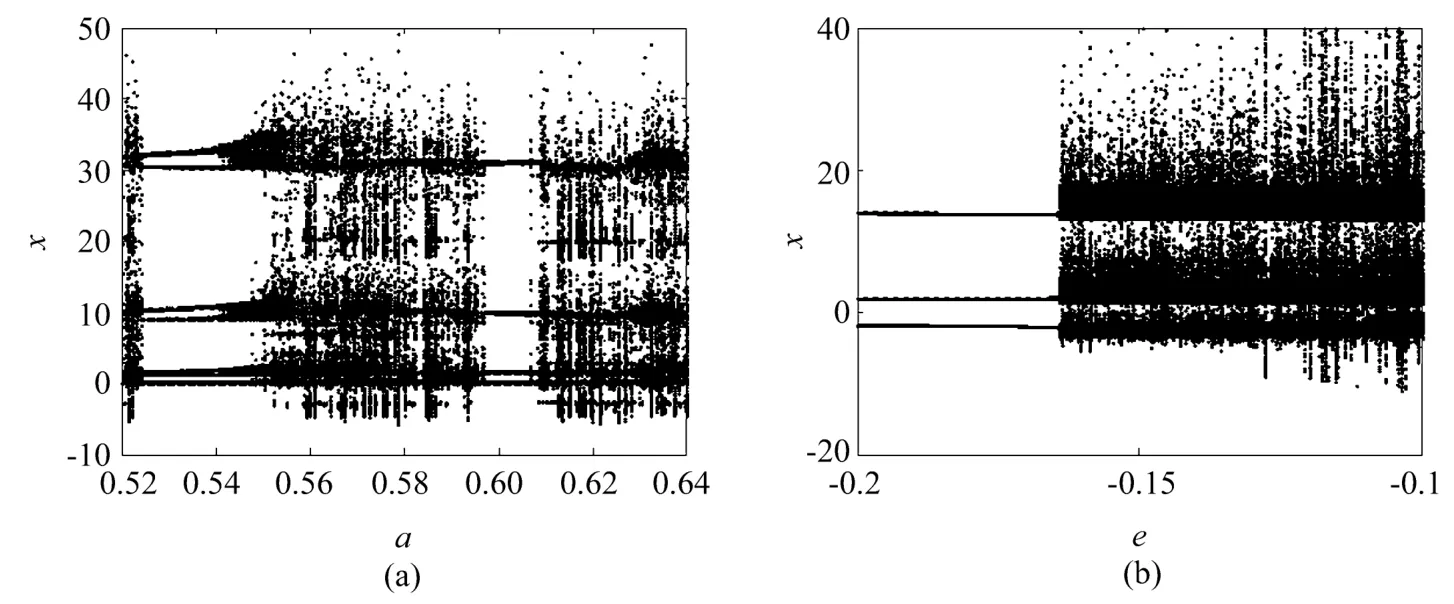
图6 随参数(a)a,(b)e变化的分岔图Fig.6 Bifurcation diagram with parameters(a)a and(b)e

2.2 多吸引子共存现象

固定原系统各参数,将初始值w作为分岔参数,当w在区域[−32,12]内变化时,得到如图7所示的Lyapunov指数谱和分岔图。从图中对比可以看出,图7(a)、(b)两图证明系统随初值w变化状态相吻合,系统从初始的发散状态出发(w=−30之前),逐步进入周期状态(w∈[−30,6]),最终进入混沌状态,表明本系统在不同的忆阻初始值状态下有着完全不同的动力学行为,这也是导致多吸引子共存现象的原因。为了更进一步证明多吸引子共存现象的存在,从该范围内取w=−22.6作吸引子相图,如图8(a)所示,为周期态;取w=10,为混沌态,如图8(b);取w=12,为超混沌状态,如图8(c)。可见当系统各参数不变时,系统状态随着初始值的变化而改变。

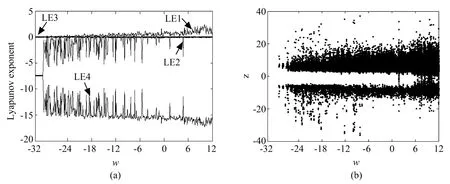
图7 (a)随w变化的Lyapunov指数;(b)w∈[−32,12]的分岔图Fig.7 (a)Lyapunov exponent with w;(b)Bifurcation diagram with w ∈ [−32,12]

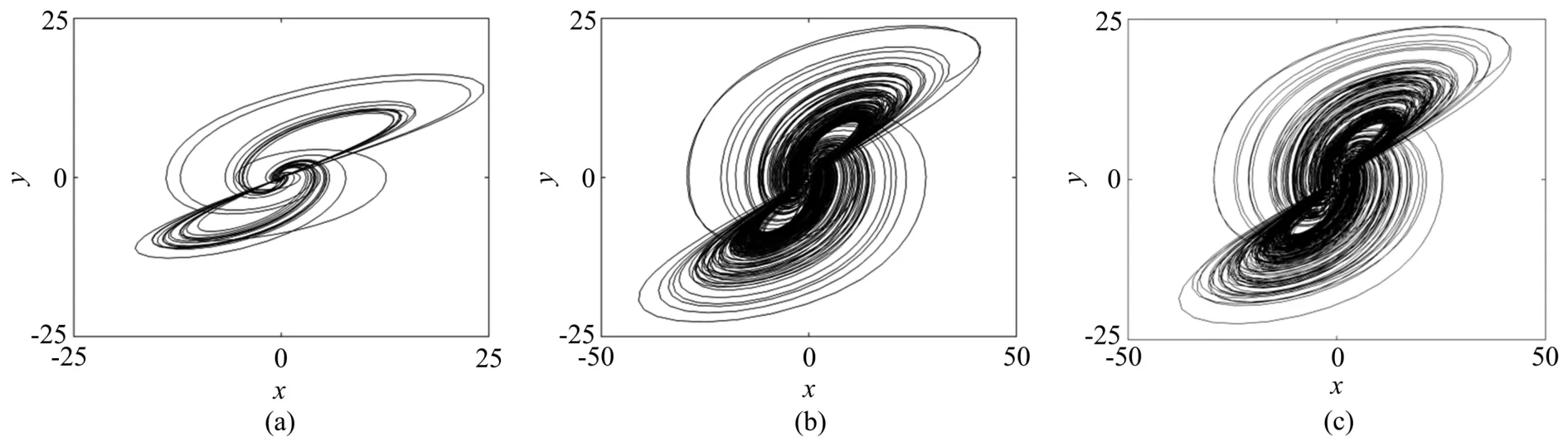
图8 随w变化的吸引子xy平面相图。(a)w=−22.6;(b)w=10;(c)w=12Fig.8 Phase portraits of attractor on xy plane with w.(a)w=−22.6;(b)w=10;(c)w=12

3 忆阻超混沌系统的电路实现

为进一步证明本系统的可行性,避免混沌退化效应,设计出了相应超混沌忆阻电路,并在示波器上观察到了相应形成的相图。为了图像整洁,分别给出了各支路的连线图,并分别用x、y、z、w代替x1、x2、x3、x4。利用改进型模块化设计方法最大程度节省了元器件的使用与工作量,并在Multisim上进行了电路仿真,图中运算放大器与电容组合实现了反向积分功能,与电阻组合实现了反相器功能,乘法器用来实现电路中的非线性项。并采用运算放大器U1、U2(LM741)、乘法器、线性电容、线性电阻等元器件构建电路。根据基尔霍夫定律可得(2)式对应的电路方程为

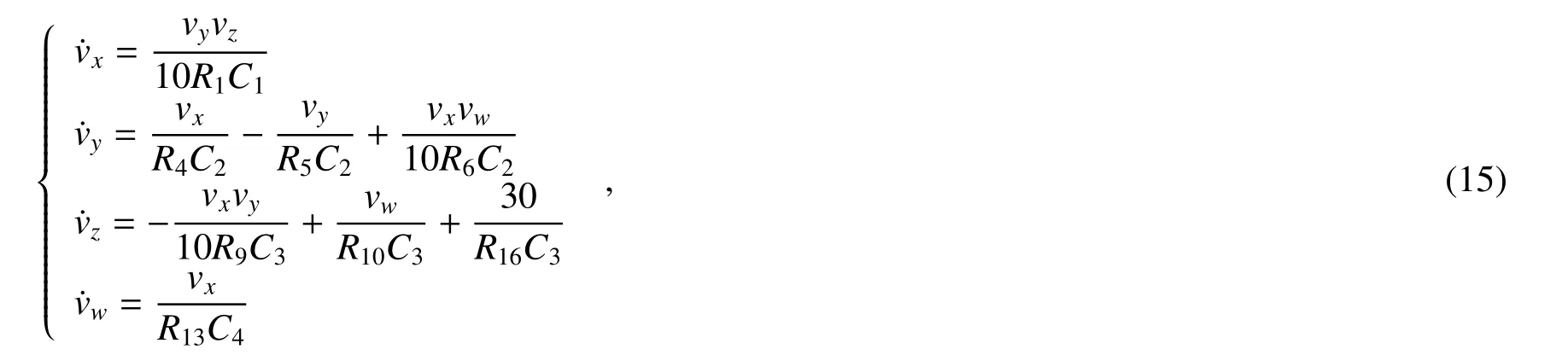
其中反相器电路中各电阻Ri(i=2,3,7,8,11,12,14,15)=10 kΩ,Ci(i=1,2,3,4)=100 nF,选取VEE,VCC=±12 V,故运放的线性工作范围为±10.6 V,需作变量比例压缩变换(此处选取10倍),令vx、vy、vz、vw代表电压,即vx=10vx1、vy=10vy1、vz=10vz1、vw=10vw1,其中vx1、vy1、vz1、vw1是积分电容上施加的电压,且采用倍乘因子为0.1的AD633乘法器,时间尺度变换因子τ0=100。经过压缩、尺度变换后的标准化方程为

计算可得到R1=333.333 Ω,R4=8.333 kΩ,R5=6.667 kΩ,R6=10 kΩ,R9=1 kΩ,R10=100 kΩ,R13=100 kΩ,R16=1 MΩ。电路原理如图9所示,其中图9(a)为x支路电路原理图;图9(b)为y支路电路原理图,线框内是忆阻器的等效电路图,其中−x经过反向积分后得到磁通量w,w经过由R100(10 kΩ)、R101(10 kΩ)、R102(10 kΩ)、R103(5 kΩ)、R104(10 kΩ)和二极管D1、D2构成的绝对值电路实现了对于忆阻器磁通量的绝对值运算。图9(c)为第二种忆阻器等效电路搭建方法,原理是利用符号函数电路与乘法器连接实现绝对值电路,其中R19=100 kΩ,C5=100 nF,R17=Esat=10.6 kΩ,R18=1 kΩ。这种方法在系统中使用元件较少,节省元件数量,值得进一步研究。图9(d)为z支路电路原理图,将其中包含的常数项看成普通参数参与设计,计算后选用V1=−30 V的接地电源表示。

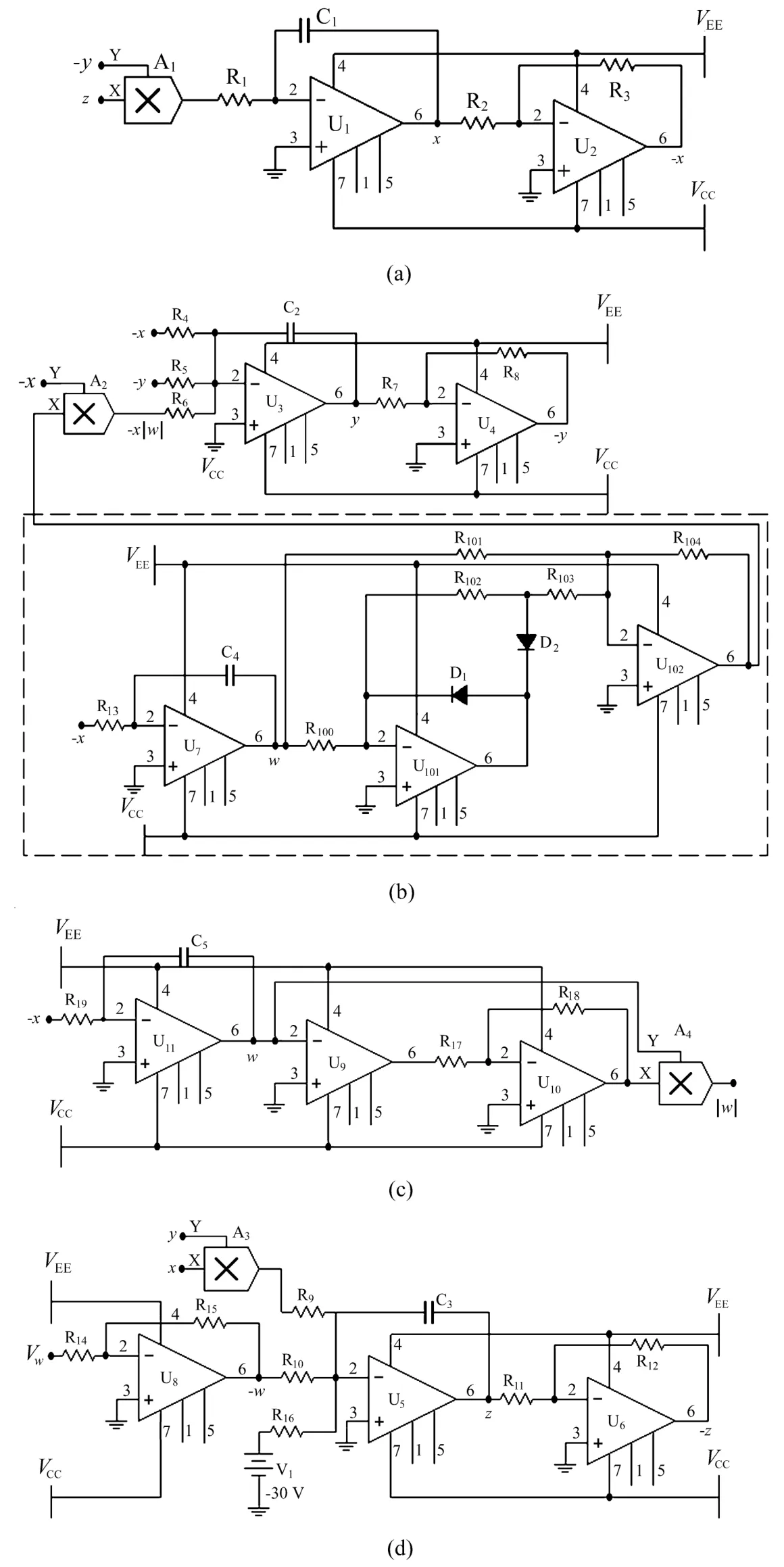
图9 (a)x支路电路;(b)y支路电路;(c)忆阻器第二种等价电路;(d)z支路电路Fig.9 (a)Circuit of branch x;(b)Circuit of branch y;(c)The second equivalent circuit of memristor;(d)Circuit of branch z

示波器仿真结果如图10所示,各平面相图均与数值仿真结果一致,验证了本系统的正确性与现实可用性。

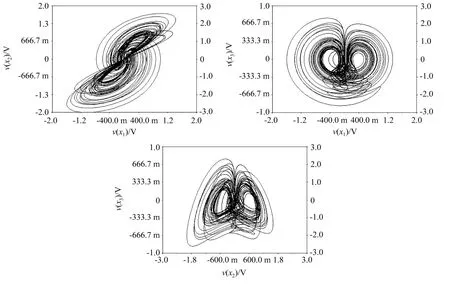
图10 示波器中得到的吸引子Fig.10 Attractors observed in analog circuit

4 结论

基于Sprott-B设计了一种新的忆阻器超混沌系统,该系统通过引入二次型磁控忆阻器,极大地增加了系统复杂性,提高了系统混沌性。通过对于系统的包括Lyapunov指数与维数、耗散性、Poincare截面与功率谱图、平衡点集与稳定性等特性的分析,从数值仿真角度证明了本系统的超混沌特性;分析了包括随参数变化的分岔图和多吸引子共存等新动力学行为,这是首次对于包含常数项的超混沌系统进行的混沌形成过程和多吸引子共存的研究;最后搭建了基于Sprott-B的超混沌忆阻电路,并用示波器观察到了吸引子相图,验证了本系统的切实可行性。第二种忆阻器等效电路在系统中虽然使用元件较少,但效果并不明显,主要表现在示波器图像失真等方面,有待进一步的研究。