State Key Laboratory of Nuclear Physics and Technology,Fusion Simulation Center,School of Physics,Peking University,Beijing 100871,People’s Republic of China

Abstract We investigate nonlinear phase dynamics of an ideal kink mode,induced by E×B flow.Here the phase is the cross phase(θc)between perturbed stream function of velocity()and magnetic field(),i.e.θc=θφ−θψ.A dimensionless parameter,analogous to the Richardson number,the normalized growth rate of the pure kink mode;normalized E×B shearing rate)is defined to measure the competition between phase pinning by the current density and phase detuning by the flow shear.When Ri＞1,θc is locked to a fixed value,corresponding to the conventional eigenmode solution.When Ri≤1,θc enters a phase slipping or oscillating state,corresponding to a nonmodal solution.The nonlinear phase dynamics method provides a more intuitive explanation of the complex dynamical behavior of the kink mode in the presence of E×B shear flow.

Keywords:kink mode,E×B flow,nonlinear phase dynamics,Richardson number

1.Introduction

In tokamaks,the plasma current contributes significantly to the inward Lorentz force as well as the existence of nested magnetic surface,which are essential to long-term confinement and equilibrium[1,2].On one hand,strong plasma current may drive instabilities,leading to the kink(e.g.ideal kink mode)or break-up of magnetic surface(e.g.tearing mode or sawtooth oscillation with finite resistivity).If these instabilities grow vigorously,they may cause a degradation of sustaining operation or even disruption[1,3,4].On the other hand,the quiescent H-mode(QH-mode)with observed benign edge harmonic oscillation is thought to be a saturated kink/peeling mode[5].Generally speaking,the currentdriven kink mode serves as a basic ideal magnetohydrodynamic(MHD)mode,and it plays a key role in the physical understanding of plasma confinement.

In the last decades,the common theoretical treatment of linear instability is to represent the temporal evolution of infinitesimal perturbations as exponential ones,and then solve the linearized equations as an eigenvalue problem.However,the limitation of this approach is that the eigenvalue can only describe the final fate of the perturbations to be stable or unstable,but fails to capture the inherent short-term behaviors in time.Specifically,in the tokamak edge region,the selfadjointness property is lost because there exists shear flow[6].As such,the conventional energy principle is no longer valid in that region[7,8].Sometimes we turn to numerical simulations or nonmodal stability analysis[9],but they are either computationally expensive or sophisticated,and they are unable to intuitively explain the underlying physics.In recent years,phase dynamics is regarded as a useful framework to describe edge MHD relaxation dynamics,which has been successfully applied to theory,experiments and simulations[10-14].It should be noted that these works are mainly based on the assumptions of constant amplitude or near marginal stable state,thus only the phase evolves over time dynamically.We aimed,hereafter,to consider the evolution of both amplitude and phase systematically,including their feedback to each other.

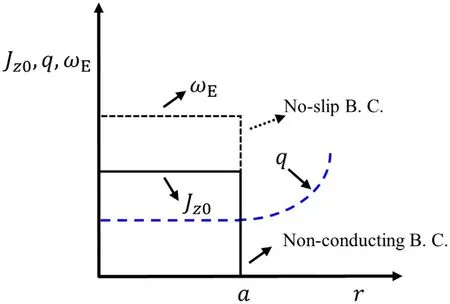
Figure 1.A schematic plot of mean current density and vorticity distributions.The current density and vorticity are constant inside of r=a,and zero outside of r=a.q is the safety factor:q=(rBz0)/(R0Bθ).Non-conducting boundary conditions and no-slip boundary conditions are used for current and vorticity,respectively.

In this work,we use the reduced MHD equations to perform the description of linear kink mode,including the E×B shear flow.Note that[10]approaches this similar topic from a transport angle,i.e.how E×B shear influences the phase dynamics of the heat flux.It is more general but cannot address the role of phase dynamics in the mode formation,which is crucial to obtain a more precise prediction of the transport process.Our new work considers an explicit mode(here,the kink mode),which is a general theory of kink mode and shear flow interactions.We first introduce our nonlinear phase dynamics model and benchmark its results with the conventional eigenvalue method in section 2.Then we investigate the effects of flow shear on kink mode in section 3,trying to improve the comprehension of kink mode in the edge plasmas.Finally,brief conclusions and discussions are made in section 4.

2.Nonlinear phase dynamics model

For analytical simplicity,we choose a cylindrical system of coordinate r,θ and z to describe the kink mode.The model we used includes the reduced MHD equations:[1,8]

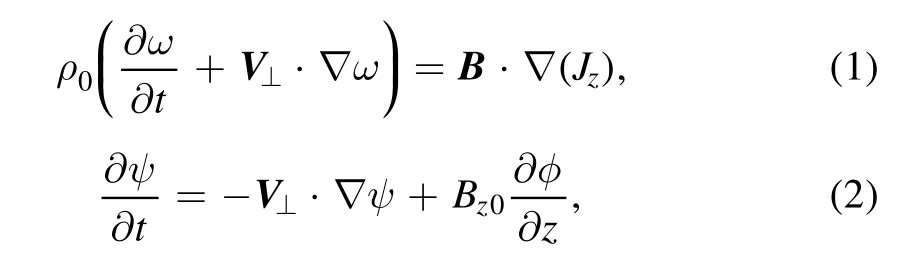
where the mean longitudinal field Bz0and densityρ0are considered as constant and ‘⊥’ indicates perpendicular to z direction.These equations are closed by the subsidiary relations:

In which the vorticity(ω)is related to the E×B shearing rate.To study the linear kink mode,we decompose the physical quantities into mean parts(marked as subscript ‘0’)and infinitesimal perturbative parts(marked as),i.e.For perturbations,where 2πR0is the length of the straight cylinder with identical ends.θc=θφ−θψis defined as their cross phase.The mean current density and vorticity are treated as uniform distributions(i.e.in figure 1),in which two solutions are possible.One is related to the well-known Alfvén waves,and the other one links to kink instability[1]:i.e.

The solution of equation(5)isin which α and β entail the plasma boundary perturbation.Suppose that the plasma column is not surrounded by a conducting shell,the inner and outer boundary conditions areandrespectively.Atthen we can write:

Thefunction looks similar.By integrating equation(1)over the narrow interval around r=a,and separating the real part and imaginary part,the linearized form of equations(1)and(2)at r=a can be recast as:

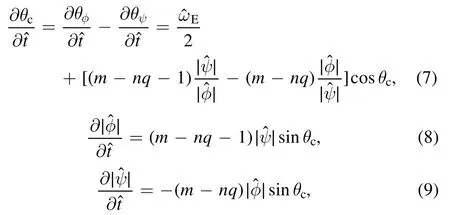
3.Synergistic effects of current and E×B shear flow(phase bifurcation)

When the E×B shear flow is considered,we find that the larger E×B shearing ratethe smaller modified kink growth rate(γ2)(figure 3).It means that the flow shear has a stabilizing effect on the kink mode,and here the critical shearing rate for transition to a stable state isThen we define a dimensionless parameterfor quantitative investigation,which is analogous to the Richardson number in stratified fluids[15].For further simplification,equations(7)-(9)can be reorganized as:

Figure 2.Growth rate of ideal pure kink mode for uniform mean current density distribution,here the shear flow is excluded.

In order to find a steady state,one possibility is to letThen we solve,which is thefamous Adler equation and form ofthe Kuramotomodel[16,17].There exist two types of solutions:

and

Figure 3.Growth rate of ideal kink mode in the presence of E×B shear flow,here m=2 and nq(a)=1.5.

Phase lock state is an unstable state and phase slip state is an oscillating stable state with a periodic oscillation timeWhen the shearing rateis small(i.e.Ri＞1),phase lock exists,which means θcevolves to a fixed value and the amplitude grows exponentially(figure 4(a)).When the shearing rate is above the critical value(i.e.Ri≤1),phase slip occurs,in which the amplitude oscillates and θcslips with time periodically(figure 4(b)).

Another possibility for steady sate solution is to letsinThen we solveviz.,

As Famp,2should be positive,only θc=0 is a possible steady state solution.Forwe carry out asymptotic expansion with small perturbation.That is,assumingwe can get:

Figure 4.(a)Weak shear,phase lock state,where m=2,nq(a)=1.5,Famp=1 and Ri=4/0.36＞1.(b)Strong shear,phase slip state,where m=2,nq(a)=1.5,Famp=1 and Ri=4/4.84 ＜1.

Figure 5.(a)Strong shear,stable state,where m=2,nq(a)=1.5,Famp=1.558(0.6413)and Ri=4/4.84 ＜1.(b)Strong shear,phase oscillating state,where m=2,nq(a)=1.5,Famp=2 and Ri=4/4.84 ＜1.

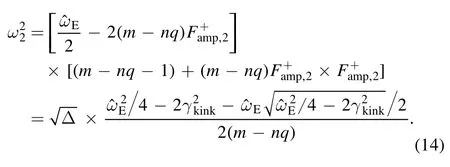
An enlightening way to understand these phenomena above is by using the potential concept[18],i.e.

Figure 6.Phase potential of(a)phase lock state,(b)phase slip state and(c)phase oscillating state.

wherePθcand Pampare ‘phase potential’ and ‘amplitude potential’,respectively.‘δ’ stands for small variance in variational principle.From the‘phase potential’,we can see that in phase lock state,the cross phase is trapped in the potential well(figure 6(a)).In phase slip state,the potential well is flattened,so that the cross phase can slip along the slope with time periodically(figure 6(b)).In phase oscillating state,the potential well changes with time periodically.Once the cross phase wants to escape from the potential well,the barrier is going to get deeper so as to kick the cross phase back to the potential well.During this stage,the cross phase moves periodically in the potential well(figure 6(c)).These consistent features can also be found in ‘amplitude potential’.

4.Conclusion and discussion

To date,we employ the nonlinear phase dynamics method to investigate the impact of E×B shear flow on ideal linear kink mode,which is in the simplification of uniform current density for theoretical analysis.The amplitude and phase are both evolving over time systematically.Firstly,we illustrate that this method could give the same growth rate as the conventional eigenvalue method in the absence of shear flow.Secondly,we find that the E×B flow shear could stabilize the kink mode,and by increasing shearing rate could decrease the growth rate.Furthermore,we define a dimensionless parameterfor quantitative investigation,whereand γkinkare the normalized shearing rate and growth rate of pure kink mode,respectively.On the one hand,if the flow shear is weak(i.e.Ri＞1),the cross phase between perturbed stream function of velocity()and magnetic field()is locked to a fixed value and the amplitude grows exponentially(eigenmode solution).On the other hand,if the flow shear is strong enough(i.e.Ri≤1),the cross phase slips or oscillates periodically,leading to an amplitude-oscillating steady state(nonmodal solution).Last but not least,the phase(amplitude)potential concept could help us understand the underlying physics more intuitively.

Right now our theory is succinct because both the current and E×B flow shear are treated as constant,but it is instructive and provides a physical insight into the linear analysis.We expect these concepts and techniques could open a new road to enrich the physical understanding of linear instabilities.Moreover,it can be used to explore the explanation and prediction of some related experimental phenomena.For more realistic scenarios,such as nonuniform profiles,the spatial coupling of the phases gets important.Some results have been reported in a recent work[19].To progress beyond the scope of this paper,theoretical and numerical investigation of nonuniform profiles,wall effects and nonlinear effects will be our future work.

Acknowledgments

We would like to thank the referees for constructive comments and acknowledge P H Diamond,X Q Xu,D Hu,Z J Mao,C Meng and Y Lang for useful physical discussions.We are also grateful to W M Chen,Z Y Li,Y Y Yu,B Gui and G Q Dong for useful technical help.We acknowledge fruitful interactions with participants in the Festival de Théorie,Aix-en-Provence(2019).This project was supported by the National MCF Energy R&D Program of China(No.2018YFE0311400)and the numerical simulations were supported by the High-performance Computing Platform of Peking University.