管训贵

(泰州学院 数理学院，江苏 泰州 225300)

0 引言及主要结论

设D>2是不能被6k+1型素数整除的无平方因子正整数。文献[1-3]对于较小的正整数m讨论了方程

x3±33m=Dy2，gcd(x,y)=1

(1)

的求解问题。本文证明了以下一般性的结果。

定理1不定方程(1)有正整数解(m,x,y)的充要条件是方程

(2)

由定理1直接可得

推论1若2|D，2|/m，或2|/D，2|m，则不定方程x3+33m=Dy2，gcd(x,y)=1无整数解；若2|D，2|m，或2|/D，2|/m，则不定方程x3-33m=Dy2，gcd(x,y)=1无整数解。

推论2若D含有素因子p，满足p≡5(mod 12)，则不定方程(1) 无正整数解。

推论3不定方程x3+27=11y2满足gcd(x,y)=1的正整数解仅有(x,y)=(8,7)；不定方程x3-729=47y2满足gcd(x,y)=1的正整数解仅有(x,y)=(56,61)。

1 若干引理

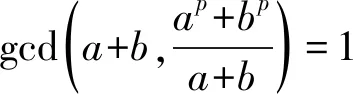
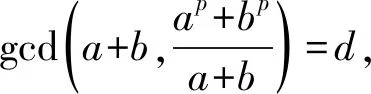
即

(3)

(4)

下证gcd(d,a)=1。因为若设gcd(d,a)=d1>1，则d1有素因数q，使得q|d，q|a。 而d|(a+b)，故q|(a+b)，推得q|b，与gcd(a,b)=1矛盾。因此gcd(d,a)=1。此时由(4)式得d|p，所以d=1或p。 引理1得证。

证明参见文献[4]。

由引理2立得

证明参见文献[5]。

2 定理1的证明

1)先证必要性。设(m,x,y)是方程(1)的正整数解，则(1)式成为

(x±3m)(x2∓3mx+32m)=Dy2。

(5)

因为gcd(x,y)=1，所以由(1)式知3|/D且3|/x，从而x±3m≢0(mod 3)。根据引理1得gcd(x±3m,x2∓3mx+32m)=1。 设p|D，则p=2或p≡5(mod 6)，故由引理3知，p|/(x2∓3mx+32m)。于是(5)式可化为

x±3m=Da2，

(6)

x2∓3mx+32m=b2，

(7)

这里a,b都是正整数，满足gcd(a,b)=1且y=ab。由(6)，(7)两式可得(2Da2∓3m+1)2+32m+1=(2b)2,即

(2b+2Da2∓3m+1)(2b-2Da2±3m+1)=32m+1。

(8)

注意到2b+2Da2∓3m+1与2b-2Da2±3m+1不能同时被3整除，否则有3|4b,3|2(2Da2∓3m+1)，即3|b,3|a,与gcd(a,b)=1矛盾。故(8)式可化为

(9)

或

(10)

当(9)式成立时，由(9)式可解出

(11)

(x,y)=(Da2∓3m,ab),

3 推论的证明

先证推论1。

再证推论2。

由定理知，方程(1)有正整数解(m,x,y)的充要条件是方程(2)有正整数解(m,a)，且D的奇素因子p都满足p≡11(mod 12)。若D含有素因子p满足p≡5(mod 12)，则不定方程(1) 必无正整数解。推论2得证。

最后证推论3。