福建省南平市高级中学(353000) 江智如 江 伟 蔡 珺

1 问题提出

三角、导数是高考的必考内容,一个侧重基础,一个侧重压轴,考查考生的数学基础水平与思维深度.二者的交汇融合是近年高考及各类模拟考的常客,常考常新,是冰与火的碰撞.由于函数表达式为三角函数与其它初等函数的复合,无论怎么求导函数,都会出现含三角函数且较为复杂的函数表达式.解决此类问题,需要利用三角函数性质、分离参数、分类讨论、构造函数等方法来处理,涉及函数隐零点、极值点偏移等相关知识与技巧.总结归纳此类问题的有效解题思路与方法,能够帮助考生破解困惑,拓宽数学视野,同时也能践行新高考从“能力立意”向“素养导向”转变的理念与要求[1],提升考生的学科素养.

2 概念界定

本文探究以三角函数为载体的函数模型归纳为四种模型:(1)f(x)=ax+Asin(ωx+φ) 或f(x)=ax+Acos(ωx+φ)模型;(2)f(x)=或f(x)=模型;(3)f(x)=x·sinx或f(x)=x·cosx模型;(4)f(x)=alnx+bsinx或f(x)=aex+bsinx模型.它们是函数性质的综合应用,难度大,对考生的函数基础知识和综合应用能力要求较高[2],体现试题的区分与选拔功能.为此,笔者在素养导向指引下探究此类问题的有效解题策略.

3 方法探析

根据2017年版《课程标准》对函数知识的要求,我们根据三角函数的性质研究这几类函数模型的图象,运用三角函数公式化简函数,利用导数研究函数性质的方法步骤求解,同时也可以巧用特殊三角不等式,如|sinx|≤|x|≤|tanx|,x ∈放缩和构造函数,从而更好地认清它们的本质,做到“有图在心中,解题很轻松”.

3.1 基于f(x)=ax+A sin(ωx+φ) 或f(x)=ax+A cos(ωx+φ)模型

题目1(2016年高考全国课标Ⅰ卷文第12 题)若函数f(x)=x-sin 2x+asinx在(-∞,+∞)单调递增,则a的取值范围是( )

A.[-1,1] B.C.D.

解析由题意可知,

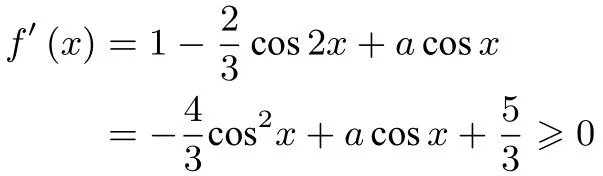
对x∈R 恒成立,令t=cosx,考虑g(t)=对t ∈[-1,1]恒成立,从而由二次函数图象性质得解得故选C.

评析本试题以函数单调性作为背景,依托三角函数性质为载体考查含参函数恒成立问题,需要考生能够敏锐地利用二倍角的余弦公式,把函数转化为关于余弦的二次函数模型,再利用换元法,借助二次函数的图象,运用数形结合思想,快速地求出a的取值范围.考查考生化归与转化思想,数形结合思想,逻辑推理能力、运算求解能力,充分考查了考生对有关初等导函数基本知识的掌握程度,又考查了考生综合应用基本方法解决问题的能力,渗透逻辑推理、直观想象和数学运算素养的考查.

方法总结“千淘万漉虽辛苦,吹尽狂沙始到金”,此类模型依托函数与方程思想,利用三角函数恒等变换和导数研究函数性质的方法,分离参数,借助函数图象,列出等价方程(组)或不等式(组)进行求解.解题步骤归纳为:(Ⅰ)求导,恒等变换;(Ⅱ)构造函数,画出函数图象草图;(Ⅲ)根据图象,确定特殊点,列出等价不等式组;(ⅠV)求出参数的取值范围;也就是“一变,二画,三列式”[5].

变式1(2019 高考课标Ⅰ卷文科第12 题) 已知函数f(x)=2 sinx-xcosx-x,f′(x)为f(x)的导数.

(Ⅰ)证明:f′(x)在区间(0,π)存在唯一零点;(Ⅱ) 若x∈[0,π]时,f(x)≥ax,求a的取值范围.

解析(Ⅰ)设g(x)=f′(x),则g(x)=cosx+xsinx-1,从而g′(x)=xcosx.容易知道当x∈时,g′(x)＞0;当x∈时,g′(x)＜0,所以g(x)在单调递增,在单调递减.又g(0)=0,＞0,g(π)=-2,故g(x)在(0,π)存在唯一零点,所以f′(x)在(0,π)存在唯一零点.

(Ⅱ)由(Ⅰ)知,f′(x)在(0,π)只有一个零点,设为x0,且当x∈(0,x0)时,f′(x)＞0;当x∈(x0,π)时,f′(x)＜0,所以f(x)在(0,x0)单调递增,在(x0,π)单调递减.又f(0)=0,f(π)=0,故当x∈[0,π]时,f(x)≥0.据题意,当x∈[0,π]时,f(x)≥ax,因此,a的取值范围是(-∞,0].

评价本题分步设问,第(Ⅰ)问既考查了导数在研究函数性质中的应用,又为第(Ⅱ)问做了铺垫,使问题逐步推进.第(Ⅱ)问则将函数与不等式有机结合,考查由浅入深,对计算难度、思维深度的要求逐步提高,重点突出、层次分明,达到考查目的.试题从多角度考查导数的基础知识及利用导数研究函数性质的方法,对考生的逻辑推理能力、运算求解能力、分类与整合的思想提出了较高的要求,体现区分度,使考生个体理性思维的广度和深度得到了充分展示,考查考生进一步数学学习的潜能[4],促进数学学科素养的提升.

3.2 基于f(x)=或f(x)=模型

题目2(2014年高考北京卷理科第18 题) 已知函数f(x)=xcosx-sinx,x∈

(Ⅰ)略;(Ⅱ)若a＜＜b对x∈恒成立,求a的最大值和b的最小值.

解析(Ⅰ) 略;(Ⅱ) 当x∈时,a＜等价于sinx-ax＞0;＜b等价于sinx-bx＜0;令g(x)=sinx-cx,则g′(x)=cosx-c.当c≤0 时,g(x)＞0对任意x∈恒成立;当c≥1 时,g′(x)＜0 对任意x∈恒成立,所以g(x)在区间上单调递减,从而g(x)＜g(0)=0 对任意x∈恒成立;当0＜c＜1时,存在唯一的x0∈使得g′(x0)=cosx0-c,当x∈(0,x0) 时,g′(x)＞0,此时g(x)＞g(0)=0;当x∈时,g′(x)＜0.故g(x)＞0 对任意x∈恒成立,当且仅当即0＜c≤综上所述,当且仅当c≤时,g(x)＞0 对任意x∈恒成立;当且仅当c≥1 时,g(x)＜0 对任意x∈恒成立;所以a＜＜b对x∈恒成立,a的最大值为b的最小值为1.

评价本题主要考查导数的运算、不等式证明、运用导数研究函数的性质等基础知识和方法.利用导数判断函数的单调性,构造出函数g(x)=sinx-cx是解题的关键,考查由浅入深,对计算难度、思维深度的要求逐步提高,考查层次分明,重点突出,较好地达到了考查目的.试题从多维度考查了导数和三角函数的基础知识及利用导数研究函数性质的方法,同时对考生逻辑推理能力、运算求解能力、分类讨论与整合的能力提出了较高要求,尤其是对逻辑推理能力的考查,层次分明,区分度较高,使考生个体理性思维的广度和深度得到了充分展示,较好地考查了考生进一步学习的潜能,提升学科素养.

方法总结“化归醲粹兮复胥庭”,此类模型以分式型复合函数为载体,依托化归与转化的思想,把分式模型等价转化为整式模型,利用导数研究函数性质的方法,分类讨论,等价转化为含参恒成立问题求解.解题步骤归纳为:(Ⅰ)化归恒等变换为整式模型;(Ⅱ)构造函数;(Ⅲ)求导分类讨论,得到等价方程(组)或不等式(组);(ⅠV)运算求解,得到结果;也就是“一整,二构,三列式”.

变式2(2020年湖南邵阳一模理科第22 题)已知函数f(x)为反比例函数,曲线g(x)=f(x)cosx+b在x=处的切线方程为

(Ⅰ)求g(x)的解析式;(Ⅱ)判断函数F(x)=g(x)+1-在区间(0,2π]内的零点的个数,并证明.

解析(Ⅰ)容易求得g(x)=-1;(Ⅱ) 因为所以又当x∈时,F′(x)＜0,故F(x)在上单调递减,又故F(x) 在上只有一个零点;当x∈时,cosx＜0.从而F(x)＜0,故F(x) 在上无零点;当x∈时,令h(x)=xsinx+cosx,则h′(x)=xcosx＞0,从而h(x) 在上单调递增.又h＜0,h(2π)＞0,故存在x0∈使得h(x0)=0,从而在上h(x)＜0,即F′(x)＞0,所以F(x)在上单调递增;在(x0,2π]上h(x)＞0,即F′(x)＜0,所以F(x) 在(x0,2π]上单调递减.由于F(2π)=0,F＜0,故F(x)在上有2 个零点,综上所述,函数F(x)在(0,2π]上有3 个零点.

评价本题第(Ⅰ)问难度不大,考查反比例函数知识与导数切线的定义,考查考生数学基础知识和运算求解能力;第(Ⅱ)问以三角函数为载体,考查函数零点问题.试题的设置使得考生需要了解函数零点存在定理,从而引导考生利用分类与整合的思想,讨论F(x)的单调性,才能得到零点的个数,对考生运用所学知识寻找合理的解题策略与推理论证能力都提出了较高要求,突出了选拔功能.

3.3 基于函数f(x)=x·sin x 或f(x)=x·cos x 模型

题目3(2018年北京东城区一模理科第20 题)已知函数f(x)=xsinx+acosx+x,a ∈R.

(Ⅰ)(Ⅱ)略;(Ⅲ)当a＞2 时,若方程f(x)-3=0 在区间上有唯一解,求a的取值范围.

解析(Ⅲ) 当a＞2 时,f′(x)=(1-a)sinx+xcosx+1.设h(x)=(1-a)sinx+xcosx+1,则h′(x)=(2-a)cosx-xsinx,因为a＞2,x∈所以h′(x)＜0.从而h(x)在区间上单调递减.又h(0)＞0,h=2-a＜0,故存在唯一的x0∈使h(x0)=0,即f′(x0)=0.所以f(x) 在区间[0,x0]上单调递增,在区间上单调递减.由于f(0)=a,且方程f(x)-3=0 在区间上有唯一解,故2＜a≤3,因此a的取值范围是(2,3].

评价在高中阶段,引进导数概念,有利于学生更深刻地理解不断动态变化的事物本质,提高思维层次.导数的重要应用之一是利用导数讨论函数的单调性、极值和最值,是高中阶段的重要知识之一[6],为考生进一步学习打好扎实的基础.本题主要考查利用导数研究函数性质的方法,不等式的性质与推导方法,闭区间上连续函数零点存在性定理,从多角度考查了考生导数与三角函数的基础知识,同时对考生的逻辑推理能力、运算求解能力、分析归纳能力,以及化归与转化的数学思想方法.试题层次分明、内容丰富、区分度较高,使不同考生的理性思维的广度和深度得到了充分展示,促进考生的数学学科素养得到提升.

方法总结“行到水穷处,坐看云起时”,此类模型以函数与方程解为载体,利用分类讨论思想,运用函数介值定理和三角函数知识,结合函数图象,得到参数的范围.解题步骤为:(Ⅰ)求导构造;(Ⅱ)分类讨论;(Ⅲ)结合图象,确定关键点,列出等价不等式组;(ⅠV)求出参数的取值范围;也就是“一化,二分,三列式”.

变式3(2020年吉林省二模理科第21 题) 已知函数为f(x)的导数.

(Ⅰ) 证明:f′(x) 在区间上不存在零点;(Ⅱ) 若f(x)＞kx-xcosx--1 对x∈恒成立,求实数k的取值范围.

解析(Ⅰ)由题意得,f′(x)=令g(x)=sinx-则g′(x)=令g′(x)=0,因为x∈所以x=当x∈时,g′(x)＞0,g(x)单调递增;当x∈时,g′(x)＜0,g(x)单调递减.又故g(x)＞0 在上恒成立,即f′(x)＞0 在上恒成立,因此f′(x)在区间上不存在零点;(Ⅱ)由f(x)＞kx-xcosx--1,得sinx＞kx-1.因为x∈所以k＜令h(x)=则h′(x)=令m(x)=xcosx-sinx-1,则m′(x)=-xsinx＜0 恒成立,从而m(x)在上单调递减,故m(x)＜m(0)=-1＜0,即h′(x)＜0 在上恒成立,所以h(x) 在上单调递减,从而于是k≤因此k的取值范围是

评价导数的概念、导数的计算与应用是高中数学的重要内容,也是学生今后工作和学习的重要工具[6].试题基于y=x·cosx模型,分两步设问,逐步推进,考查由浅入深,对计算难度、思维深度的要求逐步提高,考查层次分明,能较好地达到考查目的.第(Ⅰ)问考查导函数的零点问题,考查了利用导数研究函数性质以及函数介值定理的基础知识和解题方法,考查逻辑推理能力、运算求解能力.第(Ⅱ)问考查参数恒成立问题,考查分离参数方法,考查化归与转化思想,运算求解能力,对考生的数学综合素养要求较高.本题涉及三角函数与导数的概念和性质很基本,但考查深入,为考生解答提供广阔的发挥空间,具有区分度,突出选拔功能.

3.4 基于函数f(x)=a ln x+b sin x 或f(x)=aex+b sin x 模型

题目4(2020年金太阳5月模拟文科第21 题)已知函数f(x)=lnx+xsinx.

(Ⅰ) 证 明:f′(x) 在 区 间上存在唯一的零点;(Ⅱ) 证明:对任意的x∈(0,+∞),都有f(x)＜2xlnx+x(1+sinx).

解析(Ⅰ) 设g(x)=f′(x)=+sinx+xcosx,则g′(x)=+2 cosx-xsinx.因为x∈所 以g′(x)＜0,故g(x) 在上单调递减.又故由介值定理知,g(x) 在区间上存在唯一的零点,因此原命题成立;(Ⅱ) 要证明f(x)＜2xlnx+x(1+sinx),即证(2x-1)lnx+x＞0.当x=时,不等式显然成立;当x＞时,即证lnx+＞0;当0＜x＜时,即证lnx+＜0.令h(x)=lnx+则h′(x)=当x＞时,在上,h′(x)＜0,h(x)单调递减;在(1,+∞)上,h′(x)＞0,h(x)单调递增,此时h(x)min=h(1)=1＞0,即lnx+＞0.当0＜x＜时,在上,h′(x)＞0,h(x) 单调递增;在上,h′(x)＜0,h(x) 单调递减,此时h(x)max=＜0,即lnx+＜0.综上所述,对任意的x∈(0,+∞),都有f(x)＜2xlnx+x(1+sinx).

评价指对函数是高中阶段重要的初等函数之一,与三角函数的结合增加试题的复杂性,提高难度,体现试题的区分度与选拔性.本题第(Ⅰ)问面向大部分考生,依托函数零点问题,考查导数研究函数单调性知识,函数介值定理基本知识和基本方法.重视数学基础、重视从能力立意向素养导向的转变,考查考生三角函数性质的主干知识和基本方法,要求考生具有扎实的函数知识及运算求解能力.第(Ⅱ) 问要求考生具有较高的逻辑推理能力,运用分析法,执果索因,把问题等价转化为(2x-1)lnx+x＞0,构造函数h(x)=lnx+分类讨论,通过求导,判断h(x)的单调性,把不等式问题转化为h(x)的最值问题,最终证明结论.对考生化归与转化思想、分类与整合思想、推理论证能力、运算求解能力有一定的要求,有利于发挥考生的综合水平,重视对数学素养的考查.

方法总结“曲径通幽处,禅房花木深”,此类模型以指对函数与三角函数的基本知识和性质为载体,考查函数单调性和最值问题.可以通过分析法,执果索因,明确问题的方向,然后等价变化,构造函数,利用导数方法求解.解题步骤为:(Ⅰ)分析推理;(Ⅱ)等价变化;(Ⅲ)构造函数;(ⅠV)最值求解;也就是“一析,二变,三构造”.

变式4(2020年河南高考仿真模拟理科第21 题)已知函数f(x)=e|x|-3 cosx.

(Ⅰ) 证明:f(x)+2≥0;(Ⅱ) 当x∈时,不等式m＜＜n恒成立,求实数m的最大值和n的最小值.

解析(Ⅰ) 当x∈[0,+∞) 时,f(x)=ex-3 cosx,则f′(x)=ex+3 sinx.当x∈[0,π)时,f′(x)＞0,f(x)单调递增;当x∈[π,+∞)时,f′(x)=ex+3 sinx≥ex-3＞0,f(x) 单调递增.所以f(x) 在[0,+∞) 上单调递增,从而f(x)≥f(0)=-2,故f(x)+2≥0,又f(x) 为偶函数,因此对x∈R,f(x)+2≥0 均成立;(Ⅱ) 由题条件化简得,当x＞0 时,问题等价于

令g(x)=sinx-tx,则g′(x)=cosx-t.当t≥0时,在x∈上,g′(x)＞0,故g(x) 在上单调递增,则g(x)＞g(0)=0,所以t≥0;当t≥1 时,在x∈上,g′(x)＜0,故g(x)在上单调递减,则g(x)＜g(0)=0,所以t≤1;当0＜t＜1 时,存在唯一的x0∈使得g′(x0)=cosx0-t=0,当x0∈(0,x0)时,g′(x)＞0;当x0∈时,g′(x)＜0;故g(x)在(0,x0)上单调递增,在上单调递减,则g(x0)＞g(0)=0,所以当x∈时,g(x)＞0 恒成立,当且仅当即0＜t≤综上所述,当且仅当0＜t≤时,g(x)＞0 在x∈上恒成立;当且仅当t≥1 时,g(x)＜0 在x∈上恒成立;因此m的最大值为n的最小值为1.

评价本题第(Ⅰ)问的设计面向大部分考生,以不等式为载体,考查函数的最值问题.考生在分析理解函数f(x)奇偶性的基础上,利用导数和正弦函数的性质,求解f(x)的值域.考查分类与整合的思想、逻辑推理能力、运算求解能力.第(Ⅱ)问选取含有参数的不等式为条件,求解参数的最值,以此考查考生的运算求解能力和逻辑推理能力.要求考生灵活应用知识,将不等式迁移到不同情境中,构造函数g(x)=sinx-tx,通过讨论g(x)的单调性,利用g(x)的取值范围,根据恒成立关系得到参数m和n的最值,充分考查分类讨论、化归与转化的思想.

4 探究展望

以三角函数为载体的四类函数模型的解题思路可以总结为:“一构造,二讨论,三判断”,解决的关键在于通过求导构造函数,分离参数,转化为函数恒成立[7]、极值点偏移[8]等问题,运用分类与整合的思想,结合函数图象求解,需要考生扎实的数学基础和综合应用能力,体现考生继续学习的潜能.此外在解决此类问题时,我们可以结合三角函数的性质和公式进行求解,会起到事半功倍的效果.三角和导数也是高中数学与高等数学的一个连接点,贯穿整个数学知识体系,从导数的视角理解含三角函数的综合问题,可以更加深入理解问题的本质,弄清问题的来龙去脉,依托合理的“精致练习”[9]训练学生导数综合应用能力,能够拓宽考生的数学视野,培养考生正确的数学学习方法,激发考生进一步学习的潜能,促进考生数学学科素养的提升.