曾 娇，崔泽建

（1.宜宾学院数学学院，四川宜宾644007；2.西华师范大学数学与信息学院，四川南充637009）

含色散长波方程组是由描写均匀不可压缩流体运动的浅水（或长波）方程组变形而来，在浅水（或长波）方程组的第一个方程左端加上色散项，则为Boussinesq 方程组，同时在第二个方程左端也加上色散项，则可得到含色散长波方程组：

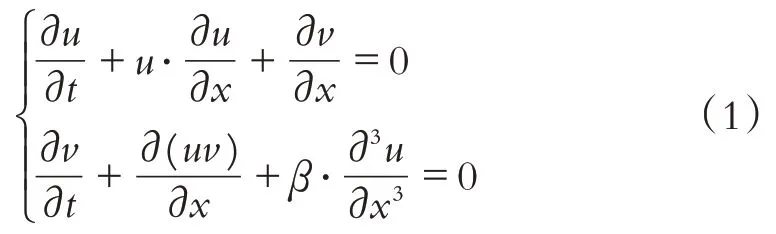
其中：β为色散系数.

众多学者对求解非线性发展方程的精确解进行了不懈的努力，采用了齐次平衡法[1]、双曲函数法[2]、Jacobi 椭圆函数展开法[3]等方法. 尤其值得关注的是2008 年由Wang 等成功创立的展开法[4]，并在此之后，很多学者对展开法进行改进和推广，衍生出展开法[7]等方法.之前已有学者对含色散长波方程组进行求解[8]，但所得的解形式局限，因此本文拟用推广的展开法求解含色散长波方程组的精确解，以期丰富含色散长波方程组的解系.

假设含两个独立变量x、t的非线性偏微分方程（PDE）一般形式为：

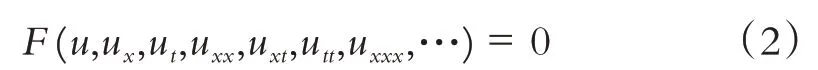
其中F为含有u和u的各阶导数的多项式，u=u(x,t)是未知函数，引入行波变换

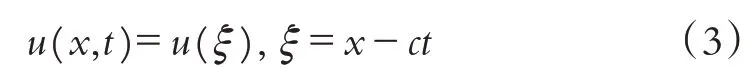
将（3）代入（2）得到关于u=u(ξ)的常微分方程：

这里“′”表示

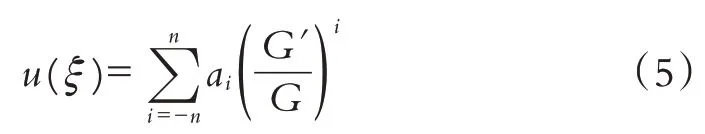
其中G=G(ξ)满足二阶线性微分方程：

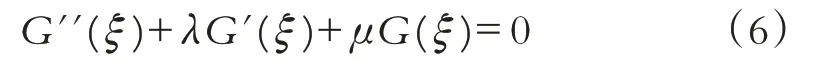
式（5）中的a0,a1,a2,…,an和式（3）中的c均为待定常数，整数n由（4）中的非线性项和最高阶导数项平衡来确定.

由于已知方程（6）的解，将上面所得的结果带回（5）式，即得非线性偏微分方程（2）的精确行波解.

2 含色散长波方程组的精确解

用行波变换（3）代入含色散长波方程组（1），得到关于u=u(ξ)的常微分方程组：

方程(7a)对ξ积分可得：

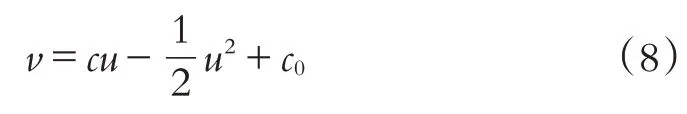
其中c0为积分常数.

将（8）式代入方程(7a)可得：

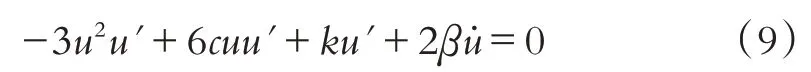
其中k=2(c0-c2).

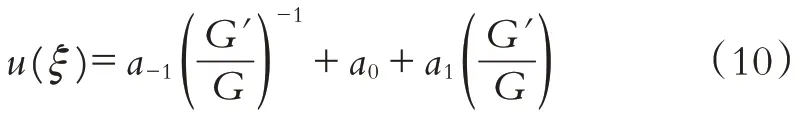
利用MATLAB求解上述方程组可得到两组解.第一组解：

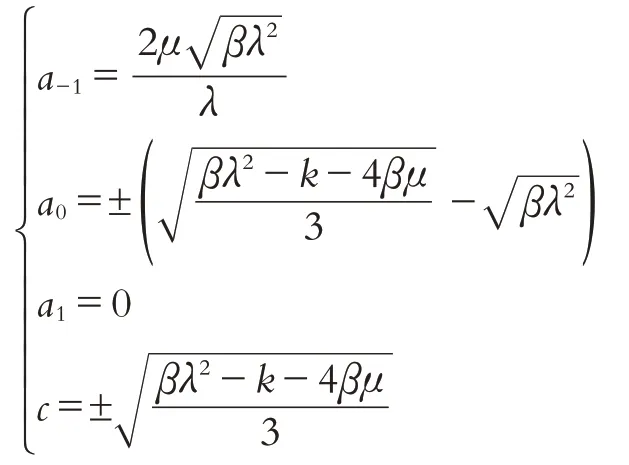
第二组解：

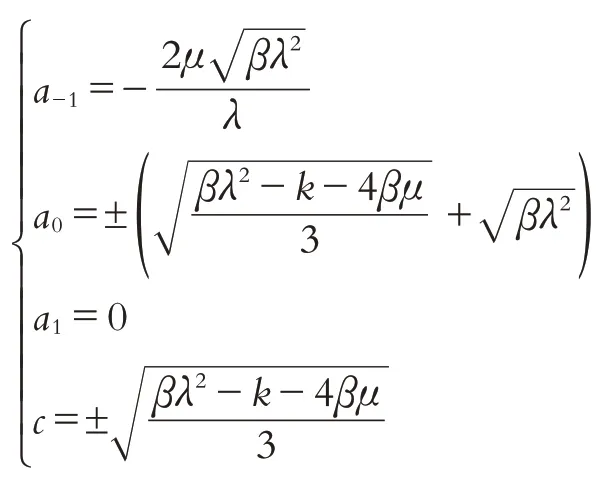
（ⅰ）情形1：λ2-4μ＞0

其中：C1,C2是任意常数.

对应方程（1）的两组双曲函数通解u1(ξ),v1(ξ)与u2(ξ),v2(ξ)分别为：

其中：C1,C2是任意常数.

对应方程（1）的两组三角函数通解u3(ξ),v3(ξ)与u4(ξ),v4(ξ)分别为：

3 总结