刘广 刘济科 吕中荣

(中山大学 航空航天学院 力学系，广东 广州 510275)

在很多复杂科学和新兴领域(如某些具有遗传性和记忆性等全局相关性的领域[1])中，分数阶导数相较于整数阶导数而言有着建模准确、所需参数较少的优势，因此广泛应用于粘弹性材料[2- 3]、机械系统[4- 5]、控制系统[6]和反常扩散[7]等领域。在对这些系统进行建模的过程中，如何准确地确定系统的各种参数一直是一个棘手的问题，尤其是当系统中包含多个分数阶导数算子的时候。确定系统参数的这一类问题可以被归类为参数识别问题，所用的方法即为参数识别方法。

一般来说，参数识别方法可分为两类，其中一类是群智能算法，如遗传算法[8- 9]、人工蜂群体算法[10]等。这些群智能算法的基本思想是模拟自然界生物的群体行为构建随机优化算法，将优化目标转化为个体对环境的适应性，所以具有全局搜索能力和鲁棒性强的优点，且不要求原方程具有严格的连续性和可微性。但是，群智能算法也有一些缺点，比如收敛速度慢、每次计算都会得到不同的结果等。另外一类参数识别方法是基于梯度的方法，如牛顿法[11- 12]和灵敏度法[13]等。在这类方法中，频域或时域的灵敏度法是最常用的，因为它们可以避免求解二阶导数这一繁琐的工作。基于频域的灵敏度法是从大量的由传感器得到的数据去识别系统的固有频率、模态或者其他的系统参数，但是在实际工程中，可以测量到的模态参数总是有限的，而且往往对测量噪声很敏感。与基于频域数据的方法相比，基于时域的灵敏度法具有明显的优势，原则上即使只有一个传感器，只要测量时间足够长，就能获得足够的数据。文中尝试以系统的时域数据来识别分数阶微分系统的参数。

1 分数阶微分方程的正问题求解

考虑如下形式的单自由度线性分数阶系统：

(1)

(2)

式中，β和γ为Newmark-β法的控制参数，Δt为时间步长。文中的分数阶算子Dαx采用Caputo定义，当分数阶阶次0<α<1时，其有以下形式[14]：

(3)

根据Adams离散法则，式(3)可以离散为[15]

(4)

(5)

当1<α<2时，分数阶算子Dαx为以下形式[15]：

(6)

同样，根据Adams离散法则，式(6)可以被离散为

(7)

其中di,n的表达式为

(8)

当0<α<1时，将式(2)和(5)代入式(4)，式(7)变为

(9)

由此可以求得tn时刻的加速度如下：

(10)

式中，

类似地，当1<α<2时，式(7)可以离散为

(11)

则tn时刻的加速度为

(12)

式中，

值得指出的是，上文中的推导也同样适用于线性分数阶多自由度系统，为简便起见文中从略。

2 基于增强响应灵敏度的参数识别

继续选用单自由度系统作为例子来阐述时域灵敏度的分析过程和参数识别过程。考虑式(1)有如下初始条件的情况：

(13)

2.1 分数阶方程的时域灵敏度分析

假设系统(13)中的μ、k和分数阶阶次α都是未知参数，表示为a=(μ,k,α)∈A，其中A是未知参数的可行域。用ai表示a中的第个未知参数。值得注意的是，式(13)中的响应x是未知参数a和时间t的函数，即x=x(t,a)，则x对未知参数的响应灵敏度为

(14)

δ是状态变量x的系数。将式(14)代入式(13)中，灵敏度方程变为

(15)

2.2 反问题

(16)

且R(a)是待识别参数a的函数。我们的目标是从测量数据反过来识别出a=(a1,a2,…,aN)，这样的反问题一般被表述为一个非线性最小二乘优化问题，即找到参数a∈A，使得如下目标函数最小：

(17)

(18)

(19)

(20)

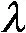
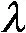
(21)

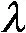
ρcr∈[0.25,0.75]

(22)

(23)

且

(24)

关于式(23)和(24)的详细证明参看文献[16]。由式(15)可知，增大正则化参数可以使迭代更新步长足够小，合理增大正则化参数可以满足置信域限制，此时的正则化也称为增强的正则化。综上，增强响应灵敏度法的算法实现过程如表1所示。

表1 增强响应灵敏度法的算法实现过程Table 1 Flowchart of enhanced response sensitivity approach

3 算例

接下来以一个α=0.5的分数阶自由振动系统和α=1.6的含外激励分数阶系统为例，阐述文中正问题的计算方案和反问题的参数识别过程。表1中增强响应灵敏度法的参数取值分别为tol=10-10，γ=1.414，ρcr=0.5，Nit=1 000，Ntr=20。所有算例选取的测量数据均为加速度响应，倘若考虑测量数据中的噪声，噪声都按照下式进行模拟：

(25)

3.1 0<α<1的分数阶自由振动系统

(26)

可以证明，式(26)有如下形式的解析解[18]：

(27)

在灵敏度分析中，μ和k是方程中某些项的系数，它们的灵敏度解析表达式可以根据式(14)获得且具有如下形式：

(28)

和μ与k不同的是，分数阶阶次α的灵敏度是式(1)中Γ函数的偏微分形式，求解十分繁琐，所以其灵敏度响应用其差分响应代替。假设α有一个摄动量Δ，则系统(26)的摄动系统为

(29)

xα为方程响应，可通过第1节中所述计算格式获得。因此，α的中心差分响应为

(30)

文中所有算例的α的灵敏度都根据式(29)算得。

图1是系统(25)不含噪声的位移响应和加速度响应。可以看出，由第1节中所述的离散格式得到的结果和解析解吻合非常好，图2是含有5%高斯噪声的模拟测量结果。

图1 系统(25)数值解和解析解的响应数据对比

Fig.1 Comparison between analytical and numerical responses of system(25)

图2 系统(25)含5%高斯噪声的测量数据

Fig.2 Measured responses containing 5% Gaussian noise of system(25)

在反问题中，测量数据可以是位移数据或者是加速度数据。假设参数初值为a0=[0.8,1.2,0.5]，测量数据为不含噪声的加速度定义为工况1，对应的无噪声位移响应数据为工况2，测量加速度和测量位移数据含有5%噪声的情况分别定义为工况3和4。图3和4分别是工况1和2中参数的相对误差变化曲线。可以看出，在迭代过程的前10步，参数变化很剧烈，但是大概在20步之后，每次的迭代更新量δa越来越小，识别的结果逐渐逼近真实值。在两个工况中，都是参数α有最大的相对误差，但是两个工况几乎都可以精准地识别出参数的真实值。

图3 工况1中参数的相对误差变化曲线Fig.3 Relative error curves of parameters of Case 1

图4 工况2中参数的相对误差变化曲线Fig.4 Relative error curves of parameters of Case 2

工况3和4的识别结果相较工况1和2来说，精度要低一些,这说明测量噪声的确会造成识别精度的下降。但是无论是工况3还是工况4，其识别的最大相对误差也都在1%以内，所以文中提出的增强响应灵敏度法有着良好的抗噪性。另外还可以看出，文中方法在进行参数识别时，迭代步数都只有几十步，相较于群智能方法而言，计算量大大减少。本算例的详细识别结果如表2所示。

表2 增强响应灵敏度法对分数阶自由振动系统的参数识别结果Table 2 Parameter identification results for fractional-order free vibration system obtained by enhanced response sensitivity approach

3.2 1<α<2的含外激励分数阶系统

不失一般性，接下来考虑一个如下形式的α=1.6的含外激励受迫振动系统：

(31)

和第一个算例不同的是，假设外激励q(t)=sint，同样假设系统中的待识别参数a=[μ,k,α]，其中参数取值为μ=0.6、k=1.5，所以a=[0.6,1.5,1.6]。Newmark-β法中的参数取值和信号采样频率、采样时间等都和3.1节算例相同。根据第1节中所介绍的数值方法，同样可以求得系统(31)的响应。图5所示为系统(31)的位移响应和加速度响应。图6为添加了5%高斯噪声的模拟测量数据。

图5 系统(31)的位移响应和加速度响应Fig.5 Displacement and acceleration responses of system(31)

系统(31)的参数灵敏度方程同样可以按照3.1节算例的方式推导得到，这里不再赘述；α的灵敏度响应根据式(30)以差分响应代替。为测试文中方法对1<α<2分数阶系统的参数识别效果，本算例同样定义4种工况——测量数据为不含噪声的加速度定义为工况1，对应的无噪声位移响应数据为工况2，测量加速度和测量位移数据含有5%噪声的情况分别定义为工况3和4。参数初值设定为a0=[2,2,2]。与算例1类似，本算例中的4种工况都可以准确快速地识别出包括分数阶阶次在内的所有参数，详细识别结果如表3所示。在不考虑测量噪声的情况下，识别结果几乎能够和系统真值相同；在考虑噪声的情况下，也能保持很高的识别精度，同时仅需几十步迭代就可以收敛。

图6 系统(31)含5%高斯噪声的测量数据

Fig.6 Measured responses containing 5% Gaussian noise of system(31)

表3 增强响应灵敏度法对分数阶强迫振动系统的参数识别结果Table 3 Parameter identification results for fractional-order forced system obtained by enhanced response sensitivity approach

4 结语

文中基于Adams离散法则和Newmark-β法，提出了一种针对分数阶系统正问题的求解方案。无论是分数阶阶次α取值为0<α<1还是1<α<2，都给出了相应的离散格式，并用增强响应灵敏度法对分数阶微分系统的参数进行了识别。为了验证所提出的正问题数值方法的有效性，阐述反问题的识别过程，文中还以一个α=0.5的分数阶自由振动系统和α=1.6的含外激励分数阶系统为例进行了说明，得出以下结论：

(1)无论是位移数据还是加速度数据，都可以用于增强响应灵敏度法的参数识别，且加速度数据的识别精度和识别效率都较位移数据要好；

(2)文中提出的识别方法有很强的抗噪性，即便是测量数据中含有5%的噪声，仍旧可以得出很好的识别结果。因此，文中提出的增强响应灵敏度法可以高效准确地识别出分数阶微分系统中的各种参数。将响应灵敏度分析方法推广到更多的非线性领域，将是下一步的主要工作。