摘要：有过程的归纳教学是基于理念、追求事实，是发现知识的教学，本文以《三角形的内角和》一课为例，说明归纳是基于联想的思维形式，让学生进行有知识根据的合乎情理的想象;归纳推理的思维过程是动态的，促进学生经历多种思维沉思的过程，从而归纳概括出一般结论;归纳推理的思维基础是类，通过类来促进学生形成由个别到一般的不完全归纳思维。

关键词：归纳教学;三角形;教学实践

doi：10.16083/j.cnki.1671-1580.2020.03.005

中图分类号： G632                     文献标识码：A                                 文章编号：1671—1580（2020）03—0028—04

三角形一直与人类文化现象密切相关，如金字塔、半坡人面鱼纹彩陶、鼎，其中都不乏三角形的基本结构。人体中存在着不同结构的三角形区域。因此，研究三角形的性质非常有价值。三角形是由边和角两部分组成，本文旨在研究三角形角的特点。

一、有过程归纳教学的价值分析

于伟校长提出“有过程的归纳教学”是强调学生通过不断经历合情合理的推测、探究、体验等操作，不断经历知识原初产生的过程、经历多种形式对话的过程、经历多种思维沉思的过程，从而归纳概括出一般结论的教学。因此有过程地归纳教学是基于理念、追求事实，是发现知识的教学，从而培养学生更为“自然”的思维模式。

（一）内容分析。课标中涉及到三角形的学习有两个“核心词”。第一个是“空间观念”，通过引导学生充分观察、动手操作，并借助想象进一步发展“空间观念”。因此，中年级学生在进行图形与几何领域的学习时，应更多从动手操作中积累认知经验，丰富认知表象，为后继分析图形性质提供感性支撑和直观论据。第二个是“推理能力”，即合情推理与演绎推理。本课渗透的是合情推理中的归纳推理。通过“量”“转”“折”等具体操作探索思路，合情推理用于发现结论，进而再通过演绎推理用于证明结论。 两种推理的有机结合才是完善的推理过程。

（二）价值分析。动手操作可以为学生发现和确定问题的研究方向，但由于操作本身误差的存在，跳出了简单的直观感知层面，避开了“误差尴尬”，凸显出演绎推理的必要性，让数学充满理性色彩。学生就这样通过不断经历合情合理的推测，不断经历知识原初产生的过程、经历多种形式对话的过程、经历多种思维沉思的过程，从而归纳概括出一般结论。因此有过程的归纳教学对《三角形的内角和》的教学具有重要的价值，同时可以培养学生更为自然的思维模式。

二、学情调研与教材分析

（一）学情调研与分析。在有过程的归纳教学中，教师在设计教学时要了解儿童在上课之前持有怎样的生活概念， 有过程归纳教学的就要以儿童这些零散的生活概念为根基， 在此基础上用有趣的、新颖的、富有挑战性的任务来引导孩子系统深刻地再经历知识得出和形成的过程，使儿童低级的生活概念发展为高级的科学概念。

1. 从学生认知起点出发，确定新知的生长点。课前通过调查的方式提出问题： “你对三角形角的特点有哪些了解？ ”结果发现，虽然大部分学生从各种途径知道了三角形的内角和是180度这个结论，但学生不知道为什么所有三角形的内角和都是180度。 所以本节课的教学重点自然就是要让学生经历这个结论的产生过程，而不是结论本身。 同时，我们还要让学生思考这样一个問题，是不是所有的结论都不需要质疑？

2. 紧扣儿童的心理特点，确定新知的学习方式。四年级学生的心理特点是好奇，倾向于直观。 动手操作是这个阶段学生自己能想到且最直接的验证方法，直观且易操作。 学生在研究角的度数问题时，自然想到用量角器量，量一量顺应了学生的原有经验。虽然量角这个操作可以为我们的探究指明方向， 但因为操作有误差，学生自然会思考： 得到结论的方法本身是否严谨？ 为引出更科学、更严谨的验证方法提供铺垫。因此，更严谨的演绎推理的学习方式也应该是该课的重点之一。

（二）不同版本教材对比与分析。对比国内现行几个版本教材，笔者发现其中人教版、北师版、青岛版和苏教版这四个版本教材对于该内容的引出方式都是大致相似的，都是通过动手操作，即用画、量、算等符合儿童认知特点的方法进行引入，经历对不同种类三角形的三个内角测量、计算的过程，让学生初步感悟结论。教材的这种编排尊重学生学习特点的同时，遵循了图形认识的内在规律。不同的是苏教版测量的是学生手边比较熟悉的两个三角板。青岛版版本教材既强调了操作证明的实际意义，同时也通过折一折的活动渗透了平行公理。

浙教版教材的引入方式最为与众不同，其他版本教材都是从测量入手，只不过有的量的是自己制作的三角形，有的量的是现成的三角板。而浙教版教材有着探究学习的意味，它是从变化的三角形入手，让学生猜测变化的三角形背后隐藏着什么不变的东西，从而得到一个假设三角形内角和是一个固定的读数，是不变的东西。最后再通过验证并得到结论三角形的三个内角和是180度。

通过以上分析，不难发现大多数教材都是从实践操作入手探索三角形的内角和，通过合情推理得到结论，但没有—个版本的教材从演绎证明的角度来探索与研究三角形内角和。

三、学习材料的选择与任务设计

通过学情分析和不同版本教材的对比分析，我们确定利用合情推理和演绎推理相结合来进行三角形内角和的学习。

首先我们通过“量”“算”“折”等具体的操作层层推进，让学生深刻感受变化的三角形蕴含着不变的东西，即三角形的内角和是一个固定的度数。也就是基于有过程归纳，利用合情推理（实验操作）来探索思路，发现结论。

其次利用长方形和正方形的内角和来证明直角三角形的内角和就是180度，最后把锐角三角形和钝角三角形转化成直角三角形来证明，从而得出结论“任意三角形的内角和都是180度”。当然，由于最后锐角三角形和钝角三角形的证明对于四年级的学生来说相对比较难，所以本节课的演绎推理重点证明“直角三角形内角和是180度”的结论，关于锐角三角形和钝角三角形的内容作为拓展内容来学习。

四、有过程归纳教学的展开

（一）归纳是基于联想的思维形式，让学生进行有知识根据的合乎情理的想象。让学生学会联想是让学生知道并学会归纳最基本的思维方法。这种在有知识基础的和有知识根据的合乎情理基础上的设想，使学生能借助已知产生“正迁移”引发联想，为推理提供良好的学习氛围。借助直观图形“变化的三角形”，引发猜想三角形的内角和是否是一个确定的度数，如果是一个确定的度数可能是多少，激发了学生验证的兴趣，为接下来合情推理做了铺垫。

师：上节课我们根据一定的标准把所有的三角形都进行了分类，（出示大屏幕）这节课我们要来细致地研究三角形（板书：三角形），你觉得可以研究它的什么？（角）

师：老师这里有一个可以变化的三角形，请你仔细观察在三角形变化的过程中，它的三个角有什么变化？（有的角在变大，有的角在变小）这能说明什么？

生：三角形的内角和是180度。

师：用眼睛就能看出是180度？那我们能确定什么？

生：内角和是一个固定的度数，

师：看来内角和可能真是固定的，刚才有同学说是多少来着？（板书：180度）有没有什么问题要问他？（教师用剪刀剪一个小三角形）这个大的和这个小的也一样？（板书：大小不同）那这两个形状不同的呢？（板书：形状不同）

师：数学学习要严谨，要有理有据，到底是不是你们说的180度，得怎么办？

（二）归纳推理的思维过程是动态的，促进学生经历多种思维沉思的过程，从而归纳概括出一般结论。归纳推理的思维过程是动态的，既有直观的实验感知，又有理性的数学思考。分析、比较是归纳的基本思维形式。动手操作一定要与分析、比较等思维活动结合起来，跳出简单的直观感知层面，涉及逻辑推理论证层面。通过不断经历合情合理的推测，经历形象与抽象等多种思维沉思的过程，从而归纳概括出一般结论。

师：先看学习要求。想一想你要用什么方法得到三角形的内角和？想好了吗？有没有想用量角器测量的举手，老师对你们有一个要求，三个角的数据必须是实际量出来的，只要量完就不许再改了，把你量完的数据直接用水彩笔写在每个角的旁边。如果你用的是其他方法，把你的作品贴在学习卡1上。

师：我看到同学们都得到了自己手里三角形的内角和，接下来我们来分享自己的方法，因为每个同学手里的三角形不一样，用的方法也可能不一样，所以倾听的时候不懂就问，有疑问就质疑补充，交流结束之后完善自己的方法，一会带着自己的作品以个人的形式进行汇报。

学生汇报不同方法。

1.量。师：他量的锐角三角形，谁量的不是这样的三角形？还有量的不是黑板上这两种的吗？老师调查一下，选择测量方法的同学，你们量完之后发现问题了吗？为什么会这样呢？如果给你的三角形非常标准，你能保证逐个量完加在一起就一定是180度吗？为什么不能？因为测量有误差。

师：通过测量我们能确定什么？（板书： 180度左右）谁还有不同方法？

2.拼

（1）撕拼。师：明明是三个内角到这里，转化成一个角了。（板书：转化）看起来和平角很接近，那是不是一定是平角呢？平角有什么特点？看来只要是操作就一定有误差。現在我们可以进一步确定三角形的内角和确实和180度很接近。（板书：接近180度）

（2）折拼。师：这个方法和前面的哪个方法是一回事？折的时候需要有一定的技巧和要求。

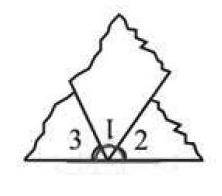
（3）多个三角形拼。师：老师这里也有个拼的方法，猜猜是谁的方法？古代有位数学家泰勒斯，他受到拼图方法的启发，把六个完全一样的三角形拼在了一起，从而得到了三角形的内角和。有看懂的吗？

生：这里有两个角1，两个角2，两个3。三角形内角和也就是360÷2=180度。

师：但是在拼的过程中三角形和三角形之间是有缝隙的，因此泰勒斯也无法确定三角形的内角和就一定是180度，但他为后来数学家的研究指明了方向，三角形的内角和很可能就是180度。

3.证明。师：同样我们刚才的研究也为接下来的学习指明了方向，就着这个方向，接下来我们来思考，能不能借助哪种我们已经知道内角和的图形来证明三角形的内角和就是180度呢？

（1）直角三角形。师：这里有个提示，可以在学习卡画一画，老师给每个小组准备了一个信封，里面有直角三角形，可以拿出两个完全相同的直角三角形先标上角再摆一摆。

生独立学习并汇报。

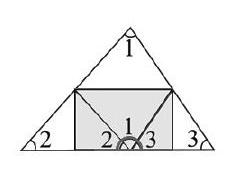
师：有疑问吗？那这两个直角三角形的内角一共是6个内角，这6个内角跟长方形的4个内角有什么关系？怎么能确定其中一个直角三角形的内角和就是长方形一半的呢？

师：我们根据长方形的内角和推理计算出任意直角三角形的内角和。（板书：计算推理）这个直角三角形的内角和是180度，其他直角三角形呢？

（2）锐角、钝角三角形。师：锐角三角形、钝角三角形怎么说明它们的内角和？能不能借助已经知道的直角三角形的内角和来推算出来呢？同桌两人研究一种图形，另外两个同学研究另一种。

师：老师看很多同学遇到了困难，可以抬头看看大屏幕上老师给的提示。谁看懂了？

生：锐角三角形通过作高，其实可以看成两个直角三角形的内角和减去合并在一起的两个直角，所以锐角三角形的內角和是180度。钝角三角形也是一样的道理。

师：我们也证明出了锐角三角形和钝角三角形的内角和。现在可以得到什么结论？

生：我们研究三角形的内角和都是180度。

（三）归纳推理的思维基础是类，通过类来促进学生形成由个别到一般的不完全归纳思维。由于完全归纳推理具有局限性和不可实现性，尤其是需要归纳推理的数量过于庞大，如果遵循完全归纳推理原则，就需要调查所有的三角形，这是一种不实际的推理原则。不完全归纳是相对完全归纳而言，不完全归纳推理是统计推理归纳中比较常用的一种方法，在集合中有每个类中具有代表性的元素，从而归纳概括出一般结论的同时，形成由个别到一般的归纳思维。

师：说说我们到目前为止得到的研究结论吧。不对呀，我们才研究不到40个吧，怎么能直接说三角形都是这样呢？需不需要把世界上所有的三角形都拿来一一研究呢？

生：把这三类三角形分别研究一些，就可以代表所有三角形了。

师：我们由30多个个别的三角形来推出一般的所有三角形的内角和很可能就是180度，这个过程在数学上被称为归纳推理，这是我们在数学学习中经常用到的方法。（板书：归纳推理）

[参考文献]

[1]于伟.教育哲学[M].北京：北京师范大学出版社，2015.

[2]于伟.与儿童的对话：儿童哲学研究的田野笔记[M].长春：长春出版社，2017.

[3]于伟等著.率性教育的理论与实践探索[M].北京：教育科学出版社，2018.

[4]皮亚杰.尚新建等，译.生物学与认识[M].北京：生活·读书·新知三联书店，1992.

[5]史宁中.《数学课程标准》的若干思考[J].数学通报，2007（05）.

[6]于伟.“率性教育”：建构与探索[J].教育研究，2017（05）.

Promote Students Thinking Development based on Process Induction

——Taking the Sum of the Inner Angles of a Triangle as an Example

SUN   Yanjun

（Primary school affiliated to Northeast norma I university， Changchun  Jilin 130000， China）

Abstract： A process of inductive teaching is based on the concept， the pursuit of truth， is to discover knowledgeteaching. This paper takes the sum of the inner angles of atriangleas an example to illustrate that induction is a thinking formbased on association， so that students can have reasonable imaginationbased on know ledge. The thinking process of inductive reasoning isdynamio， which promotes students to exper ience the process of thinkingmeditation， thus generalizes the general conclusion. The thinking basis ofinductive reasoning is class， which can promote students to formincomplete inductive thinking from individual to general.

Key words： process induction; teaching induction; triangle

[责任编辑：王 辰]

收稿日期：2020—01—05

作者简介：孙艳君（1984—），女，江苏徐州人，东北师范大学附属小学教师，小学高级教师，硕士。吉林省小学数学骨干教师，2019年省培计划省骨干培训班学员。研究方向：数学教育。