张华夏

(中山大学 哲学系，广东 广州 510275)

一、从标准分析看哲学上的运动论题和黑格尔的辩证法

(一)关于辩证法所说的“时点”与“地点”

(二)关于极限定义的本质

(三)关于无理数、“死去了的量的鬼魂”和改进辩证法问题

就此公式而言，贝克莱根本抓不到什么把柄。这里 dy/dx根本不是陈文所说的除数与被除数；而Δx是个变量，本身不是0，它的极限值是0，这里根本不出现陈晓平所说的“Δx既是0又不是0”[1]6的矛盾。而且，这里根本不是变量与常量的关系问题。不管Δx的极限值是什么，Δx和它的函数Δy都是变量，它们都有定义域，这个定义域是由一定的实数常量域组成，不要认为，只要Δx是个变量就万事大吉了，就可以说明运动“在这一点又不在这一点”(初步辩护)，并且还说明“运动‘在这一点又不在这一点’本身不是矛盾的”(改进辩证法的表达方式的终极辩护)。陈晓平在论文摘要中一再提出这几个问题，向当代的微积分的常识进攻，使人感到有点故弄玄虚。不过他的积极意义要到我们讨论非标准分析微积分的时候才能展露出来。

(四)关于黑格尔和恩格斯所讲到的机械位移的矛盾

陈晓平对“此时”、“此刻”(“now”或“instant”)给出了一个意指“无穷小区间”的意思。前面笔者提问过，他们在哪里说过“此无穷小区间”和“彼无穷小时刻”的话？其实黑格尔和恩格斯对于陈文强加给他们的话并不领情，因为他们讲的是矛盾辩证法，指的是运动在此时此刻在这一点又不在这一点，并声明这是违反形式逻辑的。这是矛盾辩证法的常识之一。

二、从非标准分析来看哲学上的运动论题和黑格尔的辩证法

(一)历史

图1 牛顿求切线的微分法

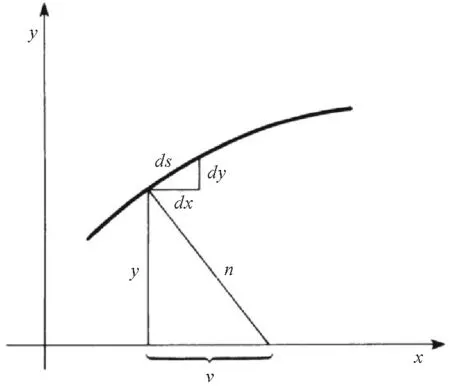
图2 莱布尼茨求导数的微分法

这里ds/n=dx/y或yds=ndx。这些无穷小的总和便得到[5]：

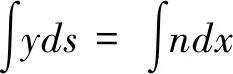
不过莱布尼茨还没有建立一个系统的实无穷小理论，从认识论上看，他将它看作是一种有很好基础的“虚构”，像虚数一样，它是有用的，并服从通常数的规律。但从本体论上看，他更多地将无穷小看作是万物由此组成的不可再分的最小的原子，无穷小是小于一切甚至小于任何实数的实无穷小[4]2,7。非标准分析(9)关于非标准分析的一些参考文献：鲁滨逊.非标准分析[M].申又枨,王世强,张锦文,等译.北京:科学出版社,1980; KEISLER H J.Elementary calculus: An infinitesimal approach[M].Long Island:Courier Corporation,2013; SALBANY S, TODOROV T.Nonstandard analysis in point-set topology[M].Vienna:Preprint ESI 666,1999.继承莱布尼茨的理论，承认实无穷小。提出了超实数的概念，它包含了实数作为它的子集，用各种各样的无穷小扩展了实数。

(二)什么是非标准分析

20世纪60年代初，德国数学家亚伯拉罕·鲁滨逊(Abraham Robinson)提出非标准分析，重新回到莱布尼茨的实无限进路，并以此为数学分析建构出一个严谨的基础(10)鲁滨逊的《非标准分析》(ROBINSON A.Non-standard analysis[M].Amsterdam:North-Holland Publishing Company,1966)一书发表于1966年，书中的某些主题已出现于其1961年的同名文章(ROBINSON A.Non-standard analysis[J].Proceedings of the Royal Society A,1961,64:432-440)中。参见：Non-standard analysis[EB/OL].(2019-03-27)[2019-04-01].https://en.wikipedia.org/w/index.php?title=Non-standard_analysis&oldid=889717193:5.Robinson’s book; ROBINSON A.Introduction to model theory and to the metamathematics of algebra[M].Amsterdam:North-Holland Publishing Company,1963:278.。数学家与逻辑学家哥德尔(Kurt Gödel)说：“不论从哪方面看，非标准分析将会成为未来的数学分析……在实数之后，下一个十分自然的步骤，即引入无限小竟被轻易地忽略了……它在发明微积分后300年才发展起来，这是数学史上的一件大怪事。”[6]

1.定义与组成

超实数域*R是将实数域R作为它的子集的一个系统。其中的实无穷小数x用δ，ε来表示，这与标准分析对它们的用法不同，如果对于所有的正实数r，有|x|r。实数和超实数都是有序(ordered sequences)的，例如可以由小到大(或由大到小)排个队。这些都是实数与超实数的共同性质。在这方面，它们是同构的。这个组成可以用下面的超实数组成图表示。(见图3)

图3 超实数组成图[7]

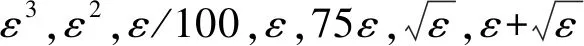
2.运算法则

非标准分析认为在任何两个实数之间有许多(前面讲过是无限多个)无穷小存在。至少有这样的法则：无穷小×有限量=无穷小，无穷小+无穷小=无穷小，[8]很可能还有一个公式：无穷小×无穷大=有限数。莱布尼茨正是以这个公式求得圆的面积和曲线的周长(12)莱布尼茨的学生洛必达在《无限小分析》(L′HPITAL G D.Analyse des Infiniment Petits pour l′Intelligence des Lignes Courbes[M].Paris:Imprimerie royale,1696.)以公理的形式写道：“第二公理：曲线是由无穷多个长度为无限小量的直线组成”。参见：张锦文.无限小量方法与非标准分析[J].曲阜师院学报(自然科学版),1979(1):1-7.。鲁滨逊说*R除了它是非阿基米德域这一点外，其他性质与R相同，稠密性、有序性等等在*R中同R一样，能进行加、减、乘、除等运算[9]。实数数学中的结合律、交换律、分配律、同一律、传递律在超实数中都成立。而最基本的与实数域同构的运算法则可以用公式简要表示为：*R= (*R ,+, •，<) 这里*R为超实数有序域，*R为超实数；它们同构于实数域R= (R，+, •，<)。

根据非标准分析，如果x，y∈*R，并且x-y是无穷小，则称x与y彼此无限逼近，记作x≈y；如果x，y是有限的超实数，则x≈y≈r，r为唯一实数。我们称r为x，y的标准部分，记作：r=st(x) 和r=st(y),即st(x)=st(y) 。独立变量的导数的定义就是df(x)/dx=st((f(x+Δx)-f(x))/Δx)，这里实无穷小Δx≈0。

图4 积分图

(三)非标准分析对标准分析的批评

关于连续性，从标准分析的观点看，在数轴上，实数不但是稠密的、有序的，而且是连续的。因为实数在进到一点之后，无下一点可言，所有的点都是连起来的。可是从非标准分析的观点看，在任何两个标准点之间有无数的实无穷小，这就打破了标准分析及其运动概念的连续性。因为从非标准分析的观点看，数轴上的点的长度就只是0，线段如果是点的集合，那么数轴上无限个0的集合也只能是0。与此相反，实无穷小无论怎样小，超实数数轴都是离散的，在数轴上总有一个不能忽略的长度，正是它足够将数轴填满，我们说过它被假定有无限个长度点，这岂不是芝诺对了，这里有数不完的空间点要数。但是，在数空间点的数量的有限时间里也有数不完的时间点。我们在非标准分析的运算法则中创立了一个公式：“无穷小×无穷大=有限数”，这等于说“无穷大÷无穷大=有限数”。这意味着阿基里斯能够在足够的时间里走过有限的实数距离。如果实无穷小意味着它在数轴上有连续性，运动便可以连续走过去。无论怎么说，芝诺第一悖论的“阿基里斯赶不上龟”不能成立：阿基里斯可以赶上龟。[10]

关于黑格尔的矛盾运动观念，陈文从标准分析的极限论出发，认为只要有一个无穷小变量的观念，在此种变量观念下，“在这一点又不在这一点”便很好解释(初步辩护)并且又不违反形式逻辑。殊不知黑格尔和恩格斯讲矛盾运动时从来就是指“既是(在这一点)又不是(在这一点)”，他们在该意义下明确地说了这是违反形式逻辑的。相反，非标准分析讲的运动从来就是符合(形式)逻辑的，而且它的建立首先从逻辑上得到很好的论证。在这里，黑格尔没有得到任何便宜，他也不想得到这个便宜。

(四)非标准分析与芝诺悖论

从非标准分析的观点看，芝诺悖论(13)关于非标准分析与芝诺悖论的一些参考文献：SALMON W C.Space, time and motion[M].Minneapolis:University of Minnesota Press,1980; DOWDEN B. Zeno’s paradoxes[EB/OL].[2019-04-01].https://www.iep.utm.edu/zeno-par/；MCLAUGHLIN W I.Resolving Zeno’s paradoxes[J].Scientific American,1994,271(5):84-89；MCLAUGHLIN W I, MILLER S L.An epistemological use of nonstandard analysis to answer Zeno’s objections against motion[J].Synthese,1992,92(3):371-384；PAPA-GRIMALDI A.Why mathematical solutions of Zeno’s paradoxes miss the point: Zeno’s one and many relation and Parmenides’prohibition[J].The Review of Metaphysics,1996,50(2):299-314； Zeno’s paradoxes[EB/OL].(2019-02-20)[2019-04-01].https://en.wikipedia.org/w/index.php?title=Zeno%27s_paradoxes&oldid=884310256.主要是三个问题：阿基里斯赶不上龟，一分为二永远数不完和飞矢不动。无论实无穷小是多么短的线段，不论乌龟走得多远，一分为二分得多细，都可以将它数完(或量度完)。这样，芝诺悖论的问题便集中在“飞矢不动”上。从“飞矢不动”看，在每一个时刻点上，飞矢的确是不动的。无论标准分析还是非标准分析都是如此。必须在一个区间里，例如(a，b)里，才能说它从a点运动到b点。这就是罗素的at-at理论。(“运动的at此时-at此地的理论”)这个观点首先是亚里士多德提出来的。这又是关系到一个长度是怎样被形成、是怎样被经过的问题，它首先要求有一个时间段落，对应着它才有一个被决定的空间段落，如果速度等于零，它还是不动的。罗素的意见是，运动是位置对于时间的函数，无论标准分析还是非标准分析情况都是这样。按照这个意见，黑格尔没有得到任何便宜：从非标准分析的观点看，在数轴上当t进到实数划分的t1处时，s只能够按照s=f(t) 在s1处，不能同时在s2处(这里s1≠s2)。而在数轴上，当t进到超实数划分的t1+ε1处时，按照*s=f(t+ε)，它只能在f(t1+ε1)处，不能也在另一个地方，例如f(t1+ε2)处。这里ε1与ε2都是实无穷小，它们不定义在自然数和实数上。而是在实数之外进行定义，黑格尔自我欣赏的在这里又不在这里的自相矛盾是错误的。非标准分析没有这个错误。

事实上，用戴德金分割来解决芝诺悖论只是一个权宜之计，因为它先要有一个前提。戴德金分割解决了实数是有理数与无理数的集合这一问题，这是该进路的贡献，但是没能触及到“数轴是点的集合”这一前提。对此，我们可以从超实数的研究得到一些启示。我们的进路不但要从数学模型的观点来分析运动，而且要从物理学的观点分析运动，这时运动的物体是有长度的，夸克也是有长度的，从这个观点看，芝诺悖论是很容易驳倒的。不过这是非标准分析微积分，它是未来的微积分，现在，柯西的微积分占了主导地位。用非标准分析来讲授微积分，目前在美国的大学里也只是试验性的。本文也只是以非标准分析解决芝诺悖论与辩证法运动论题的初步尝试，望能抛砖引玉，引起学界对此研究进路的重视。