胡献国, 吕家凤

(浙江师范大学 数学与计算机科学学院,浙江 金华 321004)

0 引 言

1933年,Ore[1]介绍了一类非交换的多项式环,这已经成为环理论中的最常用的一种构造,常称之为Ore扩张.2006年,文献[2]引入了Poisson多项式代数,自此,Poisson Ore扩张的方法被广泛使用.例如，近来文献[3]讨论了Poisson Hopf代数的Poisson Ore扩张的Hopf结构,并从泛包络代数的角度对Poisson Ore扩张展开了详细的研究[4].2008 年,文献[5]发展了Ore扩张的理论,给出了二重Ore扩张的概念,并通过二重Ore扩张构造了几类整体维数为4的Artin-Schelter正则代数[6].2011年,文献[7]讨论了二重Ore扩张与迭代Ore扩张之间的关系;2018 年,文献[8]给出了二重Poisson Ore扩张的泛包络代数的具体结构.受以上结果的启发,本文主要考虑Poisson Hopf代数在二重Poisson Ore扩张下的代数结构,给出了Poisson Hopf代数的二重Poisson Ore扩张仍为Poisson Hopf代数的等价条件.

本文如无特别说明,所有的代数都含有单位元1,k表示特征为0的基域,所有的代数、余代数、Hopf代数与张量积都在k上.

1 二重Poisson Hopf扩张

首先介绍Poisson Hopf代数、二重Poisson Ore扩张、二重Poisson Hopf扩张等相关概念和基本性质.

余代数与Hopf 代数的定义及相关性质可参阅文献[9].与余代数相关的记号如下：对于余代数C,分别用Δ与ε表示余乘法与余单位；对于任给的c∈C,根据Sweedler记号,记Δ(c)=Σ(c)c(1)⊗c(2)，在具体的使用中,Σ(c)经常省略不写；令G(C)为C中所有类群元的集合,C+为余单位ε的核.

设(A,{·,·}A)与(B,{·,·}B)均为Poisson代数[10],若存在代数同态f:A→B,使得对任给的a,b∈A,有f({a,b}A)={f(b),f(a)}B,则称f为Poisson代数反同态.另一方面,对于任给的交换代数A,令[a,b]=ab-ba,∀a,b∈A.易证(A,[·,·]) 是Poisson代数.

定义1[10]设Poisson代数(A,{·,·})是k上的双代数(A,m,μ,ε,Δ),其中m:A⊗A→A和μ:k→A分别表示代数A的乘法与单位.如果对任给的a,b∈A,有Δ({a,b})={Δ(a),Δ(b)}A⊗A,那么称A为Poisson双代数.若在此基础上,A还是Hopf代数,则称A为Poisson Hopf代数.

例1设A=k[g±1,y1,y2],则在A上存在唯一的Hopf结构,使得Δ(g)=g⊗g与Δ(yi)=g⊗yi+yi⊗1,其中i=1,2,g∈G(A).易知,A上的对极为S(g)=g-1与S(yi)=-g-1yi,i=1,2.更进一步,如果令

{y1,g}=-λgy1, {y2,g}=λgy2, {y2,y1}=λy1y2,λ∈k,

那么A是Poisson Hopf代数.

对于Poisson Hopf代数,有下面结果[3]:

命题1设A为Poisson Hopf代数,那么对任给的a,b∈A,有:

1)ε({a,b})=0;

2)S为Poisson代数反同态,即

S(ab)=S(a)S(b);S({a,b})={S(b),S(a)}.

在文献[8]中,二重Poisson Ore扩张是由左二重Ore扩张的semiclassical limit来定义的，其定义如下:

设R是Poissonk-代数,R[y1,y2]是交换多项式环.令

其中,M2×1(R),M2×2(R)与M2×1(R[y1,y2])均为PoissonR-模[8].

由文献[8]可知,当Poisson括号{·,·}满足

(1)

时,R[y1,y2]是Poisson代数.更进一步，对任给的a,b∈R,式(1)成立当且仅当{q,α,ν,ω}(常称之为PDE-数据)满足下列关系：

1)α(ab)=aα(b)+bα(a); 2)ν(ab)=aν(b)+bν(a);

3)α({a,b})={α(a),b}+{a,α(b)}+[α(a),α(b)];

4)ν({a,b})={ν(a),b}+{a,ν(b)}+α(a)ν(b)-α(b)ν(a);

5){y2,{y1,a}}+{y1,{a,y2}}+{a,{y2,y1}}=0.

其中,[α(a),α(b)]=α(a)α(b)-α(b)α(a).

Poisson结构满足式(1)的 Poisson代数R[y1,y2]被称为R的二重Poisson Ore扩张,或简称为R的二重Poisson扩张,记为R[y1,y2;α,ν]p.此时,称{q,α,ν,ω}为二重Poisson扩张的PDE-数据.

受文献[3,11]的启发,可给出如下的定义:

定义2设R是Poisson Hopf代数,R[y1,y2;α,ν]p是R的二重Poisson Ore扩张.若R[y1,y2;α,ν]p是Poisson Hopf代数,使得R是其Poisson Hopf子代数,则称R[y1,y2;α,ν]p是R的二重Poisson Hopf扩张.

相应地,可以给出迭代二重Poisson Hopf扩张的定义.

定义3设R是Poisson Hopf代数.若B是Poisson Hopf代数,且B包含如下的Poisson Hopf子代数链:

R=B(0)⊂…⊂B(i)⊂B(i+1)⊂…⊂B(n)=B,

使得每个扩张B(i)⊂B(i+1)=B(i)[yi+1,yi+2;αi+1,νi+1]p均为二重Poisson Hopf扩张,则称B是R的迭代二重Poisson Hopf扩张.

2 二重Poisson Hopf扩张的等价条件

下面将给出Poisson Hopf代数R的二重Poisson Hopf扩张的等价条件.

从现在起,假定R为Poisson Hopf代数,A=R[y1,y2;α,ν]p是R的二重Poisson扩张,I是恒等映射R→R.令Δ(yi)具备如下形式:

Δ(yi)=gi⊗yi+yi⊗1+ui.

(2)

式(2)中:ui∈R⊗R;gi是R中的类群元;i=1,2.进一步,假设ε(yi)=0,ui=∑uui1⊗ui2∈R+⊗R+.在使用过程中,∑u也经常省略不写.为方便起见,将式(2)简记为

Δ(y)=g⊗y+y⊗1+u.

若A为Poisson Hopf代数,则由余结合性与对极公理可推出如下等式:

命题2若A是R的二重Poisson Hopf扩张,则有下述等式成立:

1)Δα(a)=α(a(1))⊗a(2);

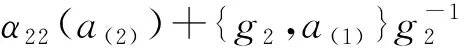
3)Δα(a)·u+Δν(a)=ga(1)⊗ν(a(2))+ν(a(1))⊗a(2)+{u,a(1)⊗a(2)}.

证明 由式(1)所定义的Poisson关系可推出

{Δ(yi),Δ(a)}=Δ({yi,a})=Δαi1(a)Δ(y1)+Δαi2(a)Δ(y2)+Δνi(a).

其中,a∈R.注意到

{Δ(yi),Δ(a)}={gi⊗yi+yi⊗1+ui,a(1)⊗a(2)}=gia(1)⊗(αi1(a(2))y1+αi2(a(2))y2+νi(a(2)))+

{gi,a(1)}⊗a(2)yi+(αi1(a(1))y1+αi2(a(1))y2+νi(a(1)))⊗a(2)+{ui,a(1)⊗a(2)}.

而

Δαi1(a)Δ(y1)+Δαi2(a)Δ(y2)+Δνi(a)=

Δαi1(a)(g1⊗y1+y1⊗1+u1)+Δαi2(a)(g2⊗y2+y2⊗1+u2)+Δνi(a).

当i=1时,分别比较1⊗y1,y1⊗1,1⊗y2,y2⊗1与常数项的系数,可得:

Δα11(a)u1+Δα12(a)u2+Δν1(a)=g1a(1)⊗ν1(a(2))+ν1(a(1))⊗a(2)+{u1,a(1)⊗a(2)}.

当i=2时,有相应的式子成立.因此,命题2得证.

命题3采用上面的记号,则有下列陈述成立:

1)存在线性映射η:R→M2×2(k),使得对任给的a∈A,有

2)η:R→M2×2(k) 满足下列关系:

η(ab)=ε(a)η(b)+ε(b)η(a);η({a,b})=0.

其中,a,b∈A.

证明 1)令η(a)=α(a(1))S(a(2)),其中a∈A.由命题2可得

Δη(a)=Δα(a(1))ΔS(a(2))=(α(a(1))⊗a(2))T(S⊗S)Δ(a(3))=

α(a(1))S(a(4))⊗a(2)S(a(3))=α(a(1))S(a(3))⊗ε(a(2))=η(a)⊗1.

其中,T(a⊗b)=b⊗a,∀a,b∈A.因此,对任给的a∈A,η(a)可看成是一个标量,故可将η看成是从R到M2×2(k)的线性映射.

更进一步,有

α(a)=η(a(1))a(2).

(3)

将式(3)代入命题2的2),并在两边同时作用I⊗ε,可得

2)由于α满足PDE-数据中的第1)和第3)条关系,因此对任给的a,b∈A,有

η(ab)=α((ab)(1))S((ab)(2))=α(a(1)b(1))S(a(2)b(2))=

(a(1)α(b(1))+b(1)α(a(1)))S(b(2))S(a(2))=ε(a)η(b)+ε(b)η(a).

注意到

α({a,b})=η(a(1)b(1)){a(2),b(2)}+η({a(1),b(1)})a(2)b(2)=

(ε(a(1))η(b(1))+ε(b(1))η(a(1))){a(2),b(2)}+η({a(1),b(1)})a(2)b(2)=

{a,α(b)}+{α(a),b}+η({a(1),b(1)})a(2)b(2),

与PDE-数据中的第3)条关系相对比,有

[α(a),α(b)]=η({a(1),b(1)})a(2)b(2).

(4)

在式(4)两边同时作用ε,可得

ε([α(a),α(b)])=ε(η({a(1),b(1)})a(2)b(2))=η({a,b}).

注意到R为Poisson Hopf代数,由命题1可得,η({a,b})=0.命题3得证.

命题4若A是R的二重Poisson Hopf扩张,并仍采用上面的记号,则有下列等式成立：

(q11u1+q12u2)u1+Δ(ω1)u1+Δ(ω2)u2+Δ(ω0).

证明 由式(1)所定义的Poisson关系可推出

注意到

{Δ(y2),Δ(y1)}={g2,g1}⊗y2y1+g2g1⊗{y2,y1}+{g2,y1}⊗y2+{g2⊗y2,u1}+{u2,u1}+

{y2,y1}⊗1+{y2⊗1,u1}+{u2,g1⊗y1}+{u2,y1⊗1}+{y2,g1}⊗y1=

ν1(g2))⊗y2+{u2,g1⊗y1}+(α21(g1)y1+α22(g1)y2+ν2(g1))⊗y1+{u2,u1}=

(α22(g1)⊗1)(y2⊗y1)-(α12(g2)⊗1)(y2⊗y2)+(ν2(g1)⊗1+{u21,g1}⊗u22+

g2u11⊗α21(u12))(1⊗y1)+(-g1u21⊗α11(u22)+g2g1⊗ω1)(1⊗y1)+

(α21(g1)⊗1)(y1⊗y1)+(-ν1(g2)⊗1-{u11,g2}⊗u12+g2u11⊗α22(u12))(1⊗y2)+

(-g1u21⊗α12(u22)+g2g1⊗ω2)(1⊗y2)-ν1(u21)⊗u22+

[ω1⊗1+α21(u11)⊗u12-α11(u21)⊗u22](y1⊗1)+ν2(u11)⊗u12+

[ω2⊗1+α22(u11)⊗u12-α12(u21)⊗u22](y2⊗1)+g2u11⊗ν2(u12)+

ω0⊗1+g2g1⊗ω0+{u2,u1}-g1u21⊗ν1(u22).

另一方面

q11(g1⊗y1+y1⊗1+u1)(g1⊗y1+y1⊗1+u1)+Δ(ω0)+q12(g1⊗y1+y1⊗1+u1)(g2⊗y2+y2⊗1+u2)=

q12(g1⊗1)(y2⊗y1)+2q11(g1⊗1)(y1⊗y1)+(q12u1+Δ(ω2))(y2⊗1)+

(2q11u1+q12u2+Δ(ω1))(g1⊗1)(1⊗y1)+Δ(ω2)u2+Δ(ω1)u1+

(q12u1+Δ(ω2))(g2⊗1)(1⊗y2)+(q11u1+q12u2)u1+Δ(ω0)+(2q11u1+q12u2+Δ(ω1))(y1⊗1).

综上所述,有如下定理成立,该定理可看成是文献[11]定理2.4的Poisson Hopf情形.

1)存在线性映射η:R→M2×2(k),使得对任给的a∈R,有

(5)

而且该映射η满足如下条件:

η(ab)=ε(a)η(b)+ε(b)η(a);η({a,b})=ε([α(a),α(b)])=0, ∀a,b∈R.

(6)

u⊗1+(Δ⊗I)(u)=g⊗u+(I⊗Δ)(u);

(7)

(8)

3)映射ν满足:Δν(a)-ν(a(1))⊗a(2)-ga(1)⊗ν(a(2))={u,Δ(a)}-Δα(a)·u.

4)所有的这些数据还需满足命题4中的1)～5)5个等式.

注意到:式(6)中的条件η(ab)=ε(a)η(b)+ε(b)η(a)说明η:R→M2×2(k)是一个代数导子.类似证明定理1的逆命题仍是正确的,即

例2采用例1中的记号,则A=k[g±1,y1,y2]是Poisson Hopf代数.令R=k[g±1],则R为A的Poisson Hopf子代数,其Poisson括号具有平凡的Poisson结构.易证A是R的二重Poisson Hopf扩张,其对应的PDE-数据为{q,α,ν,ω}.其中:

注1很显然,例2中的Poisson Hopf代数R=k[g±1]还可以实现迭代二重Poisson Hopf扩张.

3 结 语

给出了Poisson Hopf 代数的二重Poisson Hopf扩张的等价条件.这个结果推广了文献[3]的Poisson Hopf扩张的等价条件.由于本文所讨论的Hopf代数结构并没有具备一般情形,接下来可以考虑下面的问题:对于任给的Hopf代数结构,是否也能给出二重Poisson Hopf扩张的等价条件?为此,笔者将进行更深层的研究.