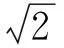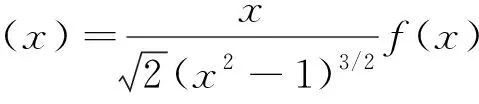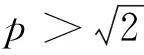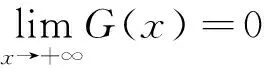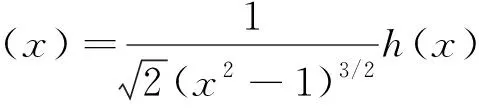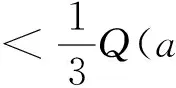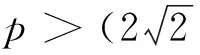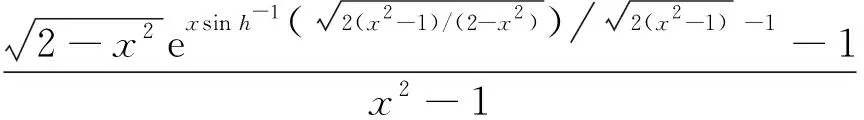Sándor-Yang平均关于经典平均凸组合的确界
2018-11-26张帆杨月英钱伟茂
张帆, 杨月英, 钱伟茂
(1. 湖州职业技术学院 建筑工程学院, 浙江 湖州 313000; 2. 湖州职业技术学院 机电与汽车工程学院, 浙江 湖州 313000;3. 湖州广播电视大学 远程教育学院, 浙江 湖州 313000)
0 引 言
2013年,YANG[1]介绍了4个Sándor-Yang平均:
(1)
其中,

(2)
(3)
分别为2个正数a和b的几何平均、算术平均、二次平均, Neuman-Sándor平均[2-3]和第二类Seiffert平均[4], 第一类Yang平均和第二类Yang平均[5-7].
设p∈R,a,b>0, 则调和平均H(a,b),反调和平均C(a,b)和p阶幂平均Mp(a,b)[8]分别定义为


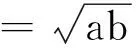
(4)
并且p阶幂平均Mp(a,b)对于固定的a,b>0和a≠b关于p∈R是连续和严格单调上升的.
不等式
H(a,b)=M-1(a,b) L(a,b) NS(a,b) C(a,b) 和 L(a,b) NS(a,b) 对所有a,b>0且a≠b均成立,其中,P(a,b)=(a-b)/[2sin-1((a-b)/(a+b))]和L(a,b)=(b-a)/(lnb-lna)分别为2个正数a和b的第一类Seiffert平均和对数平均. 最近, Sándor-Yang平均关于其他二元平均或其组合的比较研究取得了一定进展. 国内外学者证明了在特殊情形下一些涉及Sándor-Yang平均的重要不等式[1, 9-14]. Mα(a,b) Mλ(a,b) 对所有a,b>0且a≠b成立的最佳参数. 徐会作[13]证明了双向不等式 α1Q(a,b)+(1-α1)A(a,b) β1Q(a,b)+(1-β1)A(a,b), α2Q(a,b)+(1-α2)A(a,b) β2Q(a,b)+(1-β2)A(a,b), α3C(a,b)+(1-α3)A(a,b) β3C(a,b)+(1-β3)A(a,b), α4C(a,b)+(1-α4)A(a,b) β4C(a,b)+(1-β4)A(a,b) 对所有a,b>0且a≠b成立当且仅当α1≤1/3, 本文发现并证明了最佳参数α1,α2,α3,α4,β1,β2,β3,β4∈(0,1),双向不等式 α1A(a,b)+(1-α1)H(a,b) β1A(a,b)+(1-β1)H(a,b), α2A(a,b)+(1-α2)G(a,b) β2A(a,b)+(1-β2)G(a,b), α3Q(a,b)+(1-α3)A(a,b) β3Q(a,b)+(1-β3)A(a,b), α4C(a,b)+(1-α4)A(a,b) β4C(a,b)+(1-β4)A(a,b) 对所有a,b>0且a≠b均成立,并且推得一个新的不等式链: G(a,b) 为证明本文的主要结论, 需以下引理: 引理1设p∈(0,1), (1) 若p=5/6, 则对所有x∈(1,+∞)有f(x)<0; 证明经简单计算得 (5) (6) 其中, f1(x)=p(4-p)x6+2(3p2-2p-2)x4- (7p2-10p+3)x2+2(1-p)2. (7) 下面分2种情形讨论: (1) 当p=5/6时, 式(7)变为 (8) 对所有x∈(1,+∞)成立. 所以, 由式(5)、(6)和(8)易得对所有x∈(1,+∞)有f(x)<0. 6p-5=-1.878 4…<0, (9) 2p2+14p-11=-3.175 0…<0, (10) 3p2+8p-4=0.974 0…>0, (11) 式(7)和式(9)~(11)经简单计算可得 (12) (13) 其中,对所有x∈(0,+∞), f2(x)= 3p(4-p)x4+4(3p2-2p-2)x2- (7p2-10p+3), f2(1)=2p2+14p-11<0, (14) 4(3p2+8p-4)x>0. (15) 由式(14)和(15)可得,存在λ0∈(1,+∞),使得当x∈(1,λ0)时f2(x)<0,当x∈(λ0,+∞)时f2(x)>0. 由式(12)和(13)及当x∈(1,λ0)时f2(x)<0可知,f1(x)<0.由式(13)和当x∈(λ0,+∞)时f2(x)>0得到函数f1(x)在区间(λ0,+∞)上严格单调上升;则由式(12)和f1(λ0)<0及函数f1(x)在区间(λ0,+∞)上的单调性,可得存在λ1>λ0,使得当x∈(λ0,λ1)时f1(x)<0,当x∈(λ1,+∞)时f1(x)>0. 下面分2种情形讨论: 情形1x∈(1,λ1].易由式(5)和(6)及在区间(1,λ1)上f1(x)<0得到f(x)>0. 情形2x∈(λ1,+∞).由式(6)和f1(x)>0,得到函数f(x)在区间(λ1,+∞)上严格单调下降. 由式(5)和f(λ1)>0及函数f(x)在区间(λ1,+∞)上的单调性,可得存在λ>λ1>λ0∈(1,+∞),使得当x∈(λ1,λ)时f(x)>0,当x∈(λ,+∞)时f(x)<0. 引理2设p∈(0,1), (1) 若p=2/3, 则对所有x∈(1,+∞)有g(x)<0; 证明经简单计算可得 (16) (17) 其中, g1(x)=-(p2+4p-2)x3+2p2x+p(1-p). (18) 下面分2种情形讨论: (1) 当p=2/3时, 式(18)变为 (19) 且对所有x∈(1,+∞)成立. 所以, 由式(16)、(17)和(19)易得,对所有x∈(1,+∞)有g(x)<0. g1(1)=2-3p=0.439 2…>0, (20) -p2-12p+6=-0.513 7…<0 (21) 对所有x∈(1,+∞)…成立. 由式(20)和(21)可知,存在μ0∈(1,+∞),使得当x∈(1,μ0)时有g1(x)>0,当x∈(μ0,+∞)时有g1(x)<0. 下面分2种情形证明: 情形1x∈(1,μ0]. 根据式(16)和(17)及在区间(1,μ0)上g1(x)>0,可知g(x)>0. 情形2x∈(μ0,+∞).由式(17)和在区间(μ0,+∞)上g1(x)<0得到函数g(x)在区间[μ0,+∞)上严格单调下降.注意到式(16)变成 (22) 由不等式(22)和g(μ0)>0及函数g(x)在区间[μ0,+∞)上的单调性, 可得存在μ∈(μ0,+∞)⊂(1,+∞),使得当x∈(μ0,μ)时有g(x)>0,当x∈(μ,+∞)时有g(x)<0. 证毕. 引理3设p∈(0,1), 证明经简单计算可得 (23) (24) 其中, h1(x)= -p(1-p)x3-2(1-p)2x2+ p2-6p+3. (25) 下面分2种情形讨论: (1) 当p=1/3时, 式(25)变为 (26) h1(1)=1-3p=0.706 5…>0, (27) (28) 对所有x∈(0,+∞)成立. 下面分2种情形证明: 情形1x∈(1,σ0]. 由式(23)和(24)及在区间(1,σ0)上h1(x)>0,可知h(x)>0. 引理4设p∈(0,1), k(x)<0; 证明经简单计算可得 (29) (30) 其中, k1(x)=2p2x6+p(4-7p)x4+ 2(3p2-4p-1)x2-(p2+2p-3). (31) 下面分2种情形讨论: (1) 当p=1/6时, 式(31)变为 (32) 4-7p=3.716 3…>0, (33) p2+4p-1=-0.836 2…<0, (34) k1(1)=1-6p=0.756 8…>0, (35) 4(3p2-4p-1)x, (36) 由不等式(33)、(34)和等式(36)可知 (37) 下面分2种情形证明: 情形1x∈(1,τ0]. 由式(29)和(30)及在区间(1,τ0)上k1(x)>0,可知k(x)>0. 定理1双向不等式 α1A(a,b)+(1-α1)H(a,b) β1A(a,b)+(1-β1)H(a,b) H(a,b)=G(a,b)/x, (38) (39) 由式(38)和(39)有 (40) (41) (42) log[RGQ(a,b)]-log[pA(a,b)+(1-p)H(a,b)]= (43) 设 (44) 经简单计算可得 F(1+)=0, (45) (46) (47) 其中f(x)的定义见引理 1. 下面分2种情形证明: 情形1p=5/6. 由式(43)~(45)、(47)及引理1(1)得 (48) (49) 由式(43)~(45)、(49)及函数F(x)的分段单调性可知 (50) 所以, 定理1可由等式(48)和(50)结合下面的陈述得到. RGQ(a,b)>pA(a,b)+(1-p)H(a,b). RGQ(a,b) 定理2双向不等式 α2A(a,b)+(1-α2)G(a,b) β2A(a,b)+(1-β2)G(a,b) (51) (52) (53) ln[RGQ(a,b)]-ln[pA(a,b)+(1-p)G(a,b)]= ln(px+1-p)-1. (54) 设 ln(px+1-p)-1, (55) 经简单计算得 G(1+)=0, (56) (57) (58) 其中g(x)的定义见引理2. 下面,分2种情形证明: 情形1p=2/3. 由式(54)~(56)、(58)及引理2(1)得 (59) (60) 由式(54)~(56)、(60)及函数G(x)的分段单调性知 (61) 所以,由等式(51)~(53)和不等式(59)、(61)易得定理2. 定理3双向不等式 α3Q(a,b)+(1-α3)A(a,b) β3Q(a,b)+(1-β3)A(a,b) Q(a,b)=A(a,b)x, (62) RQG(a,b)= (63) 由式(62)和(63),得到 (64) (65) (66) ln[RQG(a,b)]-ln[pQ(a,b)+(1-p)A(a,b)]= ln(px+1-p)-1. (67) 设 ln(px+1-p)-1. (68) 经简单计算得 H(1+)=0, (69) (70) (71) 其中h(x)的定义见引理3. 下面,分2种情形证明: 情形1p=1/3.由式(67)~(69)、(71)及引理3(1)得 (72) (73) 由式(67)~(69)、(73)及函数H(x)的分段单调性知 (74) 所以, 定理3可由式(72)和(74)结合下面陈述得到. RQG(a,b)>pQ(a,b)+(1-p)A(a,b). RQG(a,b) 定理4双向不等式 α4C(a,b)+(1-α4)A(a,b) β4C(a,b)+(1-β4)A(a,b) 则由式(62),(63)和C(a,b)=A(a,b)x2可得 (75) (76) (77) ln[RQG(a,b)]-ln[pC(a,b)+(1-p)A(a,b)]= ln(px2+1-p)-1. (78) 设 ln(px2+1-p)-1. (79) 经简单计算得 K(1+)=0, (80) (81) (82) 其中k(x)的定义见引理4. 下面,分2种情形证明: 情形1p=1/6.由式(78)~(80)、(82)及引理4(1)得 (83) (84) 由式(78)~(80)、(84)及函数K(x)的分段单调性知 (85) 所以, 由等式(75)、(77)和不等式(83)、(85)易得定理4. 注记由定理2和定理3, 不难得到对所有a,b>0且a≠b,不等式链G(a,b)

1 引 理


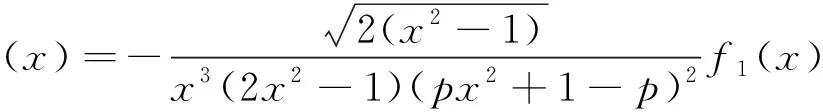


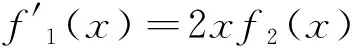


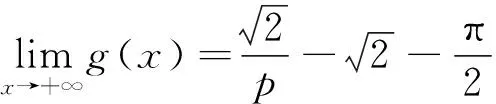

























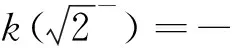





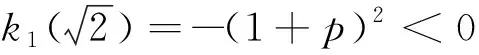




2 主要结果