， . .

(Grodno State University of Yanka Kupala, Grodno 230023, Republic of Belarus)

In the papers [1-2] the author considers the autonomous system of the following form

(1)

and investigates absence of movable multivalued singular points in its solutions. It is proved in the paper [3] that system [1-2] without movable multivalued singular points, derived possess one of two properties:

(2)

Δ=detA=0

(3)

where

In the paper [3] necessary conditions for the absence of multivalued singular points are obtained for the case when relations (2) and (3) do not hold. We will also considerakk≠0,k=1,2,3; In this case we can puta11=a22=a23=1.The coefficients of matrixAare placed in Table 1.

Table 1 The coefficients of matrix A

In the items 10, 11 and 12 numbersγis an integer.

The aim of this paper is to obtain analytical properties of solutions of systems which coefficients are placed in Table 1 as well to construct the first integrals of these systems.

Below we will use the following lemma.

Lemma1[4] 189 Ifurepresent Weierstrass Elliptic function, the general solution of the Lame equation

w″=(γ(γ+1)u+δ)w

is meromorphic, whereγ-natural numbers,δ′=0.

1 The main part

We present the analytic properties of the solutions of systems from Table 1, and also construct the first integrals of these systems.

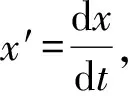
Theorem1

1) Systems (1) with coefficients contained in Table 1, These numbers: 1, 2, 4, 5, 6, 7, 8, 9,13,14, have meromorphic general solutions.

2) Systems (1) with coefficients contained in Table 1, These numbers: 10 (γ-natural number), 11,12 have rational general solutions.

3) Systems (1) with coefficients contained in Table 1, These numbers: 3～10 (γ-integer and negative) in solutions have logarithmic singular branch points.

Prove

1). In the first case we can write the system:

(4)

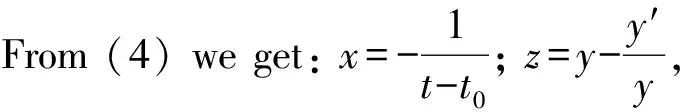
Then, applying the third equation of the system (4), we get:

y″=2y3+6x(y′-y2)

therefore

(5)

assuming

y=(t-t0)-2·ω(τ)-(t-t0)-1

τ=(t-t0)-1

(6)

we have:

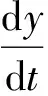
(t-t0)-2

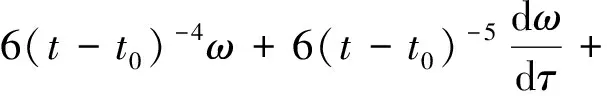
therefore, we get：

it implies:

(7)

whereHis an arbitrary interaction constant.

Remark： Below, the letter H or h denotes an arbitrary integration constant.

The solution of equation (7) can be expressed in terms of the Weierstrass Elliptic function, it’s mean,ω(τ) is a meromorphic function of the variableτ. Therefore, the general solution of system (4) is meromorphic.

2) Consider the system：

(8)

We denoteyz=2υ. Then:

(9)

For the functionυwe use (8) and (9) to construct the equation

it implie:

υ′2= 4υ3-H·υ

(10)

under the conditionH≠0, the functionυis the Weierstrass elliptic function.

Taking into account

The general solution of the system (9) is meromorphic.

3) From system

(11)

We find：

Assuming

we get

because

(12)

According to [5] 120-125,ω(τ) can be expressed in terms of the Weierstrass elliptic function.

It’s mean, system (11) has a solution:

4) For the system

(13)

u′2= 4u3+H

(14)

It’s mean, in the caseH≠0 functionuis Weierstrass elliptic function.

Assuming

we get

υ″=12uυ

(15)

Equation (15) is Lame equation and according to Lemma 1, the functionυis meromorphic.

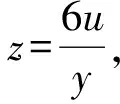
5) Suppose we have

(16)

Assumingxy=6u, we will successively get:

hence

u′2= 4u3+H

(17)

If

(18)

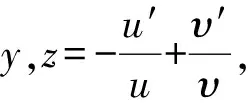
6) For system

(19)

We introducexy=2u.

it implies

u′2= 4u3+Hu

(20)

υ″=2uυ

According to Lemma 1, functionυis meromorphic, and with it have meromorphic functionsy,z,x.

7) Suppose we have

(21)

For functionu, we can construct the equation

(u′-u2)″=-(u′-u2)

Ifu′-u2=-6υ, Toυ″=6υ2,

it implies

υ′2= 4υ3+H

(22)

8) For the system

(23)

Ifu′-u2=-6υ, thenυ″=6υ2, it implies:

υ′2= 4υ3+H

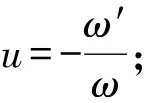
ω″=6υω

Hence, the functionω, and functionu,y,xand are meromorphics.

9) Have：

(24)

Assumingxy+y2=u, foruwe can get the equationu″=6u2, it implies u′2= 4u3+ H.

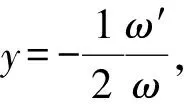
ω″=2uω

It’s mean, functionsx,y,ωandzare meromorphics.

10) We have：

(25)

Assumingy+z=υ, we getxz=υ2-υ′,υ″=3υυ′-υ3， it implies

wheret0,his an arbitrary constant, on the other hand, forx, we construct the equation

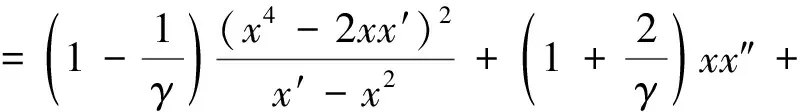
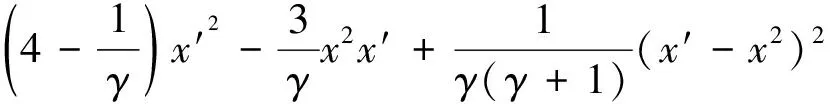
(26)

According to [6] whenγis an natural number, the equation (26) has a rational general solution. Obviously, functionszandywill become rational functions. Ifγis a negative integer, functionx,andz,ywill have movable logarithmic branch points.

11) For the system

(27)

We denotex+y=υ,xz=u.

Whenγis an natural numbers, we can find,x,y,zis rational functions. Ifγis a negative numbers， functionsy,ux,zwill have logarithmic branch points.

12) Suppose we have

(28)

We denoteγ+2=n,n≠0,1,2.

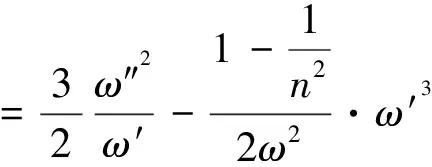
Simultaneously

(29)

Formulas (29) show that the general solution of system (28) is rational.

13) For the system

(30)

we introduce

and for the functionuwe construct the equation

it implies

u′2= 4u3+ 2Au+B

(31)

where

(γ-1)B=(2-γ)A=0

(32)

Ifγ=1 equation (32) is equation Lame,uis Weierstrass Elliptic function. Therefore,ωis meromorphic function, andx,yandzare meromorphic functions.

In the case ofγ=2, we will have

(33)

The characteristic equation for (33) has roots

So we can see that the general solution of the linear equation (33) does not contain logarithm, therefore, have form:

wherea0b0≠0,С1,C2— arbitrary constant.

14) We have

(34)

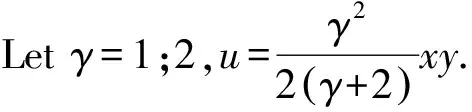
Then for the functionuwe construct equation

(35)

Whenν=1，2 equation (35) is Lame equation. It impliesωis meromorphic, thenx,yandzare meromorphic functions.

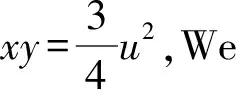
u′2=u4+ 8cu

(36)

wherecis an arbitrary integration constant

(37)

whereu=±(t-t0)-1-c(t-t0)2+…, thenu2=(t-t0)-2∓2c(t-t0)+…

The general solution of equation (37) will have the form

Theorem 1 is proved.

Theorem2

Whenν=1，2 and (34) whenν=4， systems (4)(8)(11)(13)(16)(19)(21)(23)(24)(25)(27)(28)(30)(34) have first integrals, as follows:

yz(yz-2(x-y)2)=Hx8

yz(yz-2(x+z)2)=H

xz(z-x-y)=Hy3

y2z2(3(x+z)2-2yz)=108H

x2y2(3(y+z)2-2xy)=108H

xy(2(y+z)2-xy)=H

xy[36y(y+z)3+xy(4xy-24y2-36yz-9z2)]=27H

3x2y2z2-24x2y4+36xy4z+36xy5+4x3y3-12x2y3z=27H

y2(2y2-6xy-xz)2-4y3(x+y)3=H

(y+z)2-2xz=hx2z2

(x+y)2-2xz=hx2z2

(xy)3-ν(x+y+z)2=4(xy)4-ν+H

Prove.

1) Taking into account

from (7) we get:

yz(yz-2(x-y)2)=Hx8

(38)

it is easy to verify that expression (38) is the first integral of the system(4).

2) By using (8) and (9), we can easily get the first integral of system (8):

yz(yz-2(x+z)2)=H

(39)

3) By

we get

(40)

With the help of (11)～(40) we find:

xz(z-x-y)=Hy3

(41)

It is easy to verify that expression (41) is the first integral of system (11).

4) By using (13), (14), we easily construct first integral of the system (13)：

y2z2(3(x+z)2-2yz)=108H

(42)

5) By using (17) the first integral of system (16) have form:

x2y2(3(y+z)2-2xy)=108H

(43)

6) By using (20),we construct the first integral of the system(19):

xy(2(y+z)2-xy)=H

(44)

7) By using (21) and (22) we can get the first integral of the system(21)

xy[36y(y+z)3+xy(4xy-24y2-

36yz-9z2)]=27H

(45)

8) The first integral of system (23) can be written as follows:

3x2y2z2-24x2y4+36xy4z+36xy5+

4x3y3-12x2y3z=27H

(46)

9) As in previous cases, we can find the first integral of system (24):

y2(2y2-6xy-xz)2-4y3(x+y)3=H

(47)

10) The first integral of system (25) has form

(y+z)2-2xz=hx2z2

(48)

11) It is easy to construct the first integral of system (27):

(x+y)2-2xz=hx2z2

(49)

12) Using (29) we obtain the first integral of the system (28):

(50)

13) By using (31) the first integral of system (30) can be written as follows：

(xy)3-γ(x+y+z)2=4(xy)4-γ+H

(51)

14) By using (31), we can write the first integral of system (34) as follow:

(52)

15) Ifγ=4, by using (36), we can easily construct the first integral of system (34):

xy(3(y+z)2-xy)2=H

H=27C2

(53)

Theorem 2 is proved.

2 Conclusion

We prove the theorems on the existence of meromorphic (in particular, rational) solutions for a class of the third-order autonomous systems, moreover the conditions for the existence of solutions with moving logarithmic branch points are derived. Additionally, the first integrals of considered systems are constructed. The results of the papers can be used in the analytical and qualitative theory of higher-order systems.

[1] KONOPLYANNIK I A.On a class of third-order systems without moving critical points[J].Differential equations,1975,11(8):1508-1511.

[2] KONOPLYANNIK I A.On a class of third-order systems with a single-valued solution[J].Differential equations,1975, 11(11):2094-2096.

[3] MARTYNOV I P.To the theory of third-order systems without moving critical points[J].Differential equations,1984,20(10):1720-1726.

[4] VINOGRADOV I M.Mathematical Encyclopedia[M].Moscow: Soviet Encyclopedia, 1982:1184.

[5] GOLUBEV V V.Lectures on the analytic theory of differential equations[M].Moscow: GITTL, 1950:463.

[6] MARTYNOV I P.Analytic properties of the solution of a third-order differential equation [J].Differential equations,1985, 21(5):764-771.