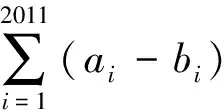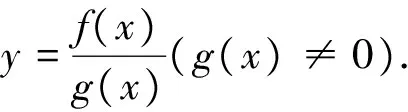广东省惠州市第一中学 (516007) 戴 飙

逆向思维是与正向思维相对的一种思维方式，当我们反复考虑某个问题陷入困境时，可考虑从问题的反面着手，执果索因，从不同于常规的角度思考，这种思维往往能使我们茅塞顿开，帮助我们找到解决问题的新思路.本文列举数例阐述逆向思维在数学解题中的妙用，以期达到抛砖引玉之效.

1.妙用分析法解题

分析法是从结论出发“执果索因”，步步寻求结论成立的充分条件，它只要求每相邻的两个论断中，后一个是前一个的充分条件即可(不一定等价).寻求从“未知”看“需知”，逐步靠拢“已知”.

证明：∵A+B+C=π,a、b、c>0.

评注：本题用直接法证明是很困难的，不妨改变思维方向进行逆向思维，采用分析法.由于三角形内角和为π，结合本题的结构特点，利用常量代换，即将π用A+B+C替换，从而开拓了新的解题途径，解法独特,闪烁出智慧的光芒！

这显然成立，故原命题成立.

评注：本题所给条件2tanA=3tanB,信息十分有限，根据条件想推出结论也显得比较困难，于是我们应转变传统的正向思维，采用逆向思维，从结论出发，寻找每步成立的充分条件.

2.巧用反证法解题

反证法是一种间接证法，即先提出一个与命题的结论相反的假设，然后从这个假设出发，经过正确的推理，导致矛盾，从而否定相反的假设，达到肯定原命题正确的一种方法.

(2)当α>β时,则有0

综上，α≥β不成立，∴α<β.故命题得证.

评注：本题从条件直接推导结论是很困难的，而采用分析法思维受阻，简直无法逆推.这时不妨从常规思路中跳出来，换一种逆向思维方式，从结论出发，在否定结论的前提下反向推出矛盾，问题则迎刃而解.

例4 (2011年全国高中数学联赛吉林省预赛试题)已知a1,a2,…,a2011是一列互不相等的正整数，如果任意改变这2011个数的顺序，把它们记为b1,b2,…,b2011，则数M=(a1-b1)(a2-b2)(a3-b3)…(a2011-b2011)的值( ).

A.必为0B.必为1C.是奇数D.是偶数

所以假设不成立，即M是偶数，显然M存在不为零的值,则选项A不正确，故选D.

评注：本题借用“正难则反”的思想进行求解，体现了一种逆向思维的数学途径，有助于提高学生发散思维能力，拓宽数学视野，同时能激发学生学习数学的兴趣.

3.借用逆否命题解题

当我们直接证明原命题有困难时,变换角度,可以考虑证明它的逆否命题.从某种程度而言这也是一种转换的思想，这种转换往往能寻求到顺利解决问题的切入点，达到事半功倍的效果.

例5 已知函数y=f(x)在(-∞,+∞)上是增函数，m,n∈R,证明：若f(m)+f(n)≤f(-m)+f(-n),则m+n≤0.

证明：本题直接证明较困难，于是可考虑证明此命题的逆否命题，“若f(m)+f(n)≤f(-m)+f(-n),则m+n≤0”视为原命题，其逆否命题是：“若m+n>0，则f(m)+f(n)>f(-m)+f(-n).”

∵m+n>0,∴m>-n,n>-m,又函数y=f(x)在(-∞,+∞)上是增函数，∴f(m)>f(-n),f(n)>f(-m),⟹f(m)+f(n)>f(-m)+f(-n)，∴命题“若m+n>0，则f(m)+f(n)>f(-m)+f(-n).”为真，∴原命题“若f(m)+f(n)≤f(-m)+f(-n),则m+n≤0”也为真.故原命题得证.

评注：本题采用逆向思维，破除顺推定势，巧妙转化为其逆否命题.此解法向我们显明，逆向思维的灵活性为数学学习注入了生机与活力，也增加了数学学习的趣味性.

4.逆用运算法则及定理解题

数学中一些运算法则及定理具有双向性,可逆性.但学生由于受思维定势的影响,往往只注意正向思考.教学中如果我们重视运算法则、定理,公式等逆向使用，学生不但对所学知识理解得更透彻，而且还能养成双向考虑问题的习惯，在运用中能左右逢源,融会贯通.

例6 在△ABC中，求证：sin2A+sin2B-sin2C=2sinAsinBcosC.

评注：本题将左边的式子巧妙变形，逆用正、余弦定理，解法新颖，充分展示了逆向思维是一种创造性思维方式，有利于帮助学生树立创新意识，从而激发学生的求知欲和好奇心，提高学习数学的兴趣，也充分展示出数学的无限魅力！

例7 已知函数f(x)的导数为f′(x)，f(x)不是常数函数，且(x+1)f(x)+xf′(x)≥0，对x∈[0,+∞)恒成立，则下列不等式一定成立的是( ).

A.f(1)<2ef(2)B.ef(1)

C.f(1)<0D.ef(e)<2f(2)

解：由(x+1)f(x)+xf′(x)≥0得：xf(x)+[f(x)+xf′(x)]=xf(x)+[xf(x)]′≥0,设F(x)=ex[xf(x)],那么F′(x)=ex[xf(x)]+ex[xf(x)]′=ex{xf(x)+[xf(x)]′}≥0，∴函数F(x)=ex[xf(x)]在x∈[0,+∞)上是单调递增函数，则F(1)

评注：当题设条件中存在或通过变形出现特征式“f′(x)g(x)+f(x)g′(x)”时，可联想、逆用积的求导法则，构造可导函数y=f(x)g(x).特别地，若f′(x)+f(x)≥0,构造F(x)=exf(x)，则F′(x)=ex[f′(x)+f(x)]≥0.

数学逆向思维有利于丰富学生的思维方式，打开学生的数学解题思路，使得学生能够学会从不同的角度、以不同的方法尝试解决问题.这不仅唤起学生的求知欲和好奇心，还能激发起学生的创造性思维，有利于帮助学生树立创新意识.值得注意的是：正向思维有它很大的积极性的一面，但决不能一味地追求逆向思维的训练，否则适得其反.要结合所教学生的实际情况，因材施教，适当、适度地渗透逆向思维在数学解题中的妙用，以达到启迪数学智慧的目的.