，*，

(1.安徽理工大学 机械工程学院，安徽 淮南 232001；2.南通鹏飞铸造有限公司，江苏 南通 226623)

为了提高铸造过程中组芯工艺的效率和精确性，在传统工艺流程中引进组芯机器人替代人工在复杂工作环境下完成铸造过程中的组芯工序已成为市场形势所趋[1].目前，机器人在组芯工序中的应用仅局限于对砂芯的浸涂，研究中的六自由度机器人则能实现将砂芯准确装入砂箱，该工序不仅要求机器人工作中末端执行器达到目标位置，也对执行器的姿态精度提出较高要求.机器人逆运动学的求解问题是研究机器人运动控制和轨迹规划的基础，通过已知工具坐标系相对工作台坐标系的期望位置和姿态，求解机器人到达预期位姿的关节变量.该问题的求解过程存在方程参数多、解的非线性和强耦合性等问题，一直是国内外研究的难点.通常情况下，机器人的运动学建模都会采用D-H矩阵参数法，但是该方法存在局部坐标系过多、几何意义不明显等缺点.因此，寻求一种高效、简单的数学工具来进行机器人运动学建模成为当前机器人领域热点之一.

旋量法[2]是用一组对偶矢量的螺旋来表示物体运动的角速度和线速度.相比于传统D-H矩阵的参数法，旋量法的优势在于从整体上描述刚体的运动，避免局部坐标系描述时所造成的奇异性；对刚体运动进行几何描述，可以简化机构的分析；具有明显的几何意义优点，使用指数积进行逆解求解时，可以明确多解的条件与个数.

为求解机器人运动学逆解问题，首先要解决一般机器人设计中遇到的逆解子问题，然后设法将整个运动学逆问题分解成若干个解为已知的子问题.其中最著名的是Paden-Kahan子问题，建立于Kahan[3]的著作中.吕世增[4]等采用吴方法对一般机器人运动学方程进行消元，实现了计算机机械化求解.李盛前[5]等在旋量理论的基础上引入sylvester结式进行逆运动学求解，并在数学符号化运算软件Maple中实现了逆解算法过程.李悦[6]等利用旋量理论对RRRP机器人进行运动学建模并且获得机器人逆解算法.钱东海[7]等利用Paden-Kahan子问题简化旋量理论求解六轴机器人逆解问题过程，得到精确的机器人逆解.Akad Nankl[8]利用旋量理论模拟了机器人在空间中的运动情况.Dinesh[9]等利用常规消元法对6R机械臂进行逆运动学求解.李君[10]等利用旋量理论对StanFord臂进行运动学建模，并得到了Satnford臂的雅各比矩阵.

研究基于旋量理论基础对六自由度组芯机器人进行逆运动学分析，结合Paden-Kahan子问题算法对组芯机器人的各关节转动的角度进行求解.

1 旋量理论

在欧氏空间中，质点的瞬心位置可相对于惯性坐标系来描述.根据chasles定理[11]，任何刚体的运动都可以转化为绕某一轴的转动加上平行于该轴的移动来实现，即为旋量运动.

假设刚体坐标系B的原点相对于坐标系A的位置矢量为PAB∈R3,姿态矢量RAB∈SO(3)(SO(3) 是三维旋转群)，则系统由(RAB,PAB)确定，用齐次坐标可以表示为：

(1)

根据旋量理论，刚体的变换可以表示为运动旋量的指数，其表达式为：

(2)

在刚体上的物体坐标系T相对于惯性坐标系S的位姿变换用gst(θ)表示，以gst(0) 表示刚体相对于惯性坐标系的起始位姿，那么，相对于惯性坐标系的最终位姿为：

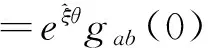
(3)

因此，对于一个运动旋量来说，指数变换反映的是刚体的相对运动，运动旋量的指数可以理解为描述刚体由起始到最终位形的变换.

2 Paden-Kahan子问题

2.1 子问题1

设ξ为一个零节距的单位运动螺旋，p、q∈R3是空间两点，点P绕轴旋转θ角到达q点，如图1所示.假定r是轴ξ上的一点，定义r与q之间的矢量为u=(p-r)，r与q之间的矢量为v=(q-r)，u′和v′分别为u，v在垂直于轴ξ平面上的投影.文献[11]给出了该问题的求解公式：

θ=atan(ωT(u′×v′),u′Tv′),

(4)

2.2 子问题2

设ξ1和ξ2为两个零节距、轴线相交的单位运动螺旋，p、q∈R3是两点，点p先绕轴ξ1旋转θ1角到达c点，然后绕轴ξ2旋转θ2角到达q点，如图2所示.若两个轴线平行，则该问题退化为子问题1，且满足θ1+θ2=θ的任意θ1，θ2都是正确解.如果两个轴线不平行，设c满足下式：

(5)

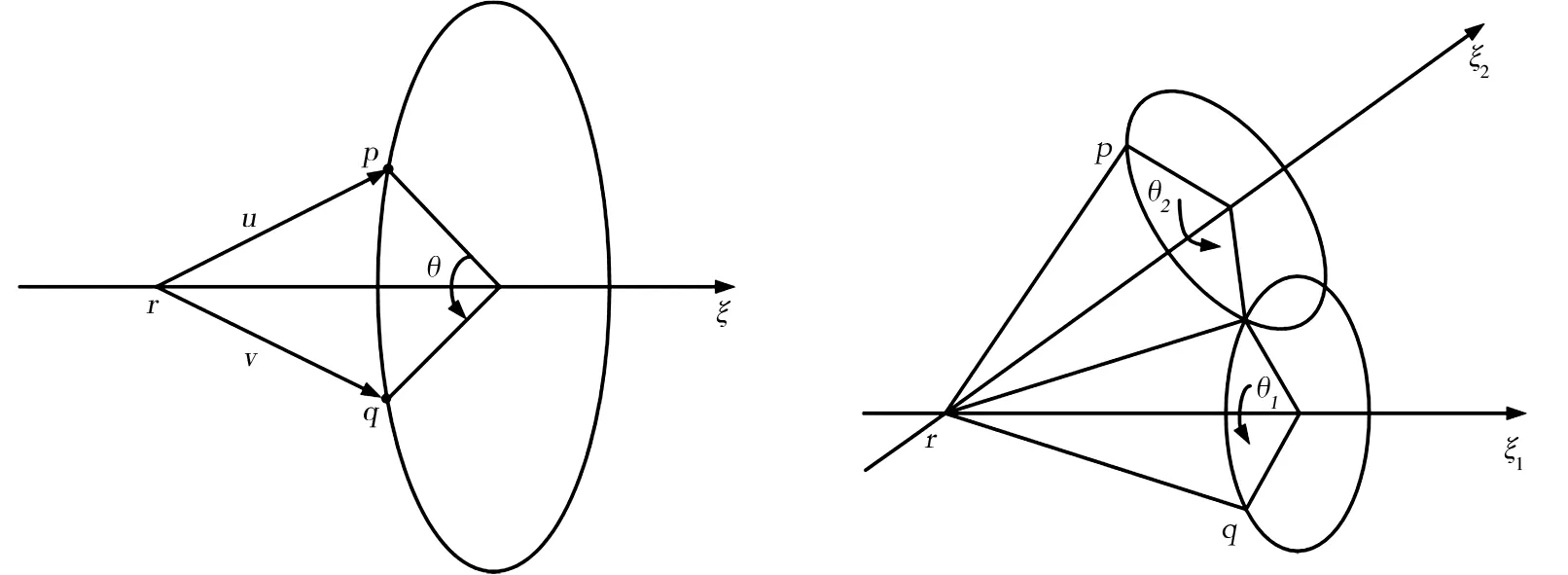
图1 绕单轴的螺旋运动图2 绕两轴的螺旋运动

定义向量u=(p-r),v=(q-r),z=(c-r),则得到：

(6)

因为‖u‖2=‖z‖2=‖v‖2，且ω1,ω2,ω3是线性独立的，所以得到下式：

z=αω1+βω2+γ(ω1×ω2),

(7)

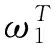
(8)

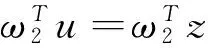
(9)

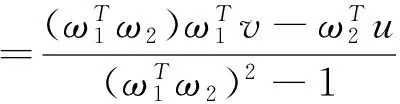
(10)

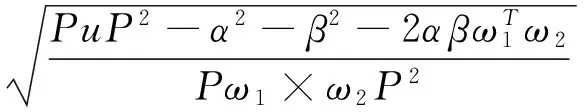
(11)

式(11)存在0,1或2个实根的情况.在有根的情况下，将α,β,γ值代入即可求得z和c，然后利用子问题1可以求得θ1和θ2的值.

3 组芯机器人逆运动学求解算法

3.1 组芯机器人运动学建模

六自由度组芯机器人机械结构如图3所示，各连杆坐标系结构简图如图4所示.此类机器人各关节通过转动副连接.前3个关节确定手腕参考点位置，后3个关节确定手腕的姿态.与D-H矩阵参数法不同，旋量法选取的坐标系是世界坐标系.设各连杆旋转轴ξi的单位矢量为ωi(I=1,2,…,6) ，关节轴转动的角度为θi，连杆i的坐标原点为θi.将各关节的运动加以组合，即得运动学正解映射为：

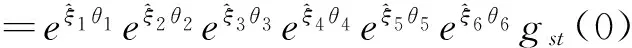
(12)

式(12)为机器人运动学正解的指数积公式.

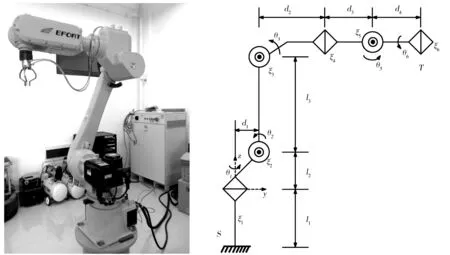
图3 六自由度组芯机器人图4 组芯机器人结构简图

3.2 组芯机器人逆运动学求解

根据Pieper准则：相邻关节的轴线相交于一点，或3个轴线相互平行，则对于任意给定的末端工具的位置和姿态都有运动学逆解.组芯机器人属于六自由度关节转动机器人，其4,5,6三轴的轴线均交于同一点，满足Pieper准则，所以该机器人存在封闭解.

给定机器人的末端工具坐标系T，机器人的基座惯性坐标系S，则机器人各个轴转动角度为0时，基础坐标系与工具坐标系的转换为：

(13)

(1)θ1的求解.根据chalse定理：如果一点位于旋转轴上，无论该点绕旋转轴旋转多少角度，该点的坐标不变，即：

(14)

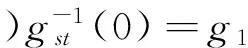
(15)

将式(15)右乘qw，根据上述定理可得：

(abc)T,

(16)

将式(16)展开得：

L(c2s1s3+c3s1s2)-D(c2c3s1-s1s2s3)+m=a,

(17)

D(c1c2c3-c1s2s3)-L(c1c2s3+c1c3s2)+n=b,

(18)

D(c2s3+c3s2)+L(c2c3-s2s3)+k=c,

(19)

m=-s1[s2(l1+l2)-d1(c2-1)]-c2s1[Ls3-d1(c3-1)]-s1s2[d1s3+L(c3-1)]

n=c1[s2(l1+l2)-d1(c2-1)]+c1c2[Ls3-d1(c3-1)]+c1s2[d1s3+L(c3-1)]

k=-(l1+l2)(c2-1)-c2[d1s3+L(c3-1)]-d1s2+s2[Ls3-d1(c3-1)]

式中，ci(i=1∶6)是cosθi的缩写，si是sin(θi)的缩写.

式(17)乘以c1加上式(18)乘以s1得到下式：

acosθ1+bsinθ1=0,

解上述方程，可得：

(20)

(2)θ2和θ3的求解.组芯机器人的2轴和3轴是两个平行的关节，qn绕轴2旋转θ2后到达点c，再绕轴3旋转θ3角度后到达qw点，取qn=[qnxqnyqnz]T根据子问题2的方法，可得：

φ1=arctan(-l2(qny-d1),-l2(l1-qnz)),

(21)

c,r23的夹角Δ1为：

(22)

则可求得θ2

θ2=φ1±Δ1,

(23)

同理

φ2=arctan(-l2(d2+d3),-l2l3),

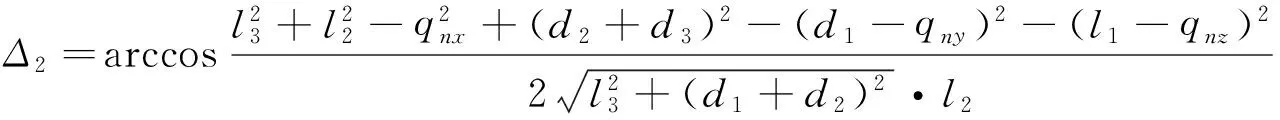
则可求得θ3

θ3=φ2±Δ2,

(24)

(3)θ4和θ5的求解.根据得到的θ1,θ2和θ3值，由式(12)可得：

(25)

取在轴6上而不在轴4,5上的点qm=[0D+d4L]T

将qm点带入式(25)中，得：

qmyqmz]T,

(26)

根据式(9),式(10)，式(11)可得：

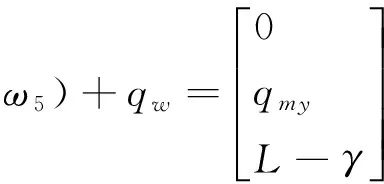
(27)

根据式(4)得：

×c),cTv)=arctan((γ-L)qmx,qmy(qmy-D)-(L-qmz)(L-γ)),

(28)

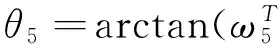
(29)

(4)θ6的求解.将前面得到5个轴的转动角度代入式(12)可得：

(30)

取不在轴6上的任意点(该点选取时尽量选择较远处点，u可近似等于u在ω垂直的平面投影) ，po=[ijk]T,将po点带入式(30)中，得：

根据子问题1的方法可求θ6

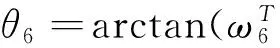
arctan(i(L-poz)-pox(L-K),(D-j)(D-poy)+(L-K)(l-poz)+poxi).

(31)

4 逆解算法的实例验证

组芯机器人的具体参数如下：l1=404 mm，l2=100 mm，l3=780 mm，d1=170 mm，d2+d3=760 mm，d4=125 mm，具体求解六自由度组芯机器人逆解过程如下：

(1)随机给定每个关节的对应转动角度.

θ1=-32.45°,θ2=-32.20°,θ3=-1.15°,θ4=0°,θ5=-58.66°,θ6=-32.42°.

(2)根据机器人正运动学指数积公式计算末端执行器的位姿.

(3)应用研究所给出的求解逆解的方法，在Matlab软件中编制逆运动学算法程序，将数据代入后共得到8组逆解，如表1所示.

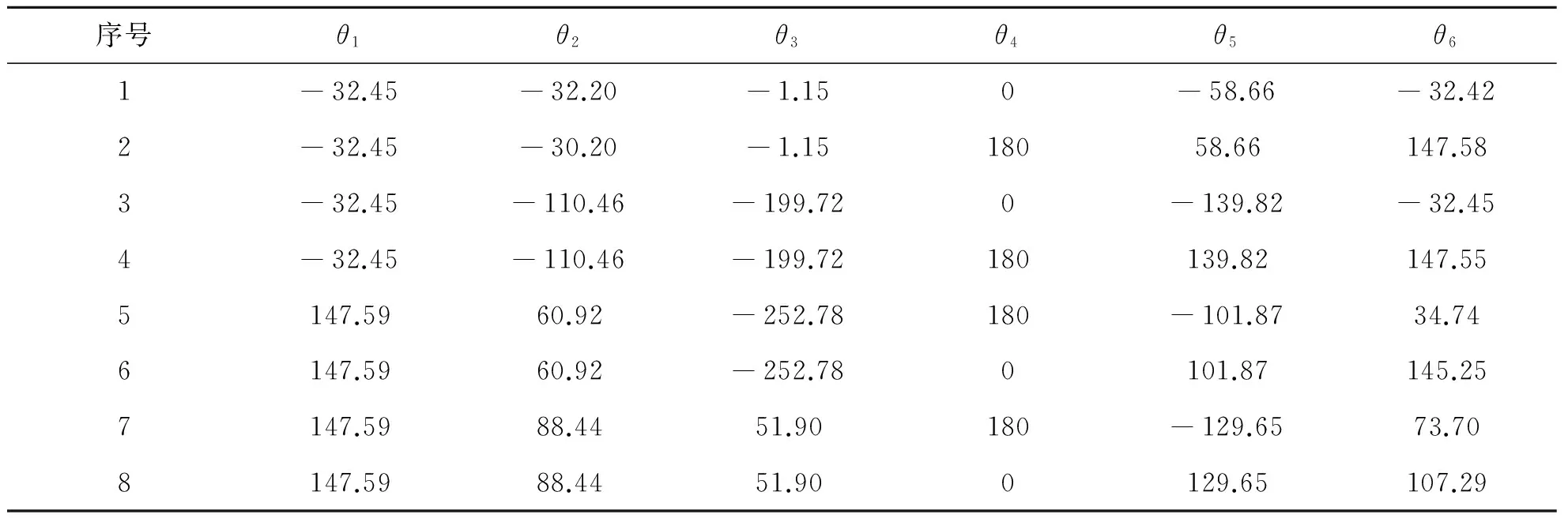
表1 8组运动学逆解

将上述8组逆解代入机器人正运动学公式，得到的位姿解与设定解相对误差在0.2%以内，所以该逆解算法具有较高的精确度.

5 结论

基于旋量理论对六自由度组芯机器人进行运动学建模，针对组芯机器人结构特殊性，利用Paden-Kahan子问题算法对逆解求解过程进行简化，从而求得了机器人的位姿，并对结果进行了验证.该逆运动学求解算法从整体上描述了机器人的运动，避免了传统D-H参数方法求解过程中复杂的坐标转换，简化了运算过程，减少了控制系统运算的时间；同时描述了组芯机器人组芯作业时末端手爪的姿态和各轴的运动参数，为组芯机器人精确组芯的控制提供了理论依据.

[1] 林祖盛.ABB机器人在铸造组芯整体浸涂上的应用[J].科技经济导刊，2016(33)：74-75.

[2] R S BALL.A treatise on the theory of screws[M].UK：Cambrige University Press,1900.

[3] K HUNT.H kinematic geometry of mechanisms[M].UK:Oxford University press,1978.

[4] 吕世增，张大卫,刘海年.基于吴方法的6R机器人逆运动学旋量方程求解[J].机械工程学报，2010，46(17)：35-41.

[5] 李盛前，谢小鹏.基于旋量理论和Sylvester结式法的6自由度机器人逆运动学求解分析[J].农业工程学报，2015,31(20):48-54.

[6] 李悦，周利坤.基于旋量理论的RRRP机器人逆运动学分析与研究[J].机械科学与技术，2014，33(6):820-824.

[7] 钱东海，王新峰,赵伟，等.基于旋量理论和Paden-Kahan子问题的6自由度机器人逆解算法[J].机械工程学报，2009,45(9):72-77.

[8] F M DIMENTBERG.Determination of the motion of spatial mechansims (Russian)[M].Moscow:Akad Nank,1950.

[9] DINESH MANOCHA,F C JOHN.Efficient inverse kinematic for general 6R manipulator[J].IEEE Transactions on Robotics and Automation,1994,10(5):648-657.

[10] 李君.基于旋量理论的Stanford臂的运动学分析[J].天津科技大学学报，2010,25(4):72-75.

[11] 理查德.机器人操作的数学导论[M].北京:机械工业出版社，1994.