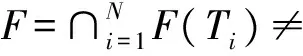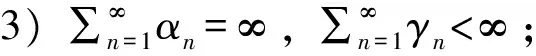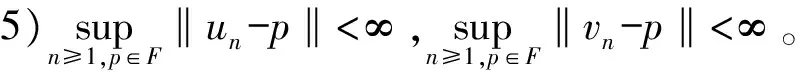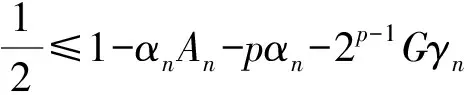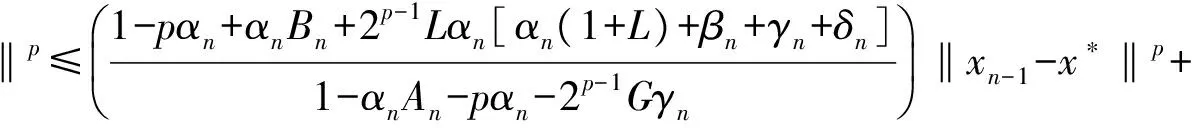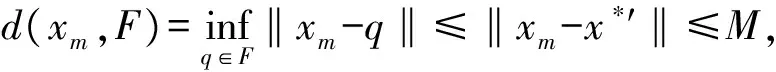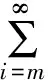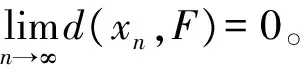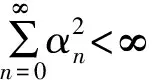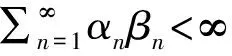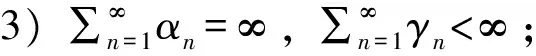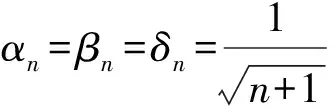有限族严格伪压缩映象公共不动点的强收敛定理
2018-02-02张树义丛培根
张树义,丛培根,林 媛
(渤海大学数理学院,辽宁 锦州 121013)
1 引言与预备知识
设E是实Banach空间,E*是E的对偶空间。对偶映象Jp:E→2E*(1 定义1 设K是实Banach空间E的闭子集,T:K→K称为是半紧的, 如果对K中的任意有界序列{xn},‖xn-Txn‖→0(n→∞),存在子列, 使得xni→x*∈K(i→∞)。 定义2 设K是实Banach空间E的闭子集,T:K→K 1)T称为是非扩张的, 如果∀x,y∈K, 有‖Tx-Ty‖≤‖x-y‖。 2)T称为是依Brower和Petryshyn意义k-严格伪压缩的, 如果存在k∈(0,1)使得对∀x,y∈K,存在jp(x-y)∈Jp(x-y)使得 〈Tx-Ty,jp(x-y)〉≤‖x-y‖p-k‖x-y-(Tx-Ty)‖p。 (1) 如果I表示恒等映象, 则式(1)可以写成下列形式 〈(I-T)x-(I-T)y,jp(x-y)〉≥k‖(I-T)x-(I-T)y‖p。 (2) 注1: Browder-Petryshyn型严格伪压缩映象一定是Lipschitzian连续的。事实上, 由(2),有 (3) 其中:n≥1;Tn=Tn(modN);{αn}、{βn}、{γn}、{δn}是[0,1]中4个实数列,满足αn+γn≤1和βn+δn≤1;∀n≥1 {un}和{vn}是K中2个有界序列。 使用迭代过程式(3), Gu[6]在Banach空间中证明下列定理。 定理G2[6]设E是实Banach空间,K是E的非空闭凸子集。T:K→K是半紧的严格伪压缩映象,F(T)={x∈K:Tx=x}≠∅。设{αn}、{βn}、{γn}、{δn}是[0,1]中4个实数列,满足αn+γn≤1和βn+δn≤1,n≥1,{un}和{vn}是K中2个有界序列满足下列条件: 另一方面,文献[8-17]使用新的分析方法, 研究了一些非线性映象不动点的迭代逼近问题。 受上述工作的启发, 本文的目的是在赋范线性空间, 使用条件(A′), 研究一族严格伪压缩映象合成隐式迭代过程式(3)定义的序列{xn}的收敛性。 本文的研究结果, 改进了文献[6]中的相关结果。 下面回忆一些预备知识。 对有限族映象Ti:K→K(i=1,2,…,N), 修正这一条件如下: 注3:如果N=1, 则条件(A′)便是条件(A)。 下列引理在本文中将被用到。 引理1[8]设E是任意实赋范线性空间,JP:E→2E*是对偶映象, 则x,y∈E,1 ‖x+y‖p≤‖x‖p+2〈y,jp(x+y)〉,∀jp(x+y)∈Jp(x+y)。 1)αn+γn≤1和βn+δn≤1,∀n≥1; 2)αn→0,βn→0,δn→0(n→∞); 4)αnβnL2<1,其中L=max1≤i≤N{Li}; 证明因每一Ti:K→K,i∈I={1,2,…,N}是严格的伪压缩映象, 所以存在常数ki∈(0,1)和Li≥1, 使得∀x,y∈K,i∈I, 〈Tix-Tiy,jp(x-y)〉≤‖x-y‖p-ki‖x-Tix-(y-Tiy)‖p和‖Tix-Tiy‖≤Li‖x-y‖。设k=min1≤i≤N{ki},L=max1≤i≤N{Li},则 〈Tix-Tiy,jp(x-y)〉≤‖x-y‖p-k‖x-Tix-(y-Tiy)‖p,∀i∈I, (4) 和‖Tix-Tiy‖≤L‖x-y‖,∀i∈I。设x*∈F,由式(3)、式(4)和引理1有 ‖xn-x*‖p=‖(1-αn-γn)(xn-1-x*)+αn(Tnyn-x*)+γn(un-x*)‖p≤ (1-αn-γn)p‖xn-1-x*‖p+pαn〈Tnyn-x*,jp(xn-x*)〉+pγn〈un-x*,jp(xn-x*)〉≤ (1-αn-γn)p‖xn-1-x*‖p+pαn〈Tnyn-Tnxn,jp(xn-x*)〉+ pαn〈Tnxn-x*,jp(xn-x*)〉+pγn〈un-x*,jp(xn-x*)〉≤ (1-αn)p‖xn-1-x*‖p+pαn‖Tnyn-Tnxn‖·‖xn-x*‖p-1+pαn‖xn-x*‖p- pαnk‖xn-Tnxn‖p+pγn‖un-x*‖·‖xn-x*‖p-1≤ (1-αn)p‖xn-1-x*‖p+pαnL‖yn-xn‖·‖xn-x*‖p-1+pαn‖xn-x*‖p- pαnk‖xn-Tnxn‖p+pγn‖un-x*‖·‖xn-x*‖p-1。 (5) 由式(3), 有 ‖yn-xn‖=‖βn(Tnxn-xn-1)+δn(vn-xn-1)+αn(xn-1-Tnyn)+γn(xn-1-un)‖≤ βn‖Tnxn-xn-1‖+δn‖vn-xn-1‖+αn‖xn-1-Tnyn‖+γn‖xn-1-un‖≤ βn‖Tnxn-x*‖+βn‖xn-1-x*‖+δn‖vn-x*‖+δn‖xn-1-x*‖+ αn‖xn-1-x*‖+αn‖Tnyn-x*‖+γn‖xn-1-x*‖+γn‖un-x*‖≤ βnL‖xn-x*‖+αn‖xn-1-x*‖+βn‖xn-1-x*‖+γn‖xn-1-x*‖+ δn‖xn-1-x*‖+αnL‖yn-x*‖+γn‖un-x*‖+δn‖vn-x*‖≤ βnL‖xn-x*‖+(αn+βn+γn+δn)‖xn-1-x*‖+ αnL‖yn-x*‖+γn‖un-x*‖+δn‖vn-x*‖。 (6) 和 ‖yn-x*‖=‖(1-βn-δn)(xn-1-x*)+βn(Tnxn-x*)+δn(vn-x*)‖≤ (1-βn-δn)‖xn-1-x*‖+βn‖Tnxn-x*‖+δn‖vn-x*‖≤ ‖xn-1-x*‖+βnL‖xn-x*‖+δn‖vn-x*‖。 (7) 令G=max{sup{‖un-x*‖:n≥1,x*∈F},sup{‖vn-x*‖:n≥1,x*∈F}}。 将式(7)代入式(6), 再将式(6)代入式(5), 并应用pap-1b≤2p-1(ap+bp),其中a,b∈[0,+∞), 有 ‖xn-x*‖p≤(1-αn)p‖xn-1-x*‖p+pαnL(βnL+αnβnL2)‖xn-x*‖p+ pαnL(α+βn+γ+δn+αnL)‖xn-1-x*‖·‖xn-x*‖p-1+ pαnγnL‖un-x*‖·‖xn-x*‖p-1+pαnL(δn+αnδnL)‖vn-x*‖·‖xn-x*‖p-1+ pαn‖xn-x*‖p-pαnk‖xn-Tnxn‖p+pγn‖un-x*‖·‖xn-x*‖p-1≤ (1-αn)p‖xn-1-x*‖p+pαnβnL2(1+αnL)‖xn-x*‖p+ 2p-1αnL[αn(1+L)+βn+γn+δn](‖xn-1-x*‖p+‖xn-x*‖p)+ 2p-1αnγnGL(1+‖xn-x*‖p)+2p-1αnδnL(1+αnL)G(1+‖xn-x*‖p)+ pαn‖xn-x*‖p-pαnk‖xn-Txn‖p+2p-1γnG(1+‖xn-x*‖p)= {(1-αn)p+2p-1αnL[αn(1+L)+βn+γn+δn]}‖xn-1-x*‖p+ [pαnβnL2(1+αnL)+2P-1αnL(αn(1+L)+βn+γn+δn)‖+ 2p-1αnγnLG+2p-1αnδnL(1+αnL)G+pαn+2p-1Gγn]‖xn-x*‖p+ 2p-1γn(1+αnL)G+2p-1αnδnL(1+αnL)G-pαnk‖xn-Tnxn‖p≤ [(1-αn)p+2p-1αnL(αn(1+L)+βn+γn+δn)]‖xn-1-x*‖p+ (αnAn+pαn+2p-1Gγn)‖xn-x*‖p+2p-1γn(1+L)G+ 2p-1αnδnL(1+L)G-pαnk‖xn-Tnxn‖p, (8) 其中An=pβnL2(1+L)+2p-1L[αn(1+L)+βn+γn+δn]+2p-1γnLG+2p-1δnL(1+L)G。注意到 其中 因1-αnAn-pαn-2p-1Gγn→1(n→∞),所以存在正整数n1,∀n≥n1,有 [1+2(αnAn+2p-1Gγn+αnBn+2p-1Lαn(αn(1+L)+βn+γn+δn))]‖xn-1-x*‖p+ 2p(γn+αnδnL)(1+L)G-pαnk‖xn-Tnxn‖p。 (9) 注意到Tn=Tn(modN),n(modN)∈{1,2,…,N},由式(9)有 ‖xn-x*‖p≤(1+2(αnAn+2p-1Gγn+αnBn+2p-1Lαn[αn(1+L)+βn+γn+δn]))‖xn-1-x*‖p+ 2p(γn+αnδnL)(1+L)G-pαnk‖xn-T1xn‖p, ‖xn-x*‖p≤(1+2(αnAn+2p-1Gγn+αnBn+2p-1Lαn[αn(1+L)+βn+γn+δn]))‖xn-1-x*‖p+ 2p(γn+αnδnL)(1+L)G-pαnk‖xn-T2xn‖p, ⋮ ‖xn-x*‖p≤(1+2(αnAn+2p-1Gγn+αnBn+2p-1Lαn[αn(1+L)+βn+γn+δn]))‖xn-1-x*‖p+ 2p(γn+αnδnL)(1+L)G-pαnk‖xn-TNxn‖p。 将上面不等式相加并使用条件(A′), 得 ‖xn-x*‖p≤(1+2(αnAn+2p-1Gγn+αnBn+2p-1Lαn[αn(1+L)+βn+γn+δn]))‖xn-1-x*‖p+ (1+2(αnAn+2p-1Gγn+αnBn+2p-1Lαn[αn(1+L)+βn+γn+δn]))‖xn-1-x*‖p+ 2p(γn+αnδnL)(1+L)G-pαnk{f(d(xn,F))}P。 对x*∈F取下确界, 有 [d(xn,F)]p≤(1+2(αnAn+2p-1Gγn+αnBn+2p-1Lαn[αn(1+L)+βn+γn+δn]))[d(xn-1,F)]p+ 2p(γn+αnδnL)(1+L)G-pαnk{f(d(xn,F))}p≤ [d(xn-1,F)]p+2αn[An+Bn+2p-1L(αn(1+L)+βn+δn)][d(xn-1,F)]p+ (2+2pL)γn[d(xn-1,F)]p+2pγn(1+L)G+ 2pαnδnL(1+L)G-pαnk{f(d(xn,F))}p。 (10) 下面用归纳法证明∀n≥m,有 (11) 这蕴含d(xn+1,F)>M。由f的单调递增性, 有f(d(xn+1,F))≥f(M)。由式(10)可得 [d(xn+1,F)]p≤[d(xn,F)]p+((2+2pL)(2M)p+2p(1+L)G)γn+1- [d(xn,F)]p+((2+2pL)(2M)p+2p(1+L)G)γn+1≤ 这是一个矛盾。因此当∀n≥m时, 式(11)成立。由式(11)有 进而∀n≥m, 有d(xn,F)≤2M。于是, 由式(10), ∀n≥m, 有 [d(xn,F)]p≤ [d(xn,F)]p+2αn[An+Bn+2p-1L(αn(1+L)+βn+δn)](2M)p+ (2+2pL)γn(2M)p+2pγn(1+L)G+2pαnδnL(1+L)G-pαnk{f(d(xn,F))}p。 (12) 注4:定理1从以下方面改进与推广了定理G2: 1) 推广定理G2从Banach空间到赋范线性空间; 2)半紧的条件被条件(A′)取代; 5) 我们的证明与已往有很大的不同。 注5:定理1也改进与推广了文献[1-5,7]中的相应结果。 取N=1, 则式(3)变为: (13) 于是有 定理2 设E是实赋范空间,K是E的一非空闭凸子集。T:K→K是严格的伪压缩映象,F(T)={x∈K:Tx=x}≠∅。假设{αn}、{βn}、{γn}、{δn}是[0,1]中4个实数列,{un}和{vn}是K中2个有界序列, 满足下列条件: 1)αn+γn≤1和βn+δn≤1,∀n≥1; 2)αn→0,βn→0,δn→0(n→∞); 4)αnβnL2<1; 对x0∈K,{xn}是式(13)定义的合成隐式迭代序列。如果满足条件(A), 且∀x*∈F,{‖xn-x*‖}单调递减,则序列{xn}强收敛T的一公共不动点。 [1]BROWDER F E, Petryshyn W V.Construction of fixed points of nonlinear mappings in Hilbert spaces[J]. J Math Anal Appl, 1967, 20:197. [2]OSILIKE M O. Implicit iteration process for common fixed point of a finite family of strictly pseudocontractive maps[J]. J Math Anal Appl, 2004, 294: 73. [3]OSILIKE M O,Udomene A. Demiclosedness principle and convergence results for strictly pseudo-contractive mappings of Browder-Petryshyn type[J]. J Math Ana Appl, 2001, 256: 431. [4]SU Y F, LI S H. Composite implicit iteration process for common fixed points of a finite family of strictly pseudocontractive maps[J]. J Math Anal Appl, 2006, 320: 882. [5]GU F. The new composite implicit iteration process with errors for common fixed points of a finite of strictly pseudocontractive mappings[J]. J Math Anal Appl, 2007, 329:766. [6]GU F. Implicit and explicit iterative process with errors for common fixed points of a finite family of strictly pseudocontractive mappings[J]. An St Univ Ovidius Constanta, 2010,18(1): 139. [7]XU H K, ORI M G. An implicit iterative process for nonexpansive mappings[J]. Numer Funct Anal Optimiz, 2001,22: 767. [8]张树义. 赋范线性空间中渐近拟伪压缩型映象不动点的修改的广义Ishikawa迭代逼近[J]. 应用数学学报, 2011, 34(5): 886. [9]万美玲, 张树义, 郑晓迪. 赋范线性空间中φ-强增生算子方程解的迭代收敛性[J]. 北华大学学报(自然科学版), 2016,17(3):305. [10]张树义. 一致Lipschitz渐近φi-型拟伪压缩映象多步平行迭代算法的收敛性[J]. 系统科学与数学, 2013, 33(11): 1233. [11]张树义, 赵美娜, 李丹. 渐近半压缩映象具混合型误差的迭代收敛性[J]. 北华大学学报(自然科学版), 2015, 16(3): 165. [12]ZHANG S Y. Implicit iteration approximation for a finite family of asymptotically quasi-pseudocontractive type mappings[J]. Bull Iranian Math Soc, 2014, 40 (1): 263. [13]张树义, 宋晓光. 非Lipschitz有限族集值广义渐近半压缩映象的强收敛定理[J]. 系统科学与数学, 2014, 34(9): 1051. [14]张树义, 郭新琪. 增生算子方程带误差的Noor三步迭代解与收敛率的估计[J]. 高等学校计算数学学报, 2012, 34(1): 69. [15]ZHANG S Y, SONG X G. Another note on a paper “Convergence theorem for the common solution for a finite family of φ-strongly accretive operator equations”[J]. Appl Math Comput, 2015, 258:367. [16]赵美娜,张树义, 赵亚莉. 渐近伪压缩型映象不动点的迭代逼近[J]. 数学的实践与认识, 2016, 46(15): 64. [17]张树义, 万美玲, 李丹. 渐近伪压缩型映象迭代序列的强收敛定理[J]. 江南大学学报(自然科学版), 2014, 13(6) :726. [18]SENTER H F, DOTSON W G. Approximating fixed points of nonexpansive mappings[J]. Proc Amer Math Soc, 1974, 44: 375. [19]TAN K K, XU H K. Approximating fixed points of nonexpansive by the Ishikawa iteration process[J]. J Math Anal Appl, 1993, 178: 301.
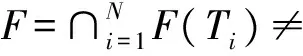
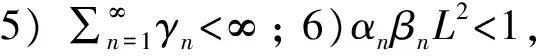
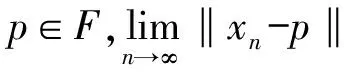
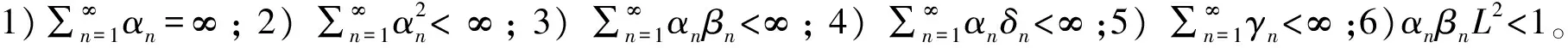
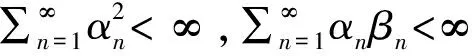
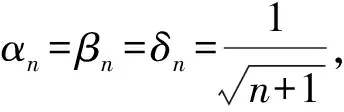
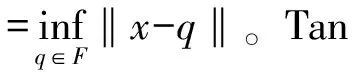
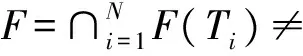
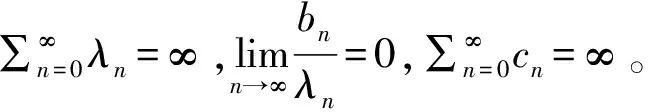
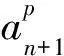
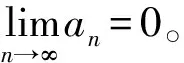
2 主要结果