太原市第三实验中学,山西太原030031 董立伟

对一个不等式的推广及加强

太原市第三实验中学,山西太原030031 董立伟

文[1]刊登了2175号问题的解答.原题如下：

设x,y,z＞0,求证：

该不等式不等号左右两侧相对应的各项均互为倒数,使得式子的形式整齐优美.原解答采用了初等的作差法,解答对求和顺序作了精心的调整,简洁巧妙.但是,配凑平方对变量的个数及指数有较强的的依赖性,这使得对问题的深入研究变得困难.本文给出了该问题的一个另证,并从证明出发,对问题作了推广与加强.

一、问题的另证

证明 由基本不等式,可得

问题得证.

由Cauchy不等式,

问题得证.

证明中我们惊喜地得到了一个加强的结果：

上述证明方法还可用来巧证问题1772.[2]原问题如下：

已知x,y,z∈R+,证明：

证明 观察左右两侧,由对称性,只需证明

二、问题的推广

罗增儒教授认为,一题多解的一大教学功能是,从多角度审视问题,有助于接近问题的深层结构.[3]

上述证明过程所用到的只有两个最基本的不等式—均值不等式和Cauchy不等式.相比于原解答,基本不等式与Cauchy不等式的成立不依赖于变量的个数.当变量个数增多时,无非是多并列几项.这使得对原不等式的推广成为可能．

推广1个数推广

对xi＞0,i=1,2,...,n,求证：

证明 先对不等式左边的各项进行变形.第一项变形如

下：

同理可得其余n-1个式子,

将上述n个式子相加可得

由上式的对称性,要证明原不等式,只需再证明

即可.即证

由Cauchy不等式,

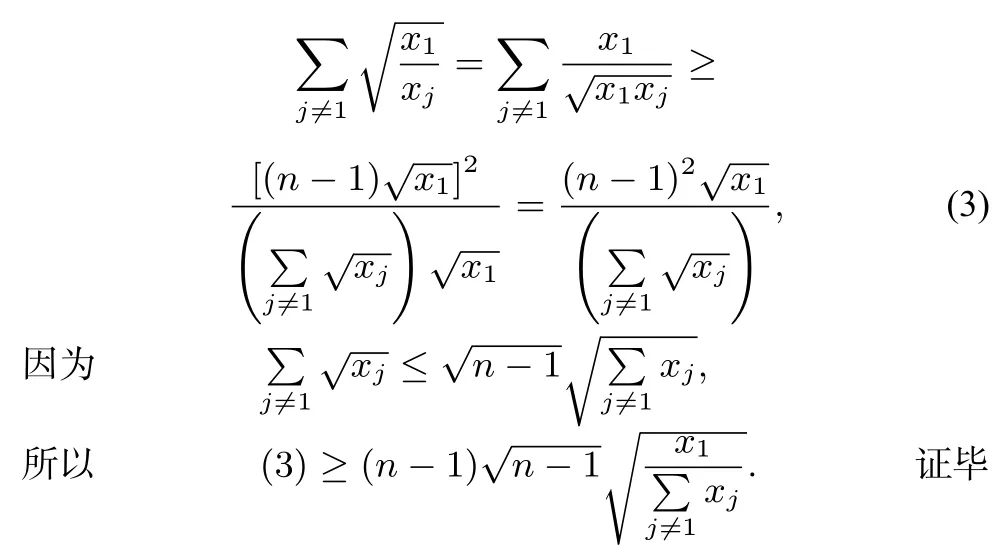
可以看到,上述证明中均值不等式及Cauchy不等式对指数与系数的依赖也是非本质的.因此,还可以推广如下.

推广2指数推广

对xi＞0,i=1,2,...,n,m≥2,m∈N+,求证：

证明 对不等式左边第一项变形,得

同理可得其余n-1个式子.由对称性,要证明原不等式,只需再证明

推广3系数推广

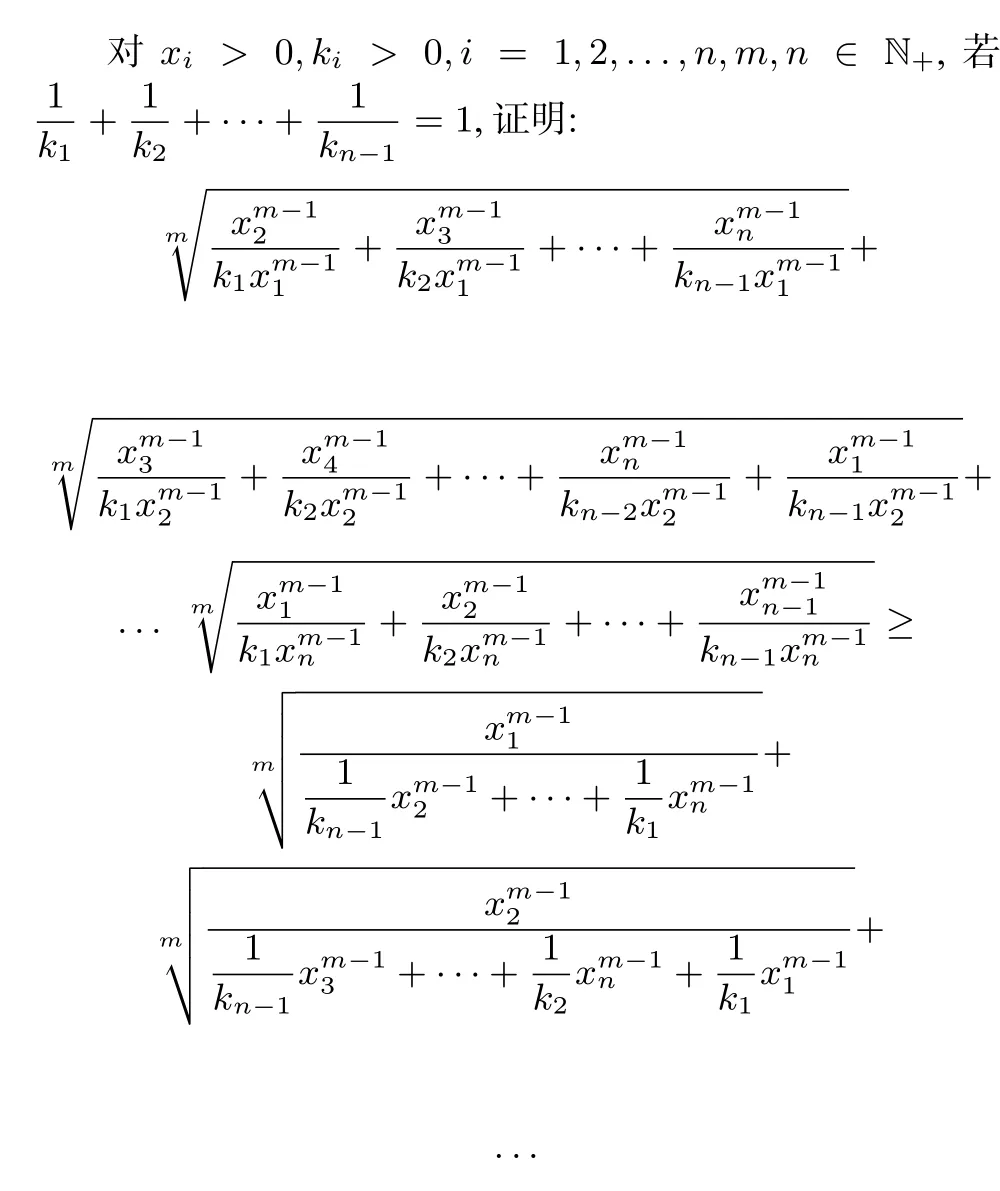
同理可得其余n-1个式子.

由对称性,只需再证明

不等式成立.

由于可以令上述不等式中xi=asi(其中i= 1,2,...,n,s为任意实数),所以,当取变量个数n和次数s为特定值时,可以得到一些推论．

推论 对a＞0,b＞0,c＞0,m∈N+,k1＞0,k2＞0,k1+k2=1,则

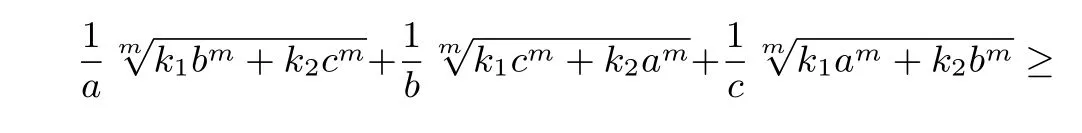
三、问题的加强

在“问题的另证”一节,我们意外得到了一个加强命题.在“问题的推广”的证明过程中发现,这一加强命题不依赖于变量个数、指数和系数,因此在三个推广命题中依旧成立(本节不再赘述).这启发笔者继续去寻求不等式的上界和下界.遗憾的是这一问题不存在上界.

下面给出推广2中命题的一个下界,其他可类似得到.

命题 对xi＞0,i=1,2,...,n,m≥2,m∈N+,

证明 对不等式中间式子的第一项变形,得

命题得证.

当命题中的m分别取2和3并约去n-1,即分别变为《数学通报》问题1403和问题1510.

四、问题的反思

研究数学问题不能仅仅把得到解答作为目的.数学问题中所蕴含的各种思想方法及解决问题的过程中所折射出的更普遍的结论会散发出更耀眼的光芒.

某一问题的解法通常不唯一.从不同的角度思考问题,通常会得到不同的解法.有些方法对各条件的依赖较强,有些则较弱.对条件依赖较弱的解法通常能更容易地触碰到问题的深层结构,从而有助于将问题加以延伸,帮助我们得到更为普遍的结论.

[1]安振平.数学问题2175解答[J].数学通报,2014,53(4)：65

[2]孙志坤.数学问题1772解答[J].数学通报,2009,48(2)：64

[3]罗增儒.高考复习要抓准方向(续)[J].中学数学教学参考(上旬), 2016(11),2-5