姜蕴芝,葛永斌

(宁夏大学 数学统计学院,宁夏 银川 750021)

求解波动方程的2种显式高精度紧致差分格式

姜蕴芝,葛永斌*

(宁夏大学 数学统计学院,宁夏 银川 750021)

针对一维波动方程，空间采用四阶Padé逼近，时间采用中心差分离散得到了一种时间二阶、空间四阶精度的显式紧致差分格式，其截断误差为O(τ2+h4).之后采用截断误差余项修正的方法对时间离散进行改进，改进后的格式的截断误差为O(τ4+τ2h2+h4)，即格式具有整体四阶精度.然后，通过Fourier方法分析了2种格式的稳定性.最后，通过数值实验验证了本格式的精确性和可靠性.

波动方程； Padé逼近； 紧致格式； 显式差分； 稳定性

波动方程是一类重要的双曲型偏微分方程，在数学、物理、化学等领域内有着广泛的应用[1].对这类方程进行数值求解的方法主要有有限差分法、有限元法和有限体积法等.就有限差分法而言，对该类问题研究的理论成果有：文献[2]采用二阶中心差分格式和非均匀网格离散，提出了一种求解一维波动方程在非均匀时间网格上的三层显式差分格式，该格式具有一阶精度；文献[3]利用泰勒级数展开及待定系数法建立了一种求解一维波动方程的三层隐格式，该格式是条件稳定的，并且具有四阶精度；文献[4]将Runge-Kutta方法应用到哈密顿系统中并与辛格式相结合，提出了求解一维波动方程的一类显式辛方法，该方法具有二阶精度，并且是条件稳定的；文献[5]采用三次样条公式推导出精度分别为O(τ2+h2)、O(τ2+h4)、O(τ4+h2)和O(τ4+h4)的4种差分格式，并采用Fourier方法分析了格式的稳定性；文献[6]对一维二阶波动方程提出了具有二阶精度的精细时程积分法，该方法能够在时间方向上精确计算，空间方向的局部截断误差为O(h2)，并且该方法是无条件稳定的；文献[7]通过加权平均和紧致差分离散的思想提出了2种精度分别为O(τ2+h4)和O(τ4+h4)的隐式紧致差分格式；文献[8]在Crank-Nicolson格式的基础上设计了重叠型区域分解的并行算法，该算法的最优逼近阶为O(τ2+h2)；文献[9]利用三次样条插值，提出了求解一维波动方程的一种三层隐式差分格式，该格式最优能够达到时间二阶，空间四阶精度，并且是无条件稳定的；文献[10]通过四次样条函数与广义梯形算法相结合的方法提出了一维波动方程的一类两层差分格式，其精度为O(τ2+h4)，当选择适当的参数时，其精度可提高到O(τ3+h4)；文献[11]采用四阶紧致差商逼近公式及加权平均思想，提出了2种精度分别为O(τ2+h4)和O(τ4+h4)的交替方向隐式格式，前者是无条件稳定的，后者是条件稳定的；文献[12]提出了一种求解一维波动方程的高精度隐式差分格式，该格式是无条件稳定的，并且具有时间二阶、空间四阶精度.本文将建立2种显式紧致差分格式，为此，考虑如下一维波动方程的初边值问题:

(1)

(2)

(3)

其中,u(x,t)是待求未知函数，a为波动系数，f(x,t)为非齐次项，φ(x)、ψ(x)、g0(t)、g1(t)为已知函数，且具有充分的光滑性.

1 显式紧致差分格式的构造

1.1 CTFS格式对初始时间层的离散.利用泰勒展开公式有

(4)

将(2)式代入(4)式中，进行整理并舍去其截断误差项有

(5)

(6)

对于空间边界节点的处理，由(1)式与(3)式可得

(7)

(8)

(9)

对上式进行整理，并舍去其截断误差项有

(10)

1.2 FTFS格式为了使时间精度与空间精度能够相匹配，使格式整体精度达到四阶，下面对上述差分格式进行改进，进一步提高时间精度，为此，对初始时间层的离散采用文献[7]中的方法，有

(11)

其中λ=τ/h.对于时间二阶导数项的离散，采用中心差分格式离散后保留其截断误差主项，可得

(12)

又由(1)式可得

(13)

将上式代入(12)式中有

(14)

对(14)式进行整理，并舍去其截断误差项有

又由(1)式，对上式进行变形有

(15)

(15)式即为整体四阶精度的显式紧致差分格式，记为FTFS格式.由格式的构造过程可知，该差分格式的截断误差为O(τ4+τ2h2+h4).

2 稳定性分析

引理 1[1]实系数二次方程μ2-bμ-c=0的根按模不大于1的充分必要条件为|b|≤1-c≤2.

对于(6)式有

(16)

对上式进行化简整理有

(17)

(18)

令Uj=(uj,vj)T，并将(17)式代入进行整理有

(19)

从而可得CTFS格式(10)的误差增长矩阵为

(20)

令λ=τ/h，r=aλ,则得上述误差增长矩阵的特征方程为

(21)

(22)

(23)

(24)

将(17)式代入(24)式进行整理，可得FTFS格式的误差增长矩阵为

(25)

则误差增长矩阵的特征方程为

(26)

其中

因此，可得该格式稳定的充要条件为

(27)

上式等价于如下2个不等式:

(28)

对于不等式(28)易得

(30)

由于不等式对任意ω的取值都要成立，所以有

(31)

对于不等式(29)，由求根公式易得其等式解为

(32)

(33)

3 数值算例

为了验证本文所提2种格式的精确性和可靠性，现考虑如下2个具有精确解的初边值问题.

问题 1[7]:

其精确解为u(x,t)=sin(πt)sin(πx).

问题 2 :

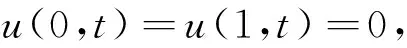
其精确解为u(x,t)=te-πtsin(πx).

表1～3给出了问题1的计算结果.表1采用本文CTFS格式与文献[7]中的四阶格式进行了计算.由于这2种格式的精度均为时间二阶、空间四阶，因此取τ=2h2，计算了t=0.5时刻取不同h时(τ也相应不同)的L∞和L2范数误差和收敛阶.eL∞和eL2范数及收敛阶的定义如下：

(34)

(35)

(36)

由表1的数据可以看出，2种格式空间均达到了四阶精度，而本文的CTFS格式要比文献[7]中的四阶格式更为精确.表2给出了本文FTFS格式和文献[7]中的四阶格式的计算结果，由于2种格式均具有整体四阶精度，因此取τ=h，计算了t=0.5时刻取不同h时的L∞和L2范数误差和收敛阶.可以看出，2种格式几乎具有相同的精度.

因此，当|a|λ大过1之后，计算结果是发散的.

表1 问题1当τ=2h2时，在t=0.5时刻对不同h的L2和L∞范数误差及收敛阶Table 1 The L2,L∞ norm error and the convergence rate with τ=2h2 at t=0.5 for different h for Problem 1

注:1.46E-3=1.46×10-3，下同.

表2 问题1当τ=h时，在t=0.5时刻对不同h的L2和L∞范数误差及收敛阶Table 2 The L2,L∞ norm error and the convergence rate with τ=h at t=0.5 for different h for Problem 1

表3 问题1当h=1/32时，对不同λ的L∞范数误差Table 3 The L∞ norm error with h=1/32 for different λ for Problem 1

表4～6给出了问题2的计算结果.

表4 问题2当τ=h2时，在t=1时刻对不同h的L2和L∞范数误差及收敛阶Table 4 The L2,L∞ norm error and the convergence rate with τ=h2 at t=1 for different h for Problem 2

表5 问题2当τ=h时，在t=1时刻对不同h的L2和L∞范数误差及收敛阶Table 5 The L2,L∞ norm error and the convergence rate with τ=h at t=1 for different h for Problem 2

表6 问题2当h=1/32时，对不同λ的L∞范数误差Table 6 The L∞ norm error with h=1/32 for different λ for Problem 2

4 结论

致谢 宁夏大学自然科学基金项目(ZR1407)和宁夏大学研究生创新项目(GIP2016032)对本文给予了资助,谨致谢意.

[1] 戴嘉尊,邱建贤.偏微分方程数值解法[M].南京:东南大学出版社,2002.

[2] CHO C H.Stability for the finite difference schemes of the linear wave equation with nonuniform time meshes[J].Num Meth Part Diff Eqns,2013,29(3):1031-1042.

[3] 张天德,孙传灼.关于波动方程的差分格式[J].山东工业大学学报,1995,25(3):283-287.

[4] 孙耿.波动方程的一类显式辛格式[J].计算数学,1997,19(1):1-10.

[5] 齐远节,刘利斌.求解二阶波动方程的三次样条差分方法[J].大学数学,2011,27(1):59-64.

[6] 金承日,吕万金.二阶双曲型方程的精细时程积分法[J].计算力学学报,2003,20(1):113-115.

[7] 葛永斌,朱琳,田振夫.求解波动方程的高精度紧致隐式差分方法[J].宁夏大学学报(自然科学版),2005,26(4):297-299.

[8] 田敏,羊丹平.波动方程的重叠型区域分解并行有限差分算法[J].山东大学学报(理学版),2007,42(2):28-38.

[9] RASHIDINIA J,JALILIAN R,KAZEMI V.Spline methods for the solutions of hyperbolic equations[J].Appl Math Comput,2007,190(1):882-886.

[10] LIU T,LIU L,XU H,et al.A new two level difference scheme for solving one-dimensional second-order hyperbolic equations[C]//2012 Fifth International Joint Conference on Computational Sciences and Optimization,2010:218-221.

[11] 马月珍,李小刚,葛永斌.二维波动方程的高精度交替方向隐式方法[J].四川师范大学学报(自然科学版),2010,33(2):179-183.

[12] 崔进,吴宏伟.一类波动方程初边值问题的高阶差分格式[J].应用数学,2014,27(1):166-174.

[13] LELE S K.Compact finite difference schemes with spectral-like resolution[J].J Comput Phys,1992,103(1):16-42.

[14] 葛永斌,吴文权,田振夫.二维波动方程的高精度隐格式及其多重网格算法[J].厦门大学学报(自然科学版),2003,42(6):691-696.

[15] 余跃玉.一种Caputo型时间分数阶波动方程的差分方法[J].四川师范大学学报(自然科学版),2014,37(4):524-528.

2010 MSC：35A35; 65M99

(编辑 陶志宁)

Two Kinds of Explicit High Order Compact Difference Schemes for Solving Wave Equations

JIANG Yunzhi,GE Yongbin

(CollegeofSchoolofMathematicalandStatistics,NingxiaUniversity,Yinchuan750021,Ningxia)

In this paper,an explicit compact difference scheme is obtained for solving the one dimensional wave equation.The truncation error of the scheme isO(τ2+h4).It’s constructed by applying the fourth-order accurate Padé approximation in space and the second-order accurate central difference in time.Then,the remainder of the truncation error correction method is employed to improve the accuracy of the discretization of time,the truncation error of the improved scheme isO(τ4+τ2h2+h4),which means the scheme has an overall fourth-order accuracy.And then,the stability conditions of the two schemes are obtained by the Fourier method.Finally,the accuracy and the reliability of the present two schemes are verified by numerical experiments.

wave equation; Padéapproximation; compact scheme; explicit difference; stability

2015-01-16

国家自然科学基金(11361045)

O242.1

A

1001-8395(2017)02-0177-07

10.3969/j.issn.1001-8395.2017.02.006

*通信作者简介：葛永斌(1975—),男,教授,主要从事偏微分方程数值解法和计算流体力学的研究,E-mail:gyb@nxu.edu.cn