高考数学试题对高三复习的启示*

☉厦门大学附属实验中学 林运来

一、问题提出

在大力倡导创新教育的形势下，数学教育正经历从“双基”到“三维目标”直至今日“核心素养”的转型和跨越.相应地，高考试题命题范式已经经历了政治立意、知识立意、能力立意三个阶段，以后的命题趋势必转化为素养立意［1］.钟启泉先生指出，新的学力概念——“核心素养”意味着课堂的根本转型，从“知识传递”到“知识建构”的转型.教学中，教师需要思考如何在数学思维能力和创新意识方面“补钙”.在高考备考复习中，如何才能最大限度地提高课堂教学的有效性，让学生掌握数学知识的本质，领悟数学思想方法的精髓，提升数学思维品质，提高数学素养，确是一个值得探索与急需解决的问题.

相同的知识内容，相同的能力要求，在不同年份的高考中从不同的角度和形式进行考查，这就需要学生有更开阔的视野和思维，也为高三数学复习角度的多元化、立体化提出了新的要求.当我们仔细去研读新课程高考下的试题，总会有不一样的发现，总会给我们的教学带来思考.如果只是去关注这些题目的解法考查的知识，将会使我们错过它们带给我们的精彩和对教学的启示.

二、高三复习“新”角度

1.从“联系”的角度拓展教学

例1（2016年高考全国卷Ⅰ文科第5题）直线l经过椭圆的一个顶点和一个焦点，若椭圆中心到l的距离为其短轴长的，则该椭圆的离心率为（）.

解法2：如图1，|OB|为椭圆中心到l的距离，则|OA|·|OF|=|AF|·|OB|，即bc=a·，

图1

解法3：如图1，|OB|为椭圆中心到l的距离，即|OB|=所以∠OAB=30°，在Rt△OAF中，|OF|=|AF|，即c=a，所以e=.故选B.

方法1从代数角度寻求a与c的关系，方法2利用等面积法得出a与c的关系，方法3根据“已知条件集中于椭圆的特征△OAF”（三边长分别为a，b，c）这一特点，转化为求∠OAF的大小，从而快速解决问题.

图2

解析：不少学生看到直线与椭圆相交就联立方程组，陷入符号运算的泥潭，不能自拔，无功而返.事实上，若注意到直线的斜率为，可得直线的倾斜角等于60°，画出椭圆的“焦点△MF1F2”，如图2，则椭圆的离心率这一解法刻画出问题最本质的几何关系，是对椭圆定义的灵活使用.可见，概念就是本质！命题人对学生“观察发现，多思少算”的思维品质的考查是刻意为之.

中学数学知识的联系比较紧密，数学知识的考查也注重相关知识之间的综合考查，这就要求教师在高三复习教学中对相关联的知识进行拓展，有效引导学生构建知识网络.以上两题涉及“椭圆离心率”知识的综合，教学时可以围绕求椭圆离心率的方法引导学生构建如下的思维导图：

2.从“变式”的角度深化教学

例3（2008年高考江苏卷第13题）满足条件AB=2，AC=BC的三角形ABC的面积的最大值为______.

解析：本题的常规解法是利用解三角形的知识，建立△ABC的面积关于边长BC的函数，进而转化为函数的最值问题.若考虑到此题的几何背景——阿波罗尼奥斯圆，利用数形结合思想，充分发挥“形的直观”（AB是定长，问题转化为求动点C到直线AB距离的最大值）与“数的精确”（通过建立直角坐标系，求出动点C的轨迹方程）两方面的优势，问题便能快速获解.这样解题把握了题目的本质，也揭示了题目的真面目.

本题还有很大的变式空间.如针对动点的轨迹类型，教师可以通过搭建螺旋式上升的变式题这个“脚手架”，设计一串变式，“一网打尽”式地进行展示、解决题型.该形式能大大节约讲解时间，并提高效率，新课和复习课都适用，也适用于试卷讲评课中作为思考题留给学生［2］.比如［3］：

变题1满足条件AB=2，周长为8的△ABC面积的最大值为______（.答案：2）

变题4在△ABC中，若a=2，b-c=1，△ABC的面积为

变题5（2013年高考江苏卷第17题）在平面直角坐标系xOy中，点A（0，3），直线l：y=2x-4.设圆C的半径为1，圆心在l上，若圆C上存在点M，使MA=2MO，求圆心C的横坐标a的取值范围

这样就有助于揭示此题内隐的知识链，看清题目的来龙去脉，从而把握问题的本质.

3.从“创新”的角度思考问题

在国家倡导“大众创业、万众创新”的背景下，“创新”无疑将成为教育领域关注的热点.数学学科对培养学生的创新能力具有不可推卸的责任.教育最终的目的是培养人才，特别是培养和造就高素质的创造性的人才.教育系统应当为推动大众创业、万众创新提供人才支撑.在考试中凸显对创新能力的要求，不仅符合社会对人才选拔的核心要求，也是数学时代性和实践性的应有之意.一般来说，高考中往往通过设置综合性、开放性、探索性试题，考查学生的创新意识和探究精神［4］.

例4（2015年高考全国卷Ⅰ理科第16题）在平面四边形ABCD中，∠A=∠B=∠C=75°，BC=2，则AB的取值范围是______.

解析：此题注重考查学生的思维能力和创新意识，计算不可或缺，但是更注重对学生的数学思想方法的考查.题目中的动点D具有无限性的特征，若立足于有限与无限思想，可以考虑运用极限化策略进行解答.当D→A时，∠B=∠C=75°，∠A=30°，由正弦定理易求得AB=；当D→C时，∠A=∠B=75°，∠C=30°，由正弦定理易求得AB=，从而AB的取值范围是

高考中，对于较难的问题，经常需要“感性分析”和“直觉判断”，常见的题型是小题和探究性的解答题.上述分析过程将解三角形的知识和极限思想很好地结合在一起，通过对问题的特殊认识形成特殊的解法（极限法），体现出“考数学思想方法而不是考知识记忆、考数学素养而不是考模式套路”的特点.数学背景的新颖才可以真实地检测应用数学知识、思想解决问题的水平，体现真正的数学素养的差异［1］.

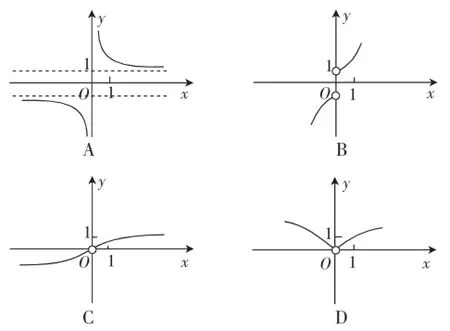
解析：一些考生看到判断函数图像问题，立即想到利用导数知识进行解答，陷入“大运动量”的计算困境.若注意到函数的定义域为｛x|x≠0｝，当x→0+时→+∞，可排除B、C、D三项，应选A.利用极限思想解答既快捷又准确，几乎不用任何计算就能得出正确选项，显示出命题者对数学本质的执著追求.

变题2（2013年日本早稻田大学入学试题）给定抛物线C：y2=4px（p＞0），焦点F（p，0）.设过焦点F且相互垂直的两条直线l1，l2，曲线C与l1交于点P1，P2，与l2交于点Q1，Q2.

（1）设直线l1的方程为x=ay+p，点P1，P2相应坐标为（x1，y1），（x2，y2），试用a，p表示y1+y2，y1y2；

（2）证明：无论如何取直线l1，l2，都是一个常数.

在解答第（2）问时可以先“遥望”一下问题的结果.当直线l1垂直于x轴时，直线l2就是x轴，此时线段P1P2是抛物线的通径，Q1，Q2中的一个点为坐标原点，另一个点为“无穷远点”，即|P1P2|=4p，|Q1Q2|→∞，则，因此需要证明无论如何取直线l，l12都是常数，这就为解题指明了方向.一个有科学素养的人，在研究一个问题的时候，第一件事就是遥望一下这个问题的结果！问题研究的过程，从来都是“大胆猜想、小心证明”的过程［5］.

4.从“素养”的角度回归本真

即将颁布的“课程标准”中明确了中学数学的6个核心素养：数学抽象，逻辑推理，数学建模，数学运算，直观想象，数据分析.根据现行的课程标准下的高考，也可以看出以上核心素养的影子［1］.哈尔莫斯认为，具备一定的数学修养比具备一定的量的数学知识更重要.教师在强调解题的同时更应该注重课堂教学的思想性，注重学生数学素养的提高［6］.

在高三复习教学中，把简约出的时间和空间还给学生，教师要善于变“习题”为“问题”，变“问题”为“课题”，变“讲授”为“悟道”，让学生的学习更主动、更自由，学生通过自己的思考、探究、揣摩，悟出数学学习之道，提高学科素养.经验告诉我们，有时教师讲得越多，学生越不明白，而让学生自悟自得，效果会更好，这需要教师通过非常巧妙、到位的设计和智慧的引导，回归数学教育的本真——为发展学生的核心素养而教.

A.（-2，0）B.（-3，0）C.（-4，0）D.（-5，0）

这是我校高三月考选择题最后一题，讲解后，笔者进一步提出一些问题引导学生思考.教学过程如下：

师：这道题是在“左特征点”这一“新定义”包装下的定点问题.近年来，定值定点问题是高考和竞赛的一个热点，其解法充分体现了解析几何的基本思想：运用坐标法逐步将题目条件转化为数学关系式，然后综合运用代数、几何知识化简求值.解答此类问题要大胆设参，运算推理到最后参数必消，定点、定值自然显露.观察发现此题的结论非常优美，这难道是巧合吗？是否还有更一般的规律有待我们去发现？这些问题促使我们去思考、联想.大家不妨研究一下，看有什么收获？学生很快探究得出：

师（追问）：此时一个自然的想法是，若弦AB不是经过椭圆的左焦点F，而是经过x轴上的某个定点N（t，0），在x轴上是否存在定点M，使得MN平分∠AMB呢？

师：结论2给我们的一个“信息”就是“定点M的坐标与椭圆方程中的b2无关”，而在椭圆+=1（a＞b＞0）中，只需把b2换成（bi）（2其中i是虚数单位），就得到双曲线C：-=1（a＞0，b＞0），于是可以大胆猜想：

学生进一步探究得到：

学生证明结论3后，笔者进一步追问：椭圆、双曲线、抛物线都是圆锥曲线，对比椭圆、双曲线，上述的结论对抛物线还成立吗？

学生探究得到：

结论4过定点N（t，0）（t≠0）作抛物线C：y2=2px（p＞0）的一条与x轴不垂直的弦AB，则存在定点M（-t，0），使得MN平分∠AMB.

最后，笔者展示下面的高考题：

例6（2015年高考全国卷Ⅰ理科第20题）在直角坐标系xOy中，曲线C：y=与直线l：y=kx+a（a＞0）交于M，N两点.

（1）当k=0，分别求C在点M和N处的切线方程；

（2）y轴上是否存在点P，使得当k变动时，总有∠OPM=∠OPN？说明理由.

师：不难发现结论4与这道高考题的第（2）问“如出一辙”.例6难度不大，但内涵丰富.解答后，提出一些问题供大家课后探究.如：可以从结论入手，继续向下追问；也可以反思题目的条件，寻求问题的本源；还可以进行更深层次、更多元的思考：证明两个角相等有哪些方法？题目的结论反过来成立吗？题目的背景换成椭圆，或双曲线，结论还成立吗？……

这些有意义有价值的开放性问题，不仅有助于创造自主探究与发现的机会，培养学生终身受益的学习习惯和思维方法，也为教学提供了丰富的素材［4］.上述教学中，教师本着“夯实基础、激发兴趣、着眼高考、适当提高”的原则，利用问题引导学生在简单整齐的数学美的驱动下，通过对问题的结论产生联想，进而提出猜想，通过证明猜想，得出新的结论，从而把握问题的本质.这正是数学研究的一种基本套路.

数学大师华罗庚说过：“独立思考能力是科学研究和创造发明的一项必备才能.”数学活动经验的积累是提高学生数学素养的重要标志，在积累数学活动经验的过程中，教师要根据学生的“最近发展区”创设问题情境，让每一个学生领到合适的任务，在问题驱动下进行学习，“跳一跳，够得着”，实实在在地做一些事情，使学生回到真实环境中去积极体验和感受新知的构建过程.

三、结束语

罗增儒教授指出：我们可以通过有限的典型考题的学习，去理解那种解无限道题的数学机智.对学生来说，学会考试也是核心素养的一部分，但品格和学习能力的培养才是终极要求，知识只是抓手.教师课堂上的任务则是透过书本知识，引导学生发现隐藏在知识背后的深刻思想，这才是真正的教育［6］.

正因为如此，我们才更要培养学生适应未来的能力而非“填充”当前的知识.对数学学习而言，掌握学习的策略与方法，以数学思想为课程，拥有学以致用的方法，将知识与生活实际相联系，才能充分体现“能独立思考，体会数学的基本思想和思维方式”的目标要求.高三数学复习教学要在注重常规复习的基础上，根据考查的要求及方向探索不同的教学角度，促进学生对知识的理解和掌握，培养学生从不同的角度思考和解决问题的能力，从而提升数学核心素养.

1.朱伟义，曹凤山.忽如一夜春风来素养之花遍地开——从高中数学核心素养的视角看2016年浙江高考数学试题［J］.中学数学（上），2016（9）.

2.俞新龙.数学教师要尽快学会用变式教学［J］.数学通讯（下），2015（10）.

3.刘鸿春.轨迹问题的命题新趋向［J］.数学通讯（下），2016（7）.

4.林运来，杜锟.注重核心素养，引领数学改革——2013～2016年高考数学全国课标卷试题综述［J］.中学数学教学参考（上），2016（10）.

5.王雅琪.高观点下的北京高考解析几何试题［J］.数学通报，2016（11）.

6.曹广福.数学课程标准、教材与课堂教学浅议［J］.课程·教材·教法，2016（4）.

2015年度漳州市基础教育课程教学研究重点课题——《全国高考统一命题后高中数学教学的调整和优化对策研究》（ZPKTZ15008）研究成果.