冯云青,侯磊,2

(1.上海大学数学系,上海200444;2.上海高校计算科学E-研究院,上海200030)

构造高阶插值函数求解表面冲击碰撞问题

冯云青1,侯磊1,2

(1.上海大学数学系,上海200444;2.上海高校计算科学E-研究院,上海200030)

本文主要采用Lagrange双三次形函数来构造插值函数,从而利用有限元方法求解表面冲击碰撞问题中的耦合方程组.为了避免龙格现象,采用Lobatto点构造插值节点.本文不仅采用高阶的形函数,也使用两种不同的数值积分方法,结合这两点,从而提高数值解的精度.根据以上的理论分析结果,本中使用Matlab编程模拟发生碰撞时材料的形变和应力变化.

有限元;Lagrange;正交积分

0 引言

汽车电子化的飞速发展,对汽车产业的相关研究带来了前所未有的现代化冲击.由于汽车结构发展的多样性和复杂性,维修设备的现代化发展,汽车修复技术需要变革.为了能更好地变革修复技术,进而对研究汽车碰撞的模拟实验也提出了更多样性的模拟和更好的仿真效果要求.因此,汽车碰撞问题以及修复工作的研究越来越需要高技术的引入.目前对于汽车碰撞试验的数据主要来源于实验室实物模拟与模型数值计算结合.采用数学模型与高性能计算来虚拟化试验,受到了广泛的关注.本文主要研究汽车碰撞安全相关问题,以高速碰撞时接触表面的形变与应力分布为主要研究对象,模拟实物高速碰撞后,复杂接触表面的形态.在汽车制造的材料选择中,蜂窝多孔材料由于其质量轻、抗压抗弯性能高而受到广泛关注,但这种材料微观结构复杂,材料性质各异,导致对其的数值模拟困难重重.本文试图采用非线性流固耦合方程组,对蜂窝多孔材料所构建的复杂接触表面进行数值模拟.该流固耦合方程组[1-2]为：

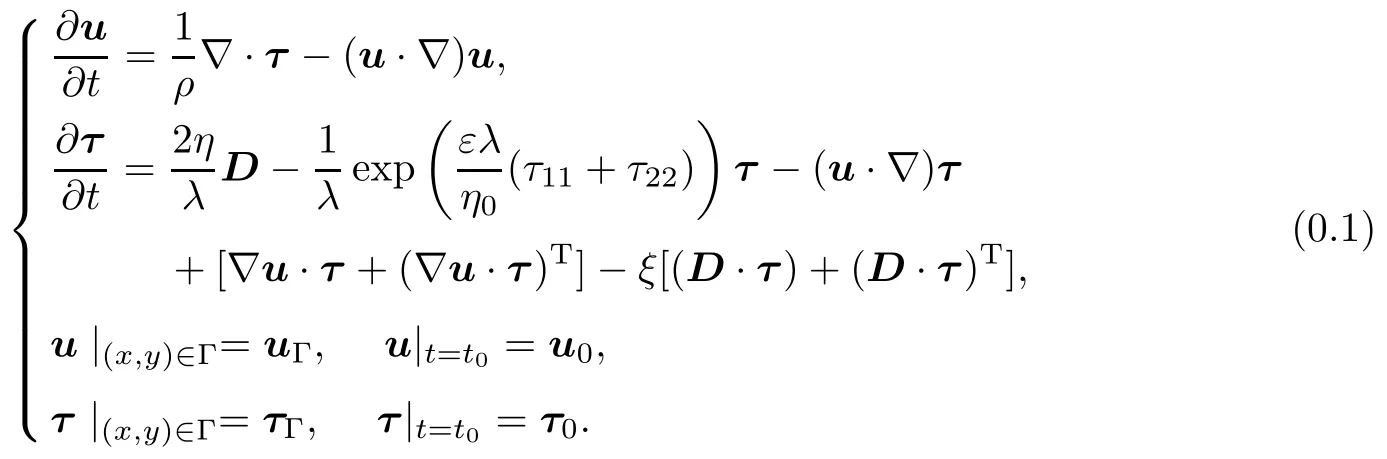
其中ρ是流体密度,ξ是切变因子,η是粘度,λ是松弛因子.该耦合方程是建立在高速碰撞的条件下,固体材料在一段时间内发生了巨大形变,因此认为它同时具有了流体性质.耦合方程组的第一式是Cauchy守恒方程,用于计算受到巨大冲击时应力场τ分布产生的弹塑性材料大变形,该变形由速度场u描述.第二式是P-T/T方程,用它来描述粘弹塑性材料应力变化时复杂接触表面的外延和简单剪切速率的阻力.P-T/T是建立在Maxwell方程[2-4]的基础上的具有瞬时拉伸特征的应力计算方程.

本文采用有限元和有限差分相结合的方式求解该流固耦合方程组,对于空间变量采用有限元方法进行离散,再用三种差分方法对时间变量进行离散,最终得到大型线性方程组[1,5-6].在对空间变量采用有限元方法离散时,引入高阶的形函数——Lagrange双三次形函数来构造插值函数,避免单元出现过于刚化的现象,从而减小了空间有限元离散所带来的误差.同时,当插值函数的阶数提高后,为了避免可能出现的龙格现象,本文用Lobatto多项式构造不等距的插值节点,且在文章[1]的基础上加入更多的插值节点使网格剖分更细,从而进一步提高有限元解的精度.在具体计算单元刚度矩阵时,由于被积函数的复杂性,需要引入积分点进行数值积分,选用较少的积分点数是另一种克服单元刚化的手段.本文是采用Gauss和Gauss-Lobatto两种积分点进行数值积分.对于积分点数的选择是有要求的,若采用过多的Gauss或Gauss-Lobatto点求积,单元刚度矩阵会因为过度刚性而变得更加糟糕,因为附加的Gauss或Gauss-Lobatto点捕捉的是刚度矩阵更高次的项.这些高次项能抵抗低次项所不能抵抗的变形,因而使单元变得刚性化.同时,更多点的积分也增加了计算量.除此以外,刚度矩阵的高精度经常导致有限元解的低精度[7].然而,若用太少的Gauss或Gauss-Lobatto点可能导致更坏结果,产生不稳定性等等.因而在有限元问题中,一个单元的最佳积分法则往往也是值得思考和探索的.文本由于对每个单元用矩形剖分后有4×4个插值节点,为此分别采用3×3和4×4个Gauss点,4×4个Gauss-Lobatto点在每个单元上进行数值积分[8-9].

1 形函数的构造

为了提高有限元解的收敛速度或减小有限元解的误差,通常采用两种方式,一种是适当提高单元形函数中多项式阶数,另一种是采用更精细的单元网格来提高有限元结果的精度.构造恰当的有限元插值函数的第一步是确定插值节点.本文采用Lobatto多项式的零点作为插值节点,构造Lagrange16点双三次多项式形函数.由于插值形函数阶数的提高,本文为避免插值函数出现震荡即龙格现象,采用不等距的插值节点.

首先考虑在区间[-h,h]上的Lobatto多项式序列[10]为：

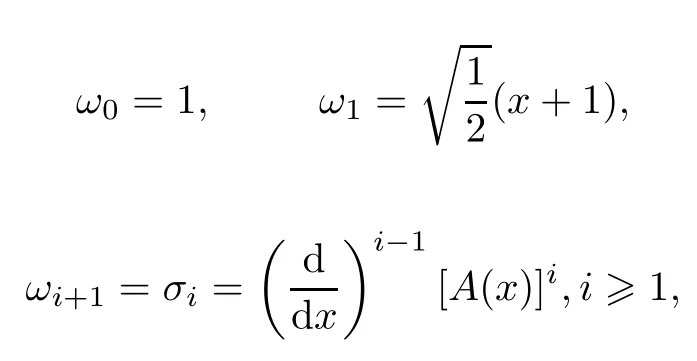
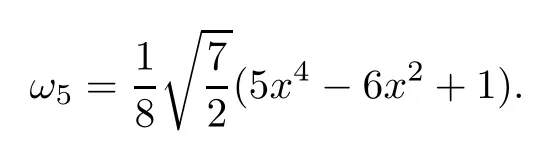
由此得到该多项式的零点为：

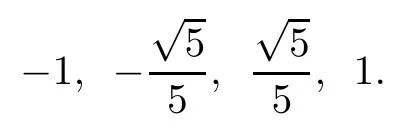
本文下面考虑的问题都是在标准元素[-1,1]×[-1,1]的矩形区域上的.将该矩形区域四等分为2×2个单元,记为单元①、单元②、单元③、单元④.再利用以上求得的Lobatto多项式的零点作为插值节点做矩形剖分,可得到每个单元上的不等距插值节点为4×4个.再对节点进行编号,如图1.1,首先对每个单元上的16个节点进行局部编号,它们的编号称为节点的局部编码.如图1.2,其次对区域内所有的插值节点按照节约内存的方式进行总体编号,这样的编号称为节点的总体编码[1,10].

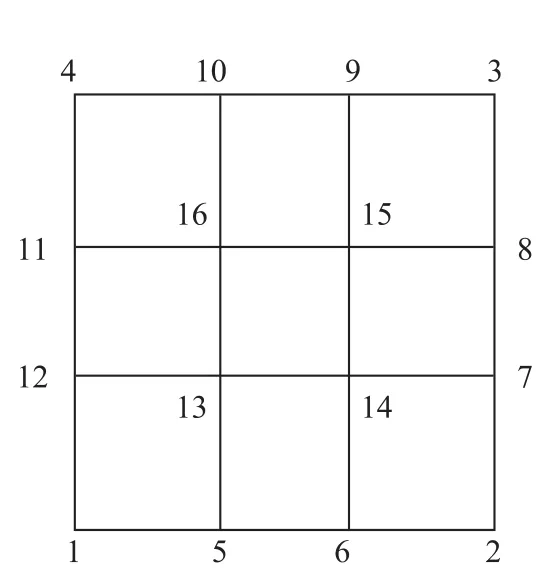
图1 .1 单元网格插值节点编号Fig.1.1 The number of interpolation nodes of element mesh

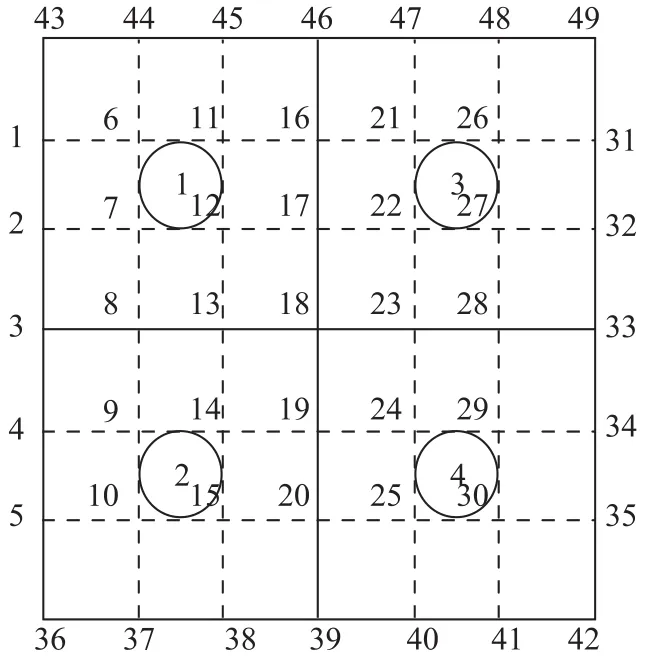
图1 .2 总体网格插值节点编号Fig.1.2 The number of interpolation nodes of global mesh

编码完成后,可列出构造方程离散格式所需要的Lagrange16点双三次形函数.可知在区间[-1,1]上的Lobatto多项式有4个零点,则一维的Lagrange形函数构造如下：

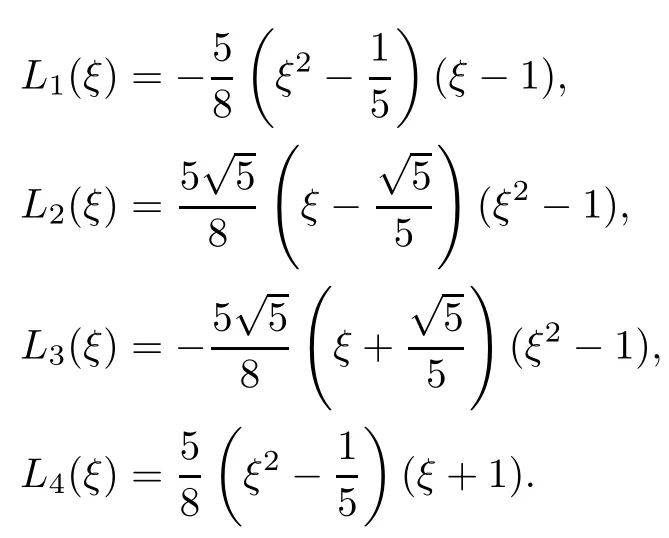
由此可得二维上的Lagrange16点双三次形函数,表示为：

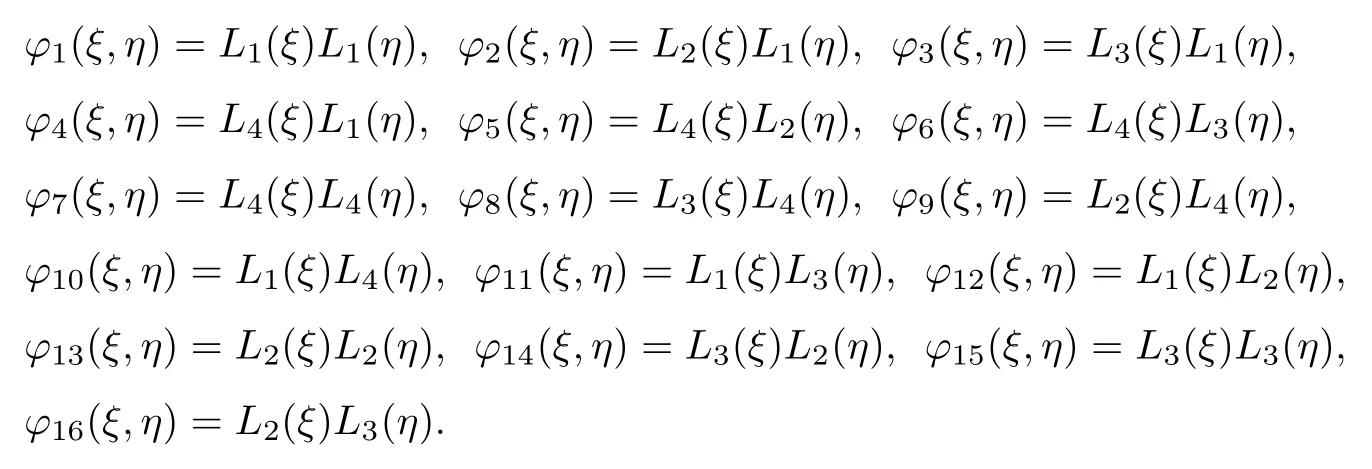
其中Li(η)也是一维Lagrange形函数.

本文在每个单元上利用16个Lobatto插值节点形成单元刚度矩阵,然后再将单元刚度矩阵合成总刚矩阵.由上面的剖分可以得到总刚矩阵为49×49矩阵.刚度矩阵的计算跟选取的有限元形函数有关.基于位移的有限元法可能存在单元出现过于刚化的现象,为了克服这一现象,可采用高阶的形函数.本文构造的是Lagrange16点双三次形函数.单元内任一点的位移是由假定的形函数及单元结点位移插值得到.通常高阶单元比低阶单元更加光滑,因为高阶单元采用更高阶的形函数,其变形更光滑,相当于外加给单元的约束变少了.这里具体的刚度矩阵的计算是用Matlab编写程序实现的,可参考后面的数值结果.

2 耦合方程组的离散

本节将对流固耦合方程组(0.1)进行有限元——有限差分离散.设方程组(0.1)中, u=iu1(x,y;t)+ju2(x,y;t)为速度场(矢量),其中的u1(x,y;t),u2(x,y;t)分别为速度u的x分量和y分量；为应力场(张量),其中的τ11(x,y;t),τ12(x,y;t), τ21(x,y;t),τ22(x,y;t)分别为应力τ对应的四个分量并且τ12(x,y;t)=τ21(x,y;t).故该耦合方程组实际上包含五个分量方程.将耦合方程组(0.1)按上述五个分量展开得到五个分量方程为：

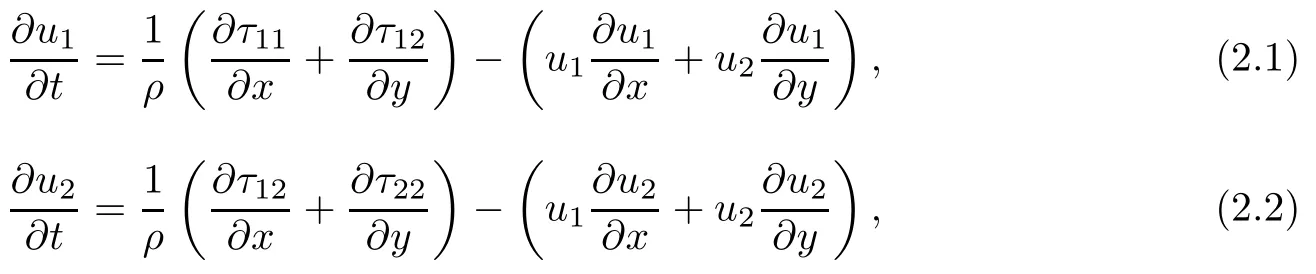
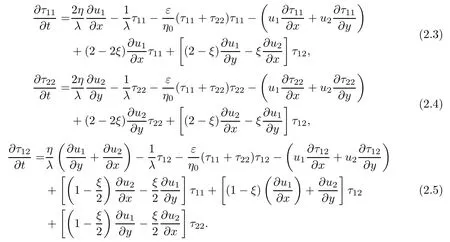
对于要计算出的u,τ且u∈H,τ∈H,其求解是有困难的.通常做法是将原问题(0.1)转化为积分形式,降低解对光滑性的要求,此时积分形式对应的解称为广义解并称广义解所在的空间为容许空间.再选取容许空间的有限维子空间,在该子空间内对广义解进一步逼近.故本文选取容许空间H的有限维子空间Vh∈H为：

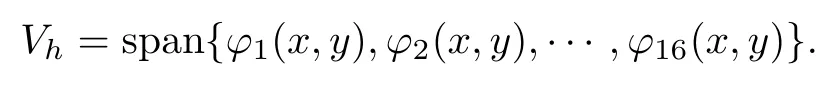
称这样的Vh为检验空间,其中ϕm(x,y)(m=1,2,···,16)为检验函数空间的基,各ϕm(x,y)在标准网格上的表达形式同ϕm(ξ,η).此时H被检验空间Vh所替代,问题转化为求近似解使得

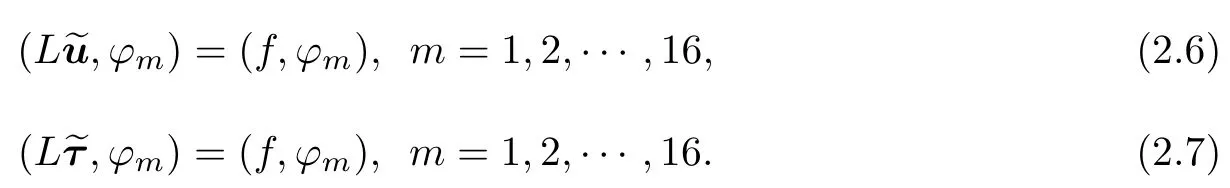
其中,L为对应耦合方程组(0.1)的微分算子.进一步,使用有限元方法,将这一过程模块化,且确保解的存在唯一性.

下文对空间变量(x,y)以及时间变量t分开处理.对于以上五个方程的空间变量,采用有限元方法进行离散.以下均是在标准网格e=[-1,1]×[-1,1]上,采用Lagrange16点双三次形函数,实现的空间有限元半离散过程.这里相当于推导了在一个单元上的空间变量的离散过程,写出的刚度矩阵均为标准网格下的单元刚度矩阵,本文中共有四个这样的单元,如图1.2,一共有49个总体编码.作者在用Matlab编写时,将标准网格上的离散结果通过坐标变换推导到实际的四个单元上,需要将节点的局部编码和总体节点编码进行转换,再将每个单元的刚度矩阵合成总体刚度矩阵.

令u1(xm,ym;tn)表示当t=tn时,速度场的x分量在该节点上的数值.同理可推得其他分量,这里不一一列举.令为以ϕm为插值基的函数,有限元解的插值基函数表达式为：

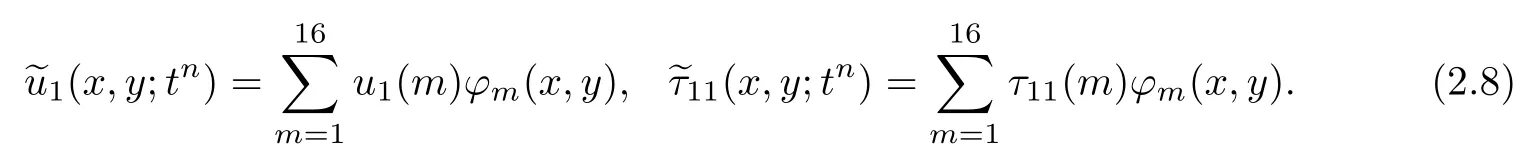
其他同理可得.

插值基函数的偏导数可表示为：

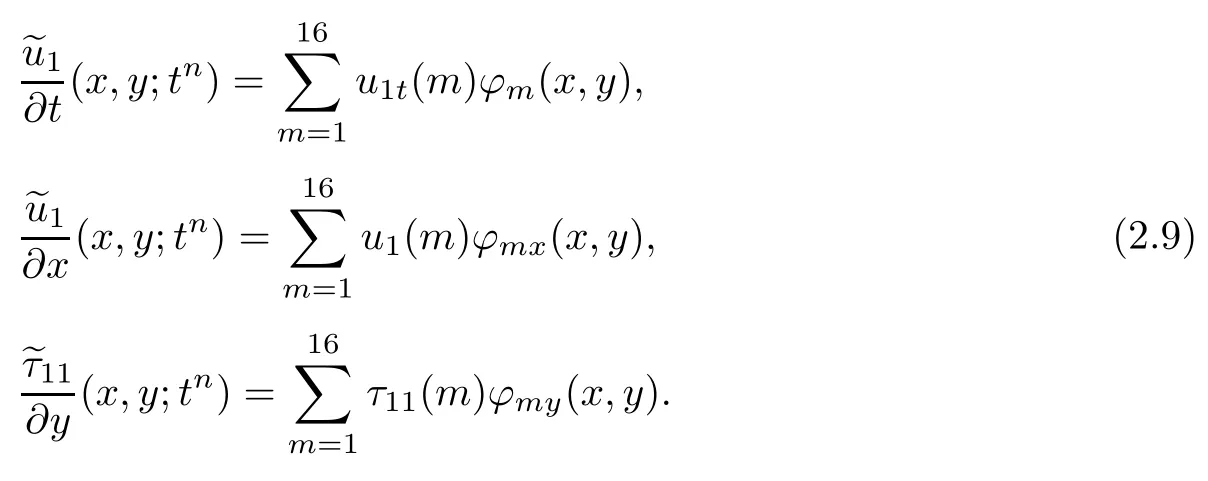
其他也同理可得.

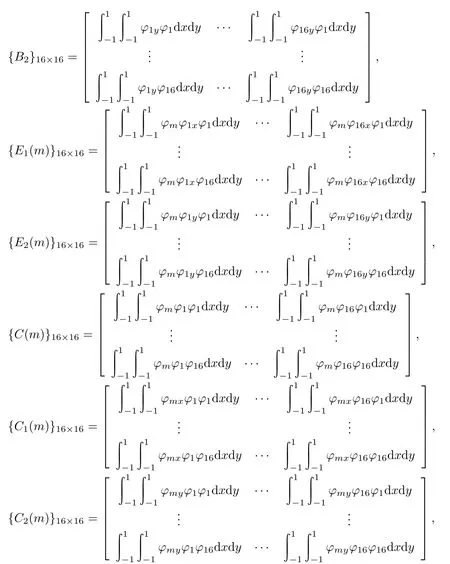
其中ϕmx、ϕmy分别表示对ϕm求x、y方向的偏导.式子(2.10)—(2.14)分别对应(2.1)—(2.5)五个方程的半离散,是对空间变量的有限元离散.需要注意的是,这里是定义在标准网格上的一个单元的离散过程.

对于时间变量的离散,本文采用三种差分方法[1,5].这里仅以方程(2.1)半离散后的有限元格式(2.10)为例,给出三种时间差分方法的全离散过程.先将半离散格式(2.10)改写为：

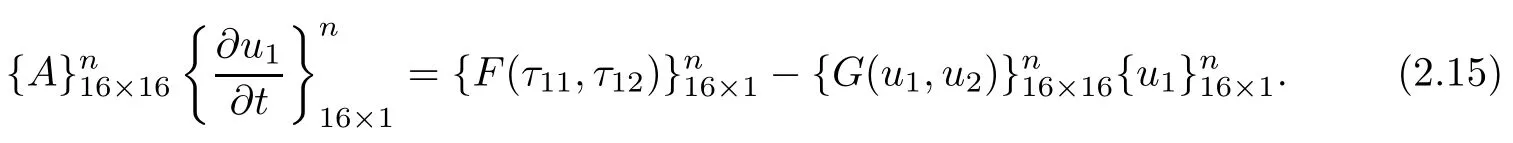
推导出对应的Euler格式为：

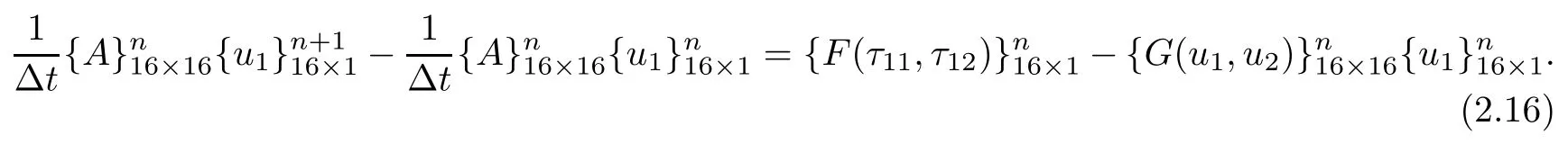
对应的半隐式Crank-Nicolson格式为：

对应的Adams二步显格式为：

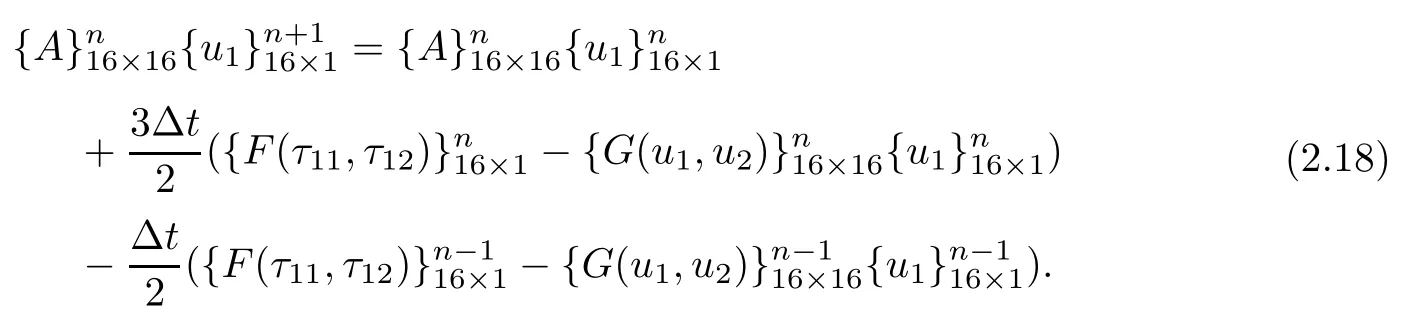
由此,方程(2.1)的空间变量和时间变量均被离散,得到了三种不同的全离散格式.其余四个方程,均可按照这三种差分格式全离散,不再赘述.三种全离散格式的程序设计见第4节.

3 Gauss-Lobatto数值积分

由第2节可以看出,在对刚度矩阵的计算中被积函数是较为复杂的,因此求其积分需要采用数值积分的方法.本文采用Gauss和Gauss-Lobatto型两种求积方法,Gauss-Lobatto求积公式与Gauss求积公式的区别在于其要求被积区间的两个端点均固定,因此所有积分点中的端点都被预先固定.众所周知,数值积分计算并不总能得到精确解,通常只能得到近似解,如何才能得到较高精度的近似解是一个值得研究的问题[8,12],这与积分点的选取密不可分.在实际计算时会发现当积分点数增加时,数值积分结果能收敛到精确解,然而其收敛过程并不是单调的.除此之外,一般情况下,为了克服刚度矩阵的刚化现象会采用较少的单元积分点数计算单元矩阵,避免过多的积分点捕捉刚度矩阵中更多的高次项使其刚性变得更加糟糕.为此,选取恰当的单元积分点数是需要经过数值试验的.本文选取的形函数是Lagrange16点双三次形函数,采用3×3和4×4个Gauss点,4×4个Gauss-Lobatto点在每个单元上进行数值积分试验,确保解的准确性.

4 数值结果

综合以上对耦合方程组(0.1)有限元——有限差分的全离散结果以及数值积分点的选取,运用Matlab编程,模拟在[0,2]×[0,2]区域中,受不同外力后,网格的速度场和应力场的变化.本文参考有限元软件Dyna的后处理模式,用网格的形变表示速度场的变化,给各个小单元标识不同颜色表示应力场的变化.这里为了提高解的精度,更好地体现形变和应力变化,本文设步长h=0.5.图4.1是利用9点Gauss积分得到的三种有限元——有限差分形式的形变图.其中∆t为时间步长,u10、u20为初始速度.9点Gauss积分对应的应力变化图4.2如下.其中色块的颜色越深,表示受到的应力越大;每幅图中的每个小图分别对应各个时间的应力变化.三幅大图分别表示用Lagrange-Euler、Lagrange-Crank-Nicolson和Lagrange-Adams这三种网格剖分方式计算得到的应力图.为了显示每种网格剖分对应的应力变化,下图分别选取两个时间节点t=1,t=2的应力图.

图4.3是利用16点Gauss积分得到的三种有限元——有限差分形式的形变图.如图4.4表示16点Gauss积分对应三种剖分格式的应力变化.为展示每种网格剖分的应力变化情况,本文对各个剖分格式下的计算结果分别选取三个时间点的应力图,从左向右依次对应t=1,t=2,t=3.

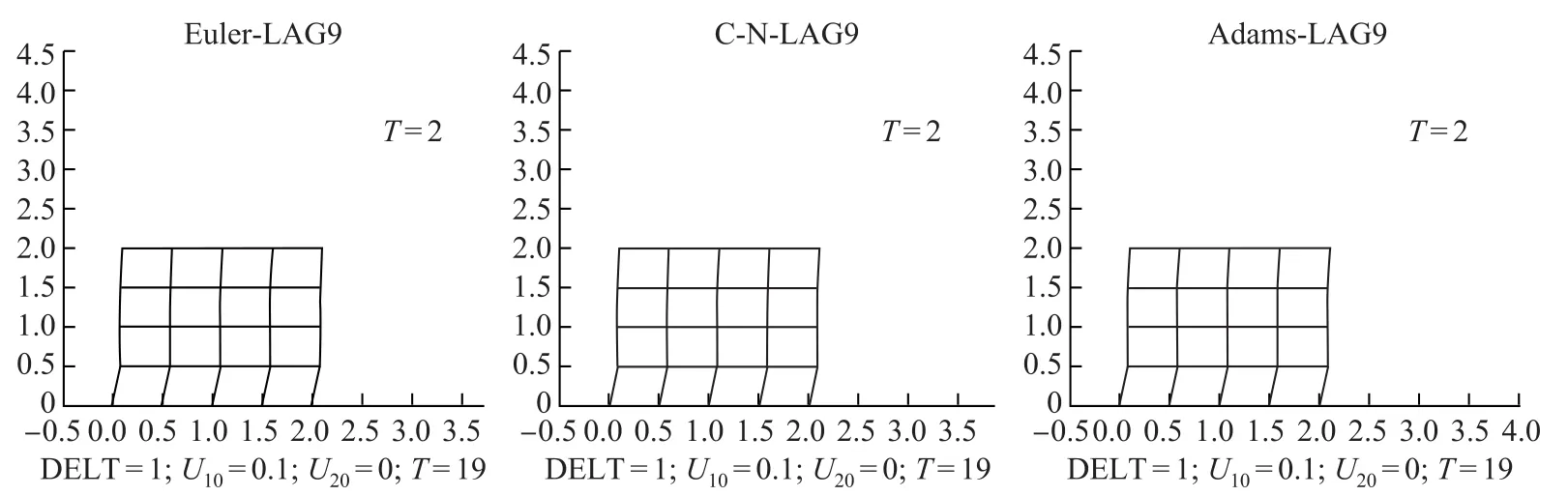
图4 .1 9点Gauss积分,∆t=1,u10=0.1,u20=0Fig.4.1 Gauss integration with 9 points,∆t=1,u10=0.1,u20=0

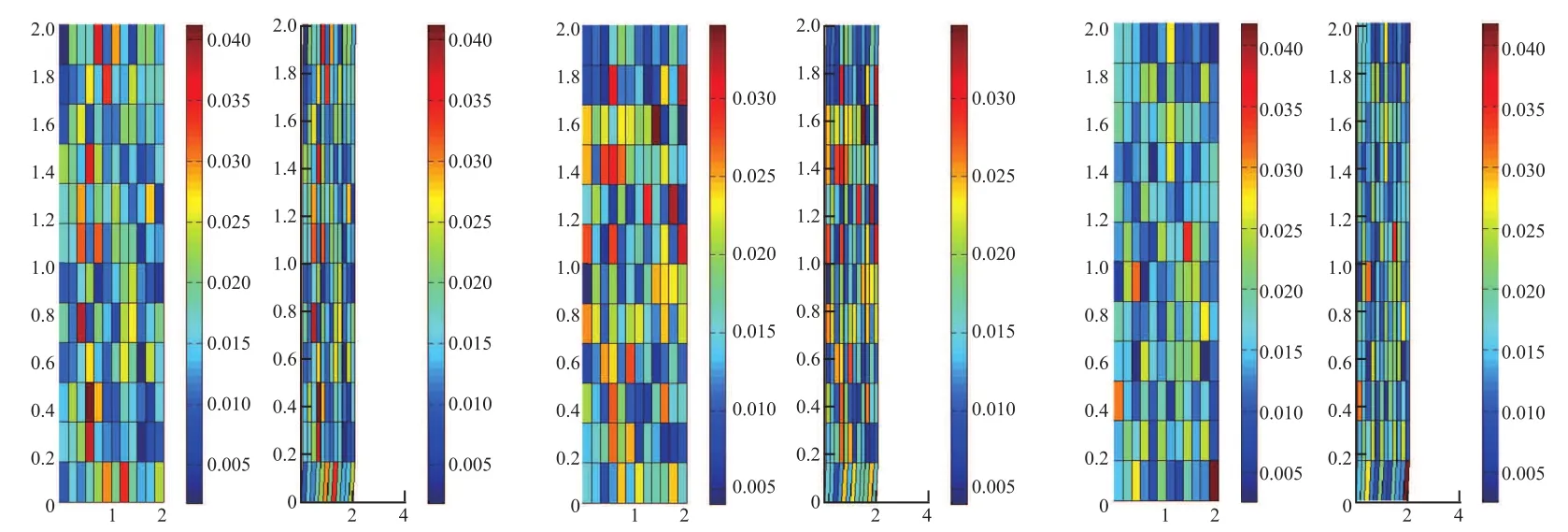
图4 .2 9点Gauss积分对应三种剖分格式的应力变化图Fig.4.2 The stress distribution calculated by Gauss integration with 9 points of three kinds of mesh

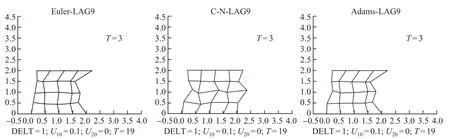
图4.3 16点Gauss积分,∆t=1,u10=0.1,u20=0Fig.4.3 Gauss integration with 16 points,∆t=1,u10=0.1,u20=0

图4 .5是利用16点Gauss-Lobatto积分得到的三种有限元——有限差分形式的形变图.图4.6中三幅图分别表示在Lagrange-Euler、Lagrange-Crank-Nicolson以及Lagrange-Adams剖分格式下,利用16点Gauss-Lobatto积分求得的应力变化图.其中Lagrange-Euler和Lagrange-Adams剖分格式中截取了两个时间点的应力变化图,从左往右分别对应t=1,t=2.Lagrange-Crank-Nicolson格式截取了三个时间点的应力变化图，即t=1,t=2,t=3.

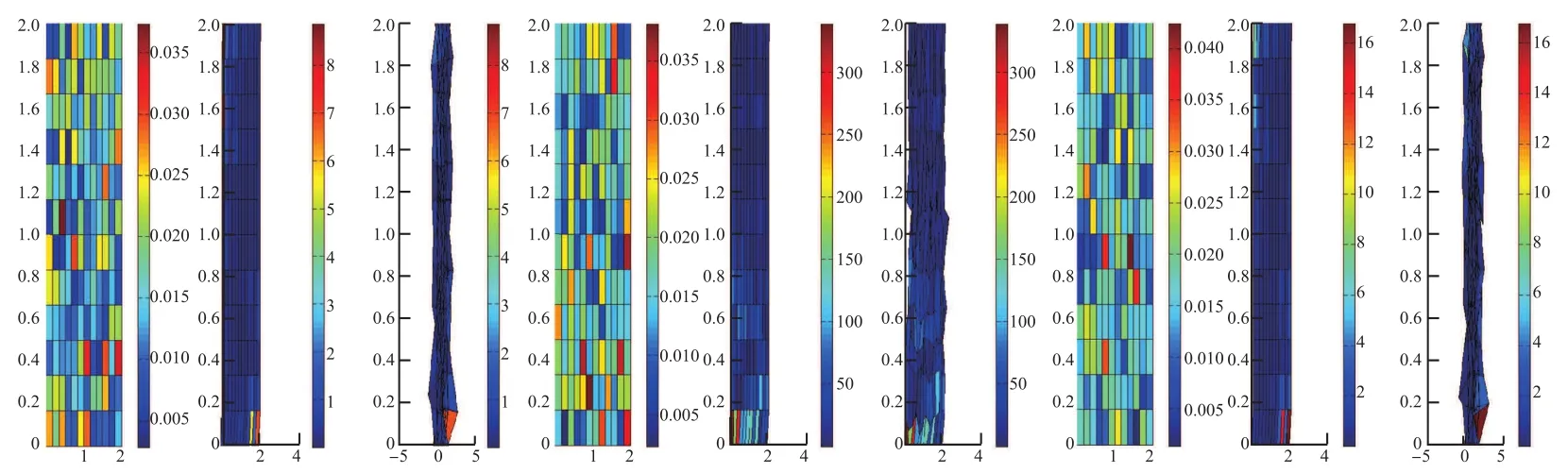
图4 .4 16点Gauss积分对应三种剖分格式的应力变化图Fig.4.4 The stress distribution calculated by Gauss integration with 16 points of three kinds of mesh

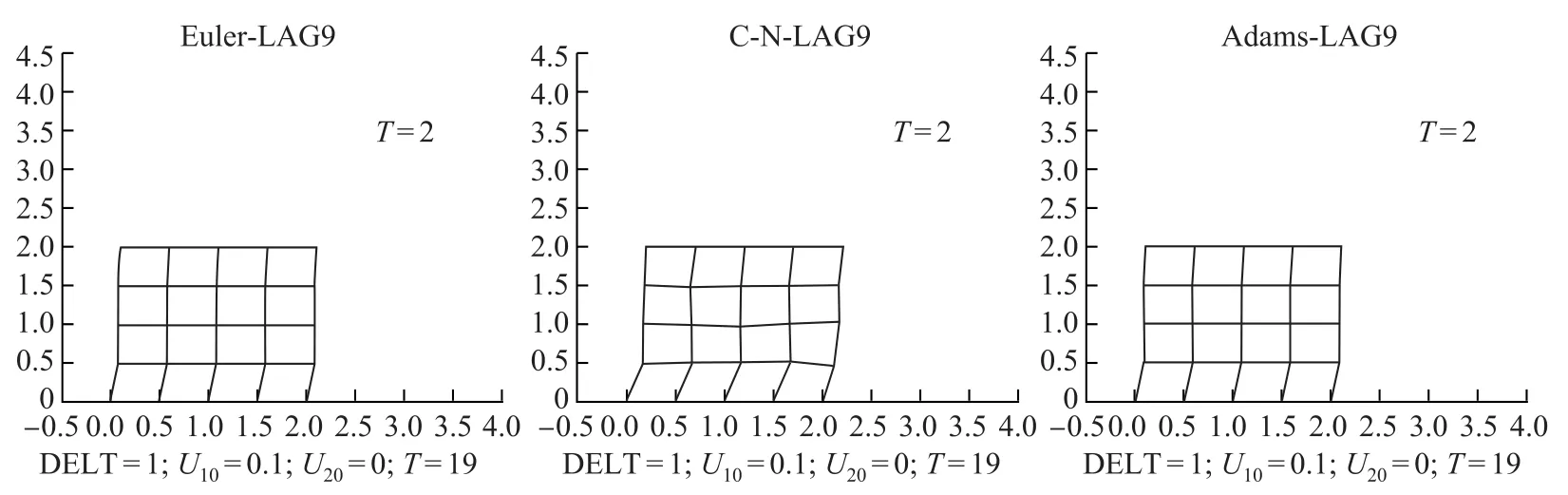
图4 .5 16点Gauss-Lobatto积分,∆t=1,u10=0.1,u20=0Fig.4.5 Gauss-Lobatto integration with 16 points,∆t=1,u10=0.1,u20=0

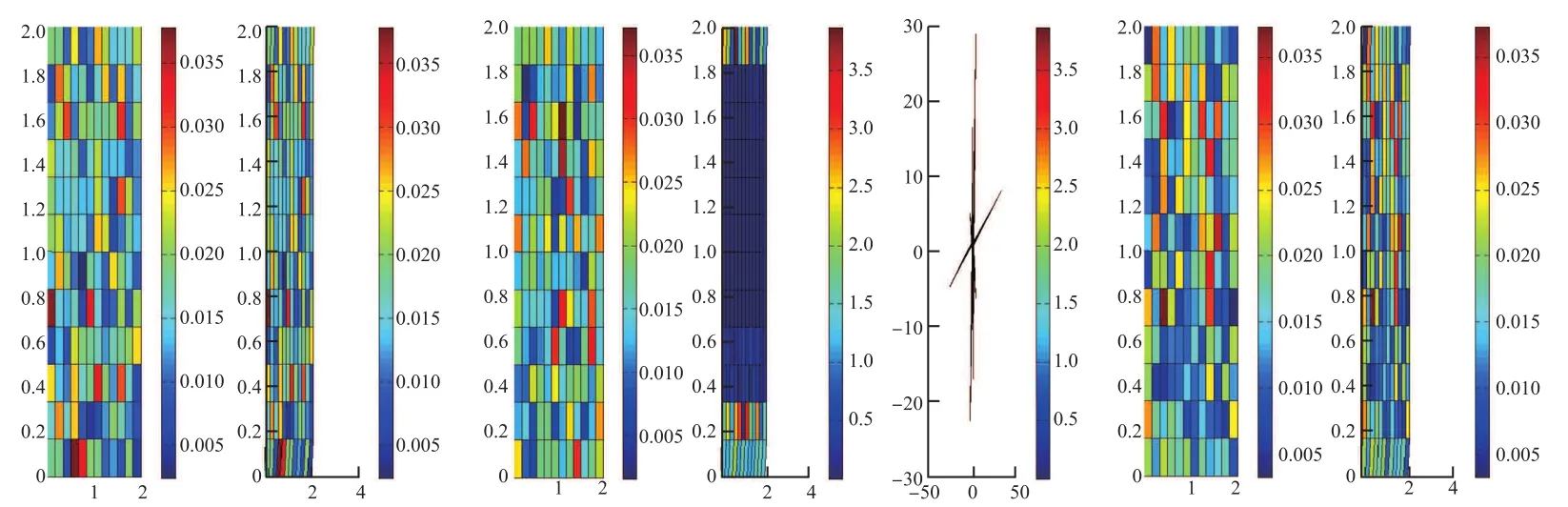
图4 .6 16点Gauss-Lobatto积分对应三种剖分格式的应力变化图Fig.4.6 The stress distribution calculated by Gauss-Lobatto integration with 16 points of three kinds of mesh

5 结论

本文采用有限元方法对空间变量进行离散,主要运用Lagrange16点双三次形函数构造插值函数.再结合三种不同的有限差分对时间变量进行离散,最终求解耦合方程组(0.1)的数值解.文中对刚度矩阵中数值积分的求解,采用不同类型的求积公式进行数值模拟.最终发现,9点的Gauss积分和16点的Gauss-Lobatto积分效果相差不大;16点的Gauss积分更好地体现了形变程度,精确度更高.总体上这三种数值积分方式都可以说明采用Lagrange16点双三次形函数提高了耦合方程组数值解的精度.

6 致谢

作者在写这篇文章时受到各位专家学者的鼓励和指导,特在此对他们的热情帮助和指导表示感谢.

[1]李涵灵.复杂表面接触问题的高性能有限元求解及其数据后处理[D].上海：上海大学,2014.

[2]PHAN-TH IEN N.A nonlinear network viscoelastic model[J].Journal of Rheology,1978,22(3)：259-283.

[3]TANNER R I.Engineering Rheology[M].London：Oxford University Press,2000.

[4]THIEN N P,TANNER R I.A new constitutive equation derived from network theory[J].Journal of Non Newtonian Fluid Mechanics,1977(2)：353-365.

[5]李立康.数值计算方法[M].上海：复旦大学出版社,1999.

[6]LIN Q,ZHOU J.Superconvergence in high order galerkin finite element methods[J].Computer Methods in Applied Mechanics and Engineering,1999,196(3)：3779-3784.

[7]王N成,邵敏.有限单元法基本原理和数值方法[M].北京：清华大学出版社,1997.

[8]HELENBROOK B T.On the existence of explicit hp-finite element methods using Gauss-Lobatto integration on the triangle[J].SIAM Journal on Numerical Analysis,2009,47(2)：1304-1318.

[9]XU Y.On Gauss-Lobatto integration on the triangle[J].SIAM Journal on Numerical Analysis,2011,49(2)：541-548.

[10]李开泰,黄艾香,黄庆怀.有限元方法及其应用[M].北京：科学出版社,2006.

[11]HOU L,NASSEHI V.Evaluation of stress-effective flow in rubber mixing[J].Non linear Analysis Theory Methods and Applications,2001,47(3)：1809-1820.

[12]BOYD J P.A numerical comparison of seven grids for polynomial interpolation on the interval[J].Computers and Mathematics with Applications,1999,38(3)：35-50.

(责任编辑：林磊)

High order interpolation function for surface contact problem

FENG Yun-qing1,HOU Lei1,2
(1.Department of Mathematics,Shanghai University,Shanghai 200444,China; 2.Computational Sciences E-institute of Shanghai Universities,Shanghai 200030,China)

This paper mainly adopts Lagrange bicubic shape function to construct interpolation function and uses finite element method to solve the coup ling equations of surface contact.The Lobatto points are used to construct the interpolation nodes to avoid the Runge phenomenon.Higher shape functions and two different numerical integration methods are adopted to imp rove the accuracy of the numerical solution.According to the above analysis,this article uses Matlab program to simulate the deformation and stress changes in surface contact problem.

finite element;Lagrange;orthogonal integration

O 241

A

10.3969/j.issn.1000-5641.2016.03.002

1000-5641(2016)03-0009-12

2015-05

国家自然科学基金项目(11271247)

冯云青,女,硕士研究生,研究方向为有限元软件应用.E-mail：yqyzsh@126.com.

侯磊,男,教授,博士,研究方向为非线性有限元、自适应方法及应用. E-mail：houlei@shu.edu.cn.