M.MALDONADOJ.PRADAM.J.SENOSIAIN

Department of Mathematics，Salamanca University，Salamanca，Spain

E-mail∶cordero@usal.es；prada@usal.es；idiazabal@usal.es



DIFFERENTIAL OPERATORS OF INFINITE ORDER IN THE SPACE OF RAPIDLY DECREASING SEQUENCES∗

M.MALDONADOJ.PRADA†M.J.SENOSIAIN

Department of Mathematics，Salamanca University，Salamanca，Spain

E-mail∶cordero@usal.es；prada@usal.es；idiazabal@usal.es

We consider the space of rapidly decreasing sequences s and the derivative operator D defined on it.The object of this article is to study the equivalence of a differential operator of infinite order；that isconstant numbers an a power of D. Dn，meaning，is there a isomorphism X（from s onto s）such that Xϕ（D）=DnX？.We prove that if ϕ（D）is equivalent to Dn，then ϕ（D）is of finite order，in fact a polynomial of degree n.The question of the equivalence of two differential operators of finite order in the space s is addressed too and solved completely when n=1.

Ordinary differential operators；sequence spaces；operators on function spaces 2010 MR Subject Classification47E05；46A45

1　Introduction

The problem of the equivalence of differential operators was treated by many authors in different contexts.The works of Delsarte and Lions［1-5］are well-known where they introduced the notion of“operateur de transmutation”.Later on，in the 1960s，the term“equivalence of operators”appeared，being the subject intensively studied［6-23］.

Let us recall the concept of“operateur de transmutation”.If T and S are two diferential operators in a space H，an operator X is an“operateur de transmutation”from T to S when X is an isomorphism from H onto H such that SX=XT.

The operators T and S are said to be equivalent when there is an“operateur de transmutation”from T to S；that is，there an isomorphism X such that SX=XT.

If T and S are differential operators and H a space of real variable functions，the problem is solved only in particular cases and it seems that it is difficult to give a general solution as Delsarte and Lions pointed out as far back as 1957.On the contrary，the situation when T and S are differential operators in the complex plane and H is a space of functions of a complex variable is very different；in fact，when H is the space of entire functions of a complex variable and T and S are differential operators of the same order with constant coefficients，then T and Sare equivalent.Several authors treated the question in spaces of analytic functions considering differential operators with or without singularities as well as differential operators of infinite order.

Nagnibida N.I.and Oliinyk N.P［21］studied the equivalence of a differential operator of infinite order to a power Dnof the usual derivative in analytic spaces.They proved that the only differential operators of infinite order equivalent to Dnare differential operators of finite order；that is（in the space of analytic functions on a finite disc）and6=0（in the space of analytic functions on the whole complex plane）.

As the spaces of analytic complex functions can be considered as sequence spaces，it seems natural to study the equivalence of differential operators on sequence spaces.As the results depend greatly，not only on the differentials operators，but on the sequence spaces taken，we think it convenient to work with a concrete sequence space.A sequence space that plays an important role in mathematics is the space of rapidly decreasing sequences s.It is enough to observe that very well known space functions as=｛2π-periodic，funcions on R｝，S（R）（the Schwartz space）C，f infinitely differentiable｝are isomorphic to s［24］.Using this fact，it is easy to see that two differential operators of order one with constant coefficients are not equivalent on the space

In this article，we consider a continuous differentiable operator of infinite order ϕ（D）with constant coefficients in the sequence space s and prove that，as in the case of analytic functions，its equivalence to a power of the usual derivative Dnimplies that it is of finite order，in fact，a polynomial of degree nWe consider，too，the problem of the equivalence of two differential operators of finite order in the space s not having，for n＞1，a close result. For n=1，a differential operator of order one is equivalent to D if and only if|ϕ1|=1.

2　Terminology

An infinite power series space Λ∝（α）（respectively a finite power series space Λ1（α））is the sequence space

where（αn）is an increasing sequence of positive real numbers going to infinity.They are Fr´echet spaces with a canonical basis（en），the topology given by the norms

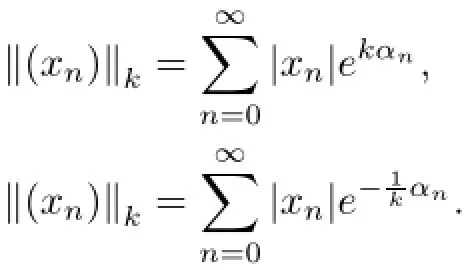
If αn=n，Λ∝（α），（Λ1（α））represent the spaces of complex analytical functions in C（in a disc D（0，R）（0＜R＜∞））.

An important infinite power series space（αn=logn）is the space s of rapidly decreasing sequences

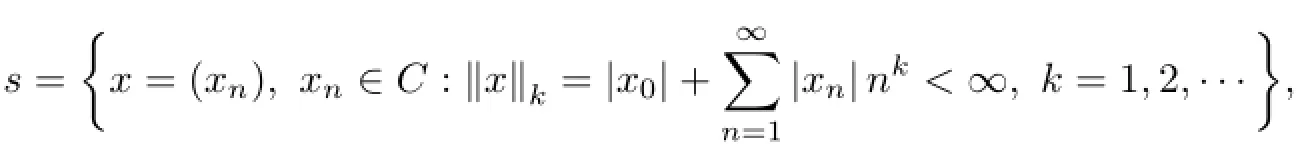
which is a nuclear space［24］.

A linear operator T from s to s is continuous if and only if

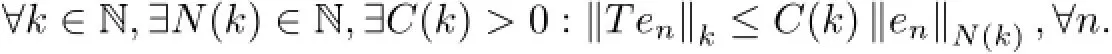
The usual derivative D from s to s，defined by Den=nen−1，en=δjn，is a linear continuous operator on s.

A linear operator S is a finite differential operator of order n ifk=0，1，2，···，n.A linear operator，is a differential operator of infinite order and will be denoted by ϕ（D）in the sequel and is assumed to be continuous.ϕ（D）is equivalent to Dnin the sequence space s if and only if there is an isomorphism T such that ϕ（D）T=TDn.

3　Statement of Problem

Given the infinite differential operator，we study the equivalence of this operator to the operator Dnin the sequence space s.

The main result of this article is

The following propositions are used in the proof of the theorem.

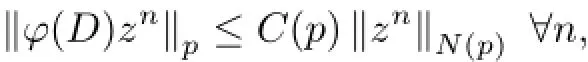
which implies

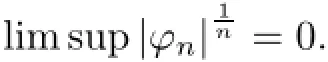
Secondly，the order of ϕ（z）is at most 1.Let us compute

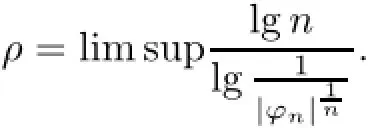
As

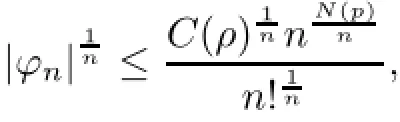
it follows that ρ≤1.

Finally，ϕ（D）=pn（D）eaD.ϕ（D）has n linearly independent zeros because of the equivalence to Dn.As

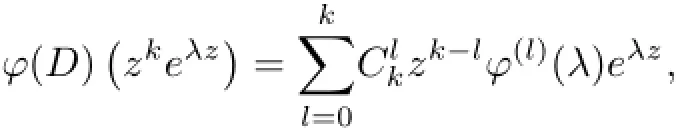
if λ0is a zero of ϕ（λ）with multiplicity ν，then eλ0z，zeλ0z，···，zν−1eλ0zare zeros of ϕ（D），which implies that ϕ（λ）has，at most，n zeros taking account of multiplicities［21］.

Therefore，by［25］，

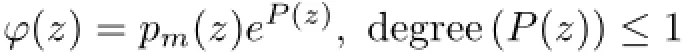
and so

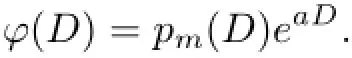
As the operator pm（D）eaDhas m solutions on s（the operator eaDis injective），then m=n.

Proposition 3.3ϕ（D）=pn（D）eaDimplies that Teλzis given by

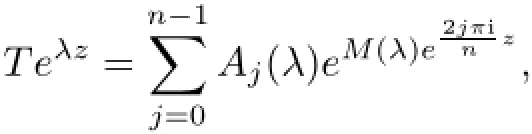
where

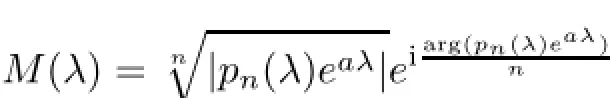
with arg（pn（λ）eaλ）∈［0，2π）.

ProofIt is enough to solve the equation

Proposition 3.4The r-norm of the elements eλzin s is given by

where Pris a polynomial of degree r and its coefficients are natural numbers.

ProofCompute the sum

Proposition 3.5The r-norm of the elements Teλzin s is given by

where for a fixed q，0＜q≤n−1，

the Dm，2≤m≤r−1 are natural numbers and the with h=1，2，···，r， s=0，1，···，n−1 solutions of a system

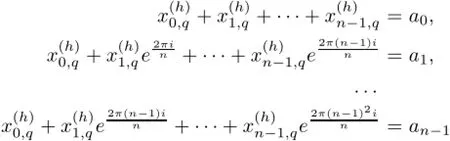
with（a0，a1，···，an−1）all zero but one（depending on q and r）.

ProofRecall that Teλzis given by the formula in Proposition 3.3.

As kr=k（k−1）···（k−r+1）+Dr−1k（k−1）···（k−r+2）+···+D2k（k−1）+k，where Dm∈N with 2≤m≤r−1，Dr=D1=1，it follows that

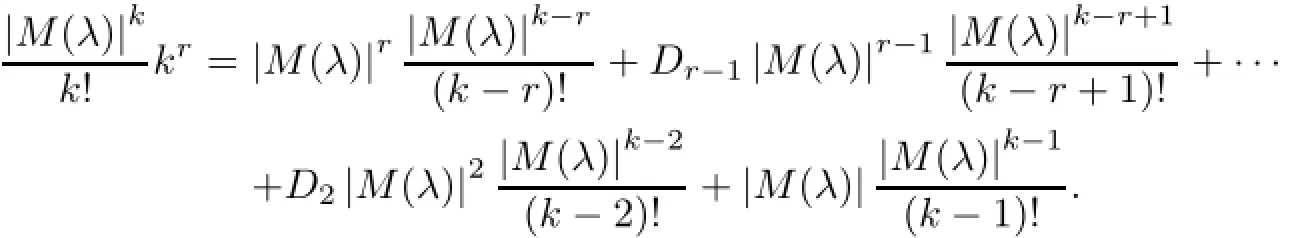
Therefore，for a fixed q，

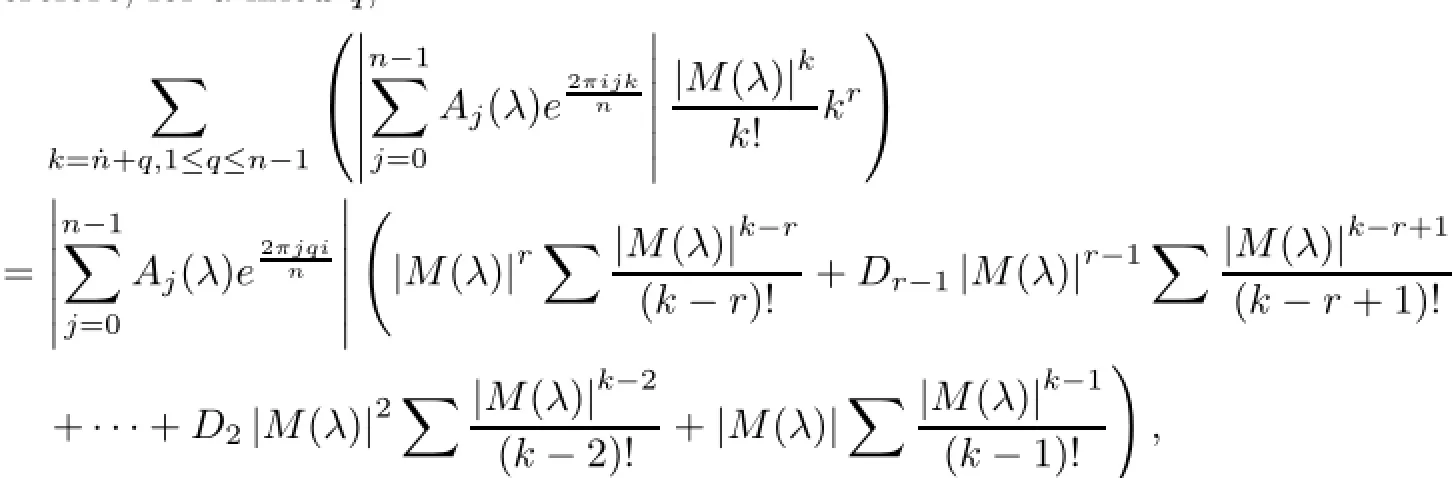
where all sums are on k=˙n+q，1≤q≤n−1.For q=0，we consider the expression

and proceed in a similar way.

Finally，observe that all sums that appear in the previous formulas can be written as，whereare as indicated above.Consider，for instance，the sum

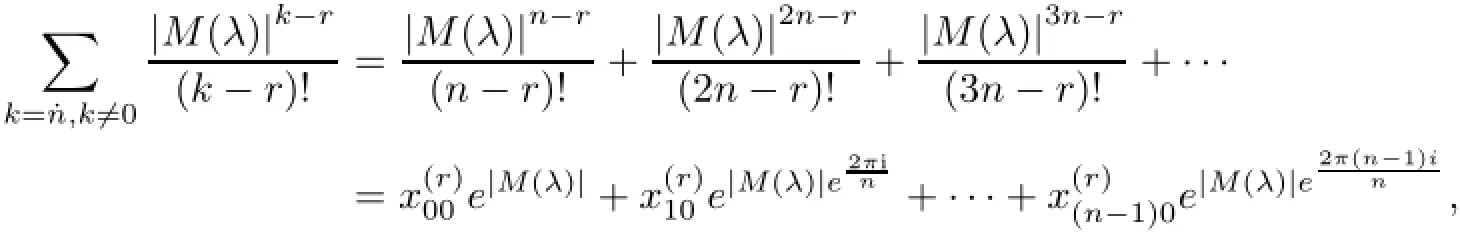
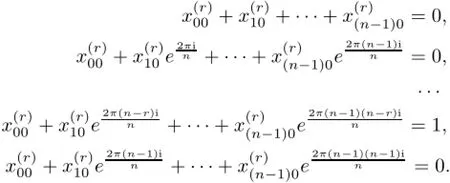
Note also that the numbers x（r）sqare，in general，complex numbers but the sumsare real and positive.

Proof of TheoremAs ϕ（D）is equivalent to Dn，we have ϕ（D）=pn（D）eaD.Let us prove a=0.

The isomorphism T verifies the condition：

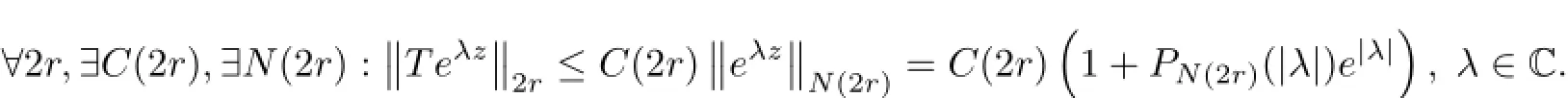
Therefore，all sums that appear in formula 2 are for instance less than or equal to

Consider，for instance，the following one，

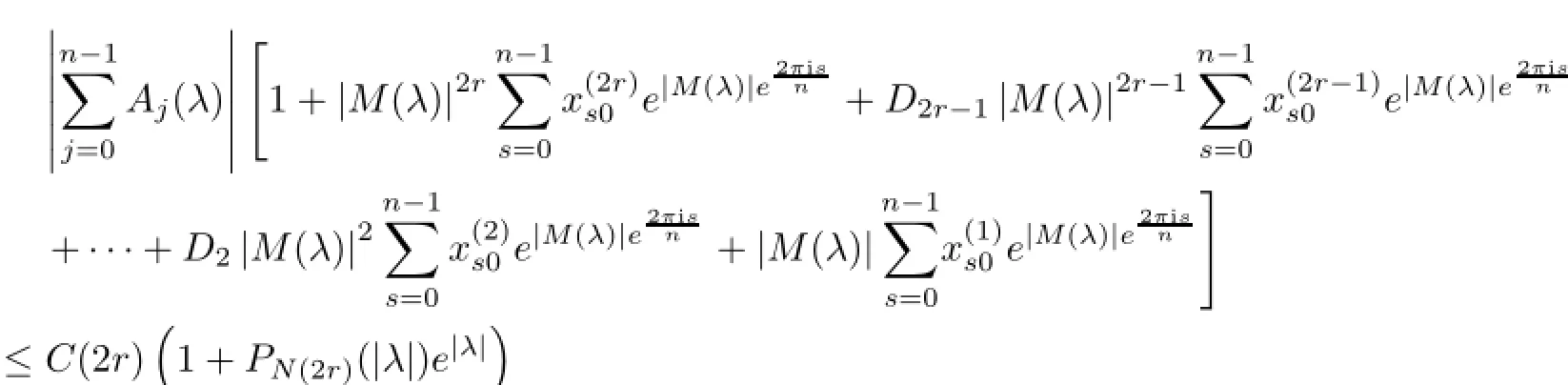
and write

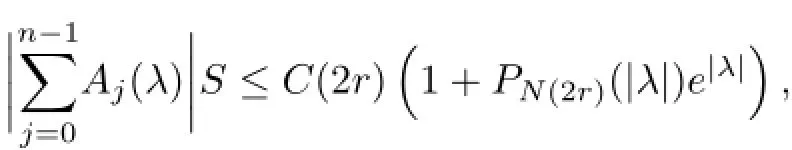
where

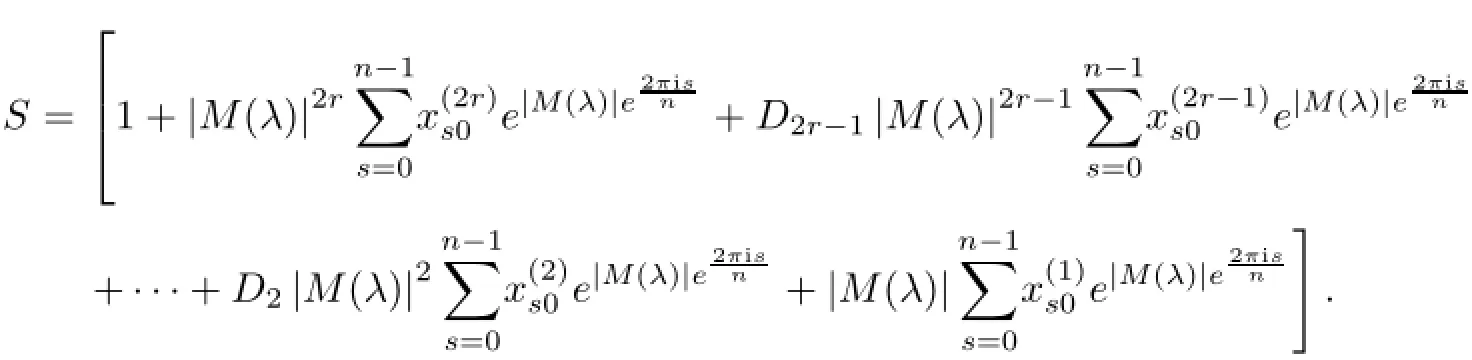
Writting

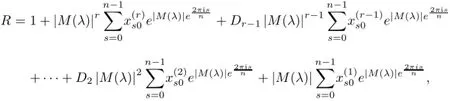
we have

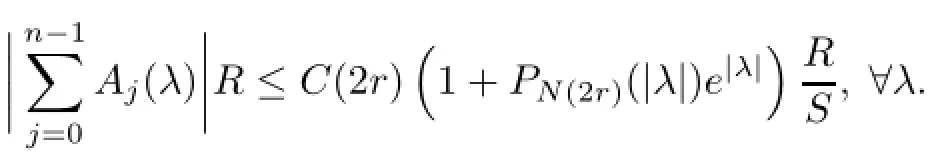
4　Equivalence of Finite Differential Operators on s

In this section，we address the question of the equivalence of a finite differential operator of order n to Dn；that is，are all operators of the formequivalent to Dn？

Proposition 4.1The operator pI+qD（p，q 6=0）is equivalent to D if and only if|q|=1.

ProofFor this proposition，two facts（proved below）are used.

a）pI+D is equivalent to D for p 6=0，which implies thatis equivalent to qD.

b）qD is equivalent to D if and only if|q|=1. Then：

1）Assume that pI+qD is equivalent to D.As pI+qD is equivalent to qD，it follows that qD is equivalent to D and so|q|=1.

2）If|q|=1，then qD is equivalent to D.As pI+qD is equivalent to qD，the result follows.

Proposition 4.2pI+D is equivalent to D.

ProofConsider the operator T given by Tzn=znepzand T−1zn=zne−pz.It is easy to check that T is an isomorphism such thatis equivalent to

Proposition 4.3The operators qDnand Dnare equivalent if and only if|q|=1.

ProofAssume that qDnand Dnare equivalent.Then，there is an isomorphism T such that T（qDn）=DnT；therefore，，0≤s≤n−1.Suppose without lost of generality that，（all，0≤s≤n−1，cannot be zero），then

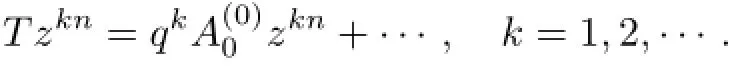
The continuity condition of T implies that|q|≤1.Proceeding in the same way with T−1，it follows that|q|≥1.Conversely，if|q|=1，it is seen that the operator T，given by the following equations

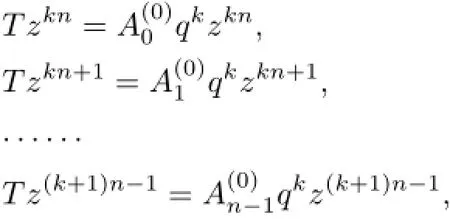
is an isomorphism that solves the equation T（qDn）=DnT.

Remark 4.4I+D and D are equivalent and so are（I+D）nand Dn.The operators eaDare not continuous for any a∈C and，therefore，eaDis not equivalent to D.We believe thatis equivalent to Dnif and only if|pn|=1，which is true if n=1，and is equivalent to the operator D in the space s if and only if ϕ（D）=ϕ0I+ϕ1D and|ϕ1|=1.

References

［1］Delsarte J.Sur certaines transformations fonctionnelles relatives aux equations lineaires aux derivees partielles du second ordre.C R Acad Sci Paris，1938，206

［2］Delsarte J，Lions J L.Transmutations d’op´erateurs diff´erentiels dans le domaine complex.Comment Math Helv，1957，32：113-128

［3］Lions J L.Op´erateurs de Delsarte and probl´emes mixtes.Bull Soc Math France，1956，84：9-95

［4］Lions J L.Quelques applications d op´erateurs de transmutation.La th´eorie des´equations aux d´e riv´ees partielles.Nancy，1956，Colloques Internationaux du Centre National de la Recherche Scientifique，Centre National de la Recherche Scientifique，Paris，1956，71：125-137

［5］Lions J L.Solutions´el´ementaires de certains op´erateurs diff´erentielles´a coefficients variables.J Math Pures Appl，1957，36（9）：57-64

［6］Chiardola A M，Guala E.Risultati di sintesi spettrale per una classe di operatori equivalenti alla derivata. Boll Un Mat Ital，1975，11：456-472

［7］Chuan Wai-fond.The unitary equivalence of compact operators.Glasgow Math J，1985，26（2）：145-149

［8］Cramer G L.Equivalence of differential and perturbed differential operators in spaces of analytic functions of several variables in polycircular domains.Mat Zametki，1967，1：565-574

［9］Fage M K.Operator-analytical functions of one independent variable.Dokl Akad Nauk SSSR，1957，112：1008-1011（in Russian）

［10］Fage M K.On the equivalence of two linear differential operators with analytic coefficients.Studies on contemporary problems in the theory of functions of a complex variable.Moscow：Fizmatgiz，1961：468-476

［11］Fi˘sman K M.On the equivalence of differential operators in the space of functions analytic on a disc.Uspehi Mat Nauk，1964，19：143-147（in Russian）

［12］Fi˘sman K M.Equivalence of certain linear operators in an analytic space.Mat Sb，1965，68（110）：63-74（in Russian）

［13］Fi˘sman K M.The reduction to diagonal form of certain classes of row-finite matrices in analytic spaces on the disc.Teor Funkci˘i Funkcional.Anal i Prilo˘zen，1968，7：27-36（in Russian）

［14］Fi˘sman K M.The similarity of certain classes of row-finite matrices in analytic spaces on the disc.Teor Funkci˘i Funkcional.Anal i Prilo˘zen，1971，13：112-140（in Russian）

［15］Fi˘sman K M.The equivalence of differential operators with a resular singular point.Funct Anal Appl，1974，8：169-171

［16］Gaborak Y N，Kushnirchuk I F，Ponmyuk M I.Equivalence of third-order differential operators with a regular singular point.Siberian Math J，1978，19：882-886

［17］Guala E.Su una classe di operatori non lineari equivalenti all derivata nello spazio delle funzioni analitiche su C.Boll Un Mat Ital，1978，15（A）：601-609

［18］Kushnirchuk I F，Nagnibida N I，Fi˘sman K M.Equivalence of differential operators with a regular singular point.Funct Anal Appl，1974，8：168-171

［19］Maldonado M，Prada J，Senosiain M J.On differential operators on sequence spaces.J Nonlinear Math Phys，2008，15（3）：45-352

［20］Maldonado M，Prada J，Senosiain M J.On differential operators of infinite order in sequence spaces.Cyprus：Proc Sixth Workshop“Group Analysis of Differential Equations&Integrable Systems”，2012

［21］Nagnibida N I，Oliinyk N P.On the equivalence of differential operators of infinite order in analytic spaces. Math Notes，1977，21：19-21

［22］Tam P K.On the unitary equivalence of certain classes of non-normal operators.Can J Math，1971，23（5）：849-856

［23］Viner I J.Transformation of differential operators in the space of holomorphic functions.Uspehi Mat Nauk，1965，20：185-188

［24］Meise R，Vogt D.Introduction to functional analysis.New York：The Clarendon Press，Oxford University Press，1997

［25］Markushevich A.Theory of functions of a complex variable.NY：Chelsea Publishing Company，1977

February 18，2014；revised May 07，2015.The authors are supported by MIMECO under project MTM2012-38445.

†Corresponding author