☉华中师范大学数学与统计学院 张依淼 童扬平 徐章韬

韦达定理课程改革的理据*

☉华中师范大学数学与统计学院 张依淼 童扬平 徐章韬

一、引言

韦达定理是一元二次方程中根与系数关系的精髓，有着丰富的历史内涵和美学价值，其完美的对称性也是群论中轮换对称的基础.从韦达定理的应用来看，韦达定理在直线与圆锥曲线位置关系的讨论中应用广泛；从课程拓展来看，以韦达定理为基础的多项式在数据结构和计算机算法，计量经济学、运筹学等方面都有间接涉及；从理论价值来看，韦达定理可推广至一元n次方程中根与系数的关系，技巧精湛，理论严密.但是，在2000年出台的《初中数学课程标准（实验稿）》中删去对韦达定理的要求；2011年出台的新课程标准［1］增加了“了解一元二次方程根与系数关系”的要求，但只是作为选学的内容，没有给予韦达定理足够的重视.本文将从韦达定理的历史内涵、美学特征及数学方法比较等角度来寻找韦达定理在初中数学教材中应该受到重视的依据.

二、韦达定理的历史［2］

任何一个数学定理的发现、论证及最终形式都是众多数学家前仆后继的结果.韦达定理的创立必然也经历了这样一个过程.在数学发展的历史长河中，方程的求解始终是一篇好文章，而方程中根与系数一开始并没有引起人们的注意.15世纪意大利数学家在他书中，用配方法解出了二次方程，但是并未提及根与系数之间的关系.可以说，那时根与系数真是一个盲点.直到1545年，卡丹给出了三次方程的求根公式.从此，开始了根与系数关系的探索之旅.卡丹在其书中表示，三次方程中，正根之和与负根之和的差等于二次项系数.后来数学家邦贝利也论证了这一观点.

1615年韦达在《论方程的整理与修改》一书中给出了方程根与系数关系.他是第一个清楚地认识到根与系数关系的人.在根的范围内，对一元二次方程、三次方程分别给出了如下结论：（1）（a+b）x-x2=ab，则x=a或x=b.（2）x3+b=ax（a>0，b>0），则有在四次和五次方程中，韦达也给出了类似的结果.但是需要注意的是，伟大的结论仅在正根的范围内，因为排斥了负根，故其结论并不完整，但其为根与系数的研究跨出了重要的一大步，也为后人的研究铺平道路.

吉拉尔则在韦达定理的基础上给出了一般表达式，也就是我们通常所说的代数基本定理：xn+a2xn-2+a4xn-4+…=a1xn-1+a3xn-3+a5xn-5+…，随即我们得到了其根与系数的一般表达式：x1+x2+…+xn=a1（一次和），x1x2+x2x3+…+xn-1xn=a2（二次和），x1x2x3+x2x3x4+…+xn-2xn-1xn=a3（三次和），…，x1x2x3…xn=an（n次和）.吉拉尔的代数基本定理是对韦达定理的补充，而他的另一个重要贡献是提出了方程根的“幂和公式”.

此后相隔一个世纪，牛顿得到了与吉拉尔一样的结论：xn-pxn-1+qxn-2-rxn-3+sxn-4-txn-5+uxn-6+…=0.

设p=a，pa+2q=b，pb+qa+3r=c，pc+qb+ra+4s=d，pd+ qc+rb+sa+5t=e，pe+qd+rc+sb+ta+6v=f.后人把上述结论称之为“牛顿幂和公式”.此后方程根与系数的关系就是非常容易理解的了.

牛顿幂和公式引发了对对称函数的普遍关注，对称函数是代数组合学中一个重要的研究领域，研究要点集中于对称群及对称多项式的代数组合性质.在数学的其他领域都有广阔的应用.范德蒙指出：“根的任何有理对称函数都可以用方程的系数表示出来.”随后构造出了范德蒙行列式.n阶范德蒙行列式是对称函数的演变，将行列互换结果仍然不变，具有完美的对称性.

此后许多数学家在对称函数中前仆后继取得了重要研究成果.其中拉格朗日在表示对称函数时采用了欧拉引入的求和符号∑，而拉格朗日函数的对称性先后衍生出了对偶问题，对偶问题的对称性在线性规划，以及在最优化处理中起到了前所未有的积极作用.

三、韦达定理的对称美

韦达定理体现了对称之美.在韦达定理所阐述的根与系数的关系中，两根之间存在对应关系.由多项式的对称变换，我们自然可以得到根与系数的对称性，群论中的对称性也正好反映了多项式中的对称性.

将多项式x1+x2中的x1与x2进行调换，即可得到x2+x1.

x1+x2中的对称变换有两个，即：

实际上，一元二次方程ax2+bx+c=0的图像是与x、y轴有交点的抛物线，初中直接给出对称轴公式，到上高中后，一元二次方程在函数图像中频繁使用，再后来学习导数后，明白对称轴对应值是一元二次方程导函数为零时所得值，无论图像开口向上或向下，都可以根据图形找出其完美的对称性.所以韦达定理的对称性同样适用于一元三次方程、一元四次方程，这其中需要借助于导函数为零求出对称轴，进而找到其对称中心.

设f（x）=x3+a1x2+a2x+a3，则f′（x）=3x2+2a1x+a2，f″（x）= 6x+2a1.令f″（x）=0，可得其对称轴为所以f（x）关于点中心对称.同理在一元四次函数中f（x）的对称轴为，其对称中心亦为

当我们把韦达定理推广到一元n次多项式函数中的根与系数关系，可设xi（i=1，2，3，…，n）是方程xn+a1xn-1+a2xn-2+…+an-1x+an=0的n个根，则有结论：

由一元二次函数的对称性自然也能推得一元n次多项式函数方程的对称性，其图形对称应以对称轴为中心展开.

由此可见韦达定理中根与系数关系的对称结构具有简单和谐的内涵，是数学和谐美的一个典范.韦达定理的对称式x+y和xy具有简单和谐的对称内涵，常见的x2+y2=（x+y）2-2xy就是把复杂的多项式，用韦达定理的对称式加以表达，于是构成了一道别样风景.韦达定理的对称性还体现在对称轴上，从一元二次方程的图像中，我们通过找到对称轴.再到一元n次多项式中，通过求导可以找到对称轴，构成图形对称，这都要归功于韦达定理中根与系数关系，它是沟通对称性、对偶性、奇偶性的枢纽，其对称轴也架起了原函数、导函数之间的桥梁.真有“天堑变通途”之畅意.

四、韦达定理中的思想方法

1.设而不求

例1已知椭圆C的中心在坐标原点，焦点在x轴上，椭圆C上的点到焦点距离的最大值为3，最小值为1.若直线l：y=kx+m与椭圆C相交于A、B两点（A、B不是左右顶点），且以AB为直径的圆过椭圆C的右顶点，求证：直线l过定点，并求出该顶点的坐标.［3］

设A（x1，y1），B（x2，y2），联立方程得（3+ 4k2）x2+8mkx+4（m2-3）=0，所以Δ=64m2k2-16（3+4k2）（m2-3）>0，3+4k2-m2>0.

所以y1·y2=（kx1+m）·（kx2+m）=k2x1x2+mk（x1+x2）+m2=

又因为以AB为直径的圆过椭圆的右顶点D（2，0），

所以kAD·kBD=-1，所以，即y1y2+x1x2-2（x1+x2）+4=0.

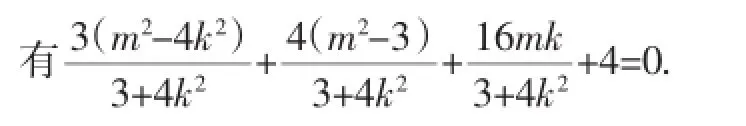
使用韦达定理解题时，不求根但用根，减少了计算量并且结构更加清晰.其实，通过观察求解的过程可以知道，在联立方程组消除y之后，交点坐标就成了一个一元二次方程的解.而后面的关系式中除常数项外就只有y1y2，x1x2，x1+x2，这些项都可以利用韦达定理表示出来，所以不需要求根，由椭圆方程中的求解思想可以推出一般的圆锥曲线的方程，也可以利用韦达定理中“设而不求”的思想.

2.沟通已知与未知的联系

韦达定理形式简单却蕴含着丰富的数学知识内容.在中考数学题目中，我们见到不少有运用韦达定理根与系数关系，求方程中参数的值，求代数式的值，结合判别式讨论根的符号特征，以及由韦达定理的逆定理，构造一元二次方程辅助解题等.这些内容会直接或间接展示根与系数之间的关系，虽然课程中未作必修，但题目中涉及的，教师也会要求学生自觉掌握.在每一年高考试卷中，以直线与椭圆、双曲线及抛物线等的位置关系为背景，涉及弦长计算、中点坐标知识、参数取值、定值计算、定点确定、面积计算、最值探求、存在性判断等众多问题中，利用韦达定理“设而不求”，整体换元，大大地简化计算.所以，提高韦达定理在初中教材中的地位，要求学生掌握韦达定理，提高学生灵活解决问题的能力，为高中阶段解决圆锥曲线的问题打下良好的基础.

五、小结与思考

通过以上分析可知，韦达定理的历史内涵对后续数学知识的学习具有重要意义.韦达定理在对称群、对称函数、导函数、行列式、一元n次多项式等知识点方面起到了积极作用.不管是对于二次还是更高次方程，韦达定理的表达式都表现出完美的对称性，这正是群论的基础，因此学生对于韦达定理的熟练掌握必然能够帮助学生学习更高观点的数学知识.韦达定理的学习有利于学生后续数学知识的发展，这符合新课程改革提出可持续发展的要求.

课程内容的改革对于每一个内容的增减，不仅要考虑知识的难易程度，重要的是要考虑知识点在整个学科中的地位，及其对于学生发展的影响.基于以上的分析，我们有足够的理由认为，现阶段教材对于韦达定理的重视程度不够.不仅不能够删除韦达定理的内容，也不应该将之作为选读的内容，应该作为必修内容，让学生理解掌握并能够灵活应用.课程内容改革关系到学生未来知识的发展走向，我们需审时度势.

1.中华人民共和国教育部.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2.张小明，汪晓勤.根与系数关系简史［J］.中学教研（数学），2004（8）.

3.熊惠民.数学思想方法通论［M］.北京：科学出版社，2010.H

*项目：华中师范大学研究生教学改革项目“数学教育方向研究生学术能力提升的研究”的部分成果.