孙东阳， 陈国平， 张保强

(1.重庆大学航空航天学院 重庆，400044) (2.南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016) (3.厦门大学航空航天学院 厦门，361005)



随机和认知不确定性量化的置信区域法*

孙东阳1， 陈国平2， 张保强3

(1.重庆大学航空航天学院 重庆，400044) (2.南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016) (3.厦门大学航空航天学院 厦门，361005)

针对非线性机械系统中混合不确定性量化的问题，提出了随机和认知不确定性量化的置信区域法。首先，分别用概率论方法和区间方法来处理混合不确定性中的随机不确定性和认知不确定性，得到混合不确定性的置信区域；然后，为了在时间域内对不确定性进行传播，对传统双层循环蒙特卡罗抽样方法进行了改进；最后，以非线性质量-弹簧-阻尼系统为例讨论了基于混合不确定性分析方法的有效性。结果表明，同时考虑随机不确定性和认知不确定性，有利于提高系统设计的可靠性，为非线性机械系统的设计与精度分析提供了理论依据。

置信区域; 随机不确定性; 认知不确定性; 蒙特卡罗

引 言

在非线性机械系统的分析中，不确定性的处理作为一个研究热点，已经受到越来越广泛的关注[1-5]。

不确定性按照其数据信息的掌握情况通常分为随机不确定性和认知不确定性[6-7]。随机不确定性[8-9]源于系统行为的固有随机性，是一种不可避免的不确定性。认知不确定性[10]是由于缺乏数据引起的，是可以随着认识的深入而减少的不确定性。在处理随机不确定性时，通常选用传统概率论方法[11]。然而，在处理认知不确定性时，数学结构的选择一直是一个挑战性问题[12]。模糊集理论[13]、区间分析[14-15]、证据理论[16]和可能性理论[17]已经广泛地应用于研究认知不确定性。当系统中同时存在随机和认知不确定性时，处理这样的问题将面临两方面的挑战。首先，是选择合适的数学结构去描述这两种不确定性；其次，需要将两种不确定性进行分离，以分析各种不确定性对结果的贡献程度[18]。目前，处理这类混合不确定性的方法主要分为概率边界方法，二阶概率论方法和Demspster-Shafer证据理论[19]。这3类混合不确定性分析方法在分析系统的时域响应时都只能分析响应的极值或特定时刻的系统响应[20]。笔者提出了随机和认知不确定性量化的置信区域法，该方法能够在时域内对系统响应进行分析;随后，提出了改进的双层循环蒙特卡罗抽样方法; 最后，以非线性质量-弹簧-阻尼系统为研究对象，用随机和认知不确定性量化的置信区域法对模型参数中存在的不确定性进行了分析。

1 非线性质量-弹簧-阻尼系统动力学建模

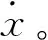
(1)

其中：m为质量;c为阻尼;k和kf分别为线性刚度和非线性刚度。

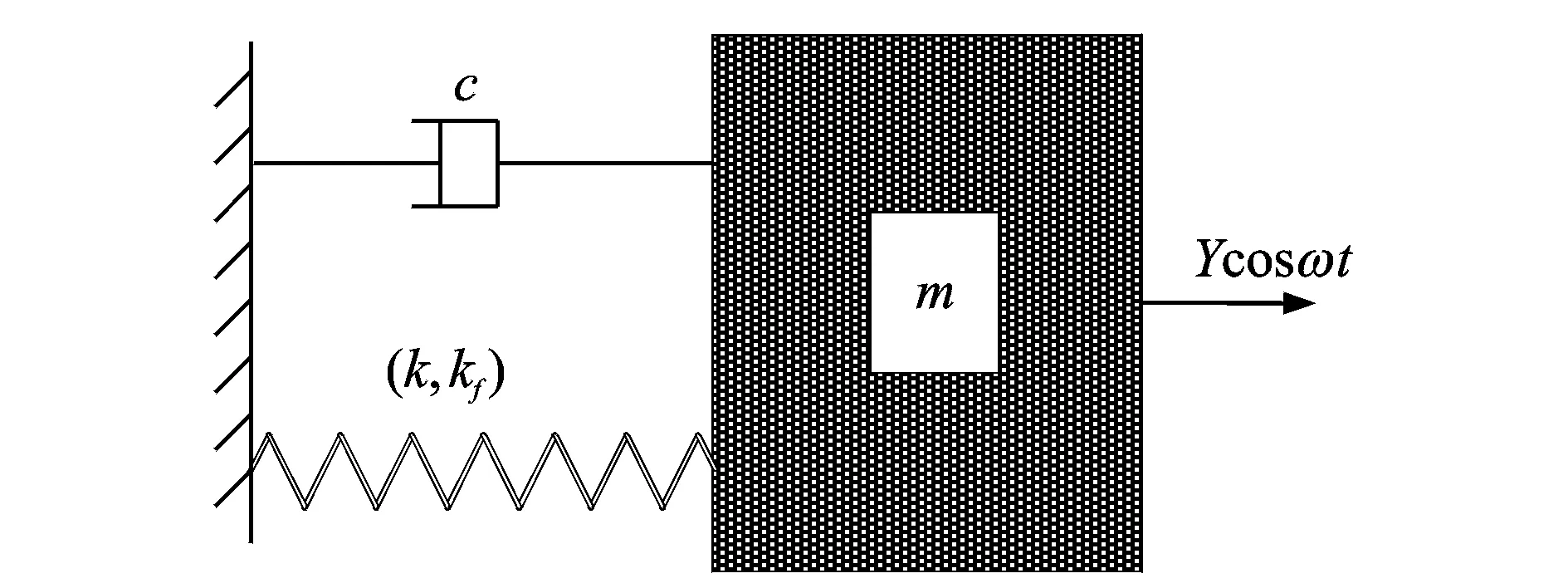
图1 非线性质量-弹簧-阻尼系统Fig.1 Nonlinear mass-spring-damper system

(2)

限定系统的非线性及阻尼比较弱

0≤ε≪1,ζω0=εμ>0,μ=O(1)

该系统不具有精确解，可采用多尺度法研究解的一次近似。设

x(t)=x0(T0,T1)+εx1(T0,T1)

(3)

将式(3)代入式(2)，比较ε的同次幂得线性偏微分方程

通过对该方程组进行求解可以得到Duffing系统的一次近似解。研究发现，该Duffing系统在简谐激励下有可能出现主共振和次共振[22]。由于不研究该系统的非线性特性，因此选取的激励频率很低，以避开共振频率。在实际工程结构中，由于加工精度问题、试验条件限制和复杂环境影响，机械系统的结构参数和材料参数都存在不确定性，使传统基于确定性模型计算得到的响应结果已经不能满足工程实际的需要，因此对机械系统进行不确定性分析具有重要的意义。其中，有一部分不确定性参数可以通过试验找出其概率分布，这种参数不确定性为随机不确定性。另一部分不确定性参数，难以用确定的随机分布来描述，这就造成众多认知不确定性存在于系统中。当系统同时存在随机不确定性和认知不确定性时，需要将这两种不确定性进行分离，以分析各种不确定性对总响应的贡献程度。为了便于分析，首先认为参数不具有时变性；然后针对该系统存在的混合不确定性，提出了随机和认知不确定性量化的置信区域法。

2 置信区域法

在t时刻，包含随机和认知不确定性质量块位移的函数可以表示为

x(t)=f(a|e)=f(a1,…,anA|e1,…,enE)

(5)

其中：x(t)为t时刻质量块位移；a=[a1,…,anA]为随机不确定性变量；e=[e1,…,enE]为认知不确定性变量。

为了书写简便，x(t)简写为x。Ξi为e中元素ei的可能的值，所有e的可能值的集合可以表示为

Ξ=Ξ1×Ξ2×…×ΞnE

(6)

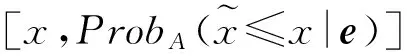
(7)

其中

(8)

选取不同的e值，将得到结果x不同的分布。因此，当e从集合Ξ中选取不同的值时，将得到关于结果x的一组认知不确定性分布。

下面主要讨论如下集合形式的不确定性结构

(9)

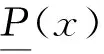
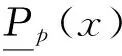
(10)

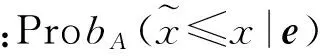
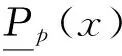
(11)

取q=0,当x=xd时，Prbq(x)=2.5%；取q=1,当x=xu时，Prbq(x)=97.5%。定义[xdxu]为t时刻质量块位移的95%置信区间，且当q∈[0 1]时，有以下特性：a.对于Prbq(xdq)=2.5%，有xdq≥xd；b.对于Prbq(xuq)=97.5%，有xu≥xuq。在时域分析中，每个时刻都能得到一个95%置信区间[xd(t)xu(t)]，所有时刻置信区间的上(下)边界即构成质量块位移响应的95%置信区域上(下)边界。

3 改进的双层循环蒙特卡罗法

目前，常采用双层循环蒙特卡罗法抽样技术[21]来处理同时存在随机和认知不确定性的问题。然而，传统的双层循环蒙特卡罗抽样方法只能处理输出结果为标量的系统(如系统固有频率，使用寿命等)，因此，笔者对双层循环蒙特卡罗抽样方法进行了一些修改，使其能够处理输出为时间响应的系统。

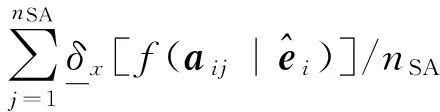
(12)

则xd≅min{xd1,…，xdnSE}

张连长:“别拦他!谁也别拦他!我看他想怎么样!路上我是你们带队,到了连队我是你们连长!想跟连长打架,反教了!”

(13)

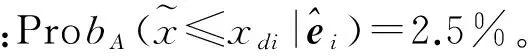
xu≅max{xu1,…，xunSE}

(14)

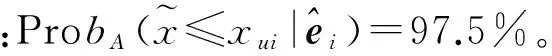
图2为改进的双层循环蒙特卡罗法抽样技术的主要步骤，具体为：

图2 改进的双层循环蒙特卡罗法抽样技术Fig.2 Improved double-loop Monte Carlo sampling

1) 选择处理认知不确定性的抽样数量M。当采用拉丁超立方抽样(latin hypercube sampling，简称LHS)进行抽样时，最小抽样数量M可以根据[21]M=m3+2进行估算，其中m为认知不确定性的数量。当m不是很大时，为了提高计算精度应该适当增大M。

2) 选择处理随机不确定性的抽样数量N。为了准确描述系统响应的分布，N一般要求较大。

3) 从每一个认知不确定性(区间参数)中选择一个样本。因为采用LHS进行抽样，所以选择的抽样数量M相对比较少。

4) 在给定认知不确定性样本点的条件下，从随机不确定性分布中选择一组样本。

5) 采用完整的抽样序列计算系统响应。

6) 判断随机不确定性的N个样本是否已经完成。如果否，回到步骤4)；如果是，继续步骤7)。

7) 基于随机不确定性计算得到的N个系统响应，求各时刻系统响应的95%(置信度2.5%～97.5%)置信区间。所有时刻置信区间上(下)边界即构成选定认知不确定性样本点情况下随机不确定性样本的95%置信区域上(下)边界。

8) 判断认知不确定性的M个样本是否已经完成。如果是，继续步骤9)，否则回到步骤3)。

9) 将M对置信区域上、下边界线画在同一张图上，以显示具有一定置信度的所有系统响应边界的全体。每一对边界线显示对应的每个认知不确定性样本点的系统响应的一个置信区域。

10) 对所有置信区域，分别找出上边界的最大值和下边界的最小值，该最大上边界和最小下边界围成的区域即为同时考虑随机和认知不确定性时的95%置信区域。

11) 将系统响应的最大上边界和最小下边界画在同一张图上，以显示混合不确定性的影响。

4 数值仿真

笔者仅考虑系统参数的不确定性，假设m,c,k和kf相互独立。对不确定性参数m,c,k和kf根据实验数据掌握情况分3种不确定性工况，分别研究质量块位移响应的不确定性分布。在工况1中参数m,c,k和kf属于随机不确定性，假设其服从正态分布，给定均值和方差。在工况2中,参数m,c,k和kf属于认知不确定性，给定分布区间。在工况3中,参数k和kf属于随机不确定性，假设其服从正态分布，给定均值和方差，而m和c属于认知不确定性，给定分布区间。这3种工况的具体取值如表1所示。由于仅考虑系统参数的不确定性，取Y=10，ω=1。初始时刻，质量块位移和速度都为0。

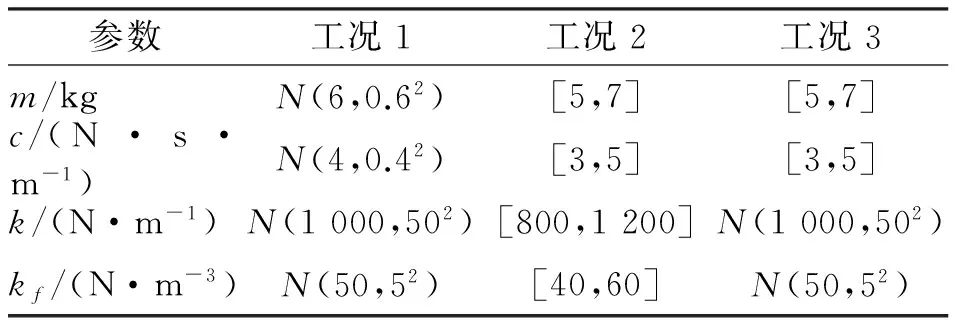
表1 不同工况下参数的不确定性取值

在工况1中，由于参数m，c，k和kf都属于随机不确定性，采用传统的蒙特卡罗抽样技术对其抽样1 000次。质量块位移的95%置信区域的边界如图3所示。在工况2中，由于参数m，c，k和kf都属于认知不确定性，给定参数的区间参数，所以得到的响应也是区间数。这里采用LHS抽样方法进行抽样1 000次，再将样本点分别代入动力学方程求响应。最后，求出响应的最大值和最小值，如图4所示。在工况3中,由于参数m和c属于认知不确定性，而k和kf属于随机不确定性，用改进的双层循环蒙特卡罗法抽样技术对该系统进行不确定性分析。外层循环对应于质量和阻尼的认知不确定性进行抽样，内层循环对应于线性刚度和非线性刚度的随机不确定性进行抽样。质量块位移的95%置信区域边界以及混合边界如图5所示。

图3 质量块位移的置信区域边界以及标准模型响应Fig.3 Statistics of mass block displacement: boundaries of confidence region and response of the nominal model

图4 质量块位移的响应区域边界以及标准模型响应Fig.4 Statistics of mass block displacement: boundaries of the response and response of the nominal model

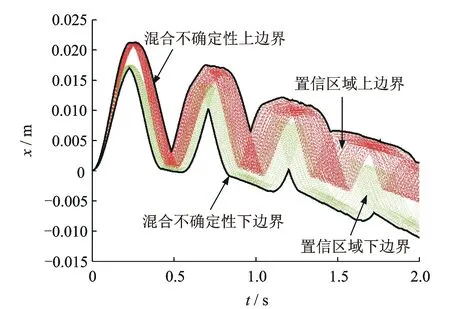
图5 质量块位移的置信区域边界以及混合边界Fig.5 Statistics of mass block displacement: boundaries of confidence region for aleatory uncertainty and mixed-uncertainty

由图3～图5可知，工况1中参数为随机不确定性，因为假设参数为正态分布，所以能够得到每个时刻质量块位移的概率分布，从而得到每个时刻质量块位移的95%置信区间和质量块位移的95%置信区域。工况2中参数为认知不确定性，因为假设参数为区间数，所以同样采用区间数即可描述质量块位移的不确定性。工况3中，由于参数同时存在随机和认知不确定性，无法用传统的方法进行不确定性分析，采用改进的双层循环蒙特卡罗法抽样技术对其进行不确定性分析，得到每个时刻质量块位移的概率边界，再由概率边界得到95%置信区间,进而得到95%置信区域。可见，考虑参数存在随机不确定性或混合不确定性时，得到质量块位移的响应为置信区域，该响应结果存在一定的置信度。考虑参数存在认知不确定性时，得到质量块位移的响应区域。通过图5可以看出,仅考虑随机不确定性所得到的系统响应的95%置信区域包含于混合不确定性的95%置信区域内。

5 结束语

为了对同时存在随机和认知不确定性的非线性机械系统进行分析，笔者提出了随机和认知不确定性量化的置信区域法。该方法不仅能够在整个时间域内单独分析随机不确定性和认知不确定性对响应的影响，而且还能够得到混合不确定性对响应的影响。由数值仿真可知，同时考虑参数的随机和认知不确定性得到的置信区域边界比只考虑随机不确定性时的边界要宽。因此，在对非线性机械系统进行分析时考虑这两种不确定性的影响，将使系统工作时更加安全。

[1] Schu⊇ller G I. On the treatment of uncertainties in structural mechanics and analysis[J]. Computers & Structures, 2007,85(5):235-343.

[2] Li L, Sandu C. On the impact of cargo weight, vehicle parameters, and terrain characteristics on the prediction of traction for off-road vehicles[J]. Journal of Terramechanics, 2007,44(3):221-238.

[3] Sandu A, Sandu C, Ahmadian M. Modeling multibody systems with uncertainties. Part I: theoretical and computational aspects[J]. Multibody System Dynamics, 2006,15(4):373-395.

[4] Sandu C, Sandu A, Ahmadian M. Modeling multibody systems with uncertainties. Part II, numerical applications[J]. Multibody System Dynamics, 2006,15(3):241-262.

[5] An D, Choi J, Schmitz T L, et al. In situ monitoring and prediction of progressive joint wear using Bayesian statistics[J]. Wear, 2011,270(11):828-838.

[6] Hofer E, Kloos M, Krzykacz-Hausmann B, et al. An approximate epistemic uncertainty analysis approach in the presence of epistemic and aleatory uncertainties[J]. Reliability Engineering & System Safety, 2002,77(3):229-238.

[7] Huang Hongzhong, Zhang Xudong. Design optimization with discrete and continuous variables of aleatory and epistemic uncertainties[J]. ASME Journal of Mechanical Design, 2009,131(3):310061-310068.

[8] 张保强，陈国平，郭勤涛.不确定性热弹耦合梁的固有振动分析[J].振动与冲击,2012,31(19):160-164.

Zhang Baoqiang, Chen Guoping, Guo Qintao. Free vibration analysis of a thermoelastic coupled beam with material uncertainty[J]. Journal of Vibration and Shock, 2012,31(19):160-164. (in Chinese)

[9] 赵宽，陈建军，阎彬，等.含随机参数的多体系统动力学分析[J].力学学报,2012,44(4):802-806.

Zhao Kuan, Chen Jianjun, Yan Bin, et al. Dynamic analysis of multibody systems with probabilistic parameters[J]. Chinese Journal of Theoretical and Applied Mechanics, 2012,44(4):802-806. (in Chinese)

[10]曾开春，向锦武.高超声速飞行器飞行动力学特性不确定分析[J].航空学报,2012,33(4): 1-11.

Zeng Kaichun, Xiang Jinwu. Flight dynamic characteristics of hypersonic vehicles with uncertain parameters[J]. Acta Aeronautica et Astronautica Sinica, 2012,33(4):1-11. (in Chinese)

[11]Nilsson N J. Probabilistic logic[J]. Artificial Intelligence, 1986,28(1):71-87.

[12]Oberkampf W L, Helton J C, Joslyn C A, et al. Challenge problems: uncertainty in system response given uncertain parameters[J]. Reliability Engineering & System Safety, 2004,85(1):11-19.

[13]Ross T J. Fuzzy logic with engineering applications[M]. 2nd ed. New York: Wiley, 2004:6-20.

[14]Merlet J P. Solving the forward kinematics of a Gough-type parallel manipulator with interval analysis[J]. The International Journal of Robotics Research, 2004,23(3):221-235.

[15]杜永峰，李万润，李慧.基于测量数据不确定性的结构参数识别[J].振动、测试与诊断,2012,32(4):629-633.

Du Yongfeng, Li Wanrun, Li Hui. Structural parameters identification based on uncertainty of measurement data[J]. Journal of Vibration, Measurement & Diagnosis, 2012,32(4):629-633. (in Chinese)

[16]Beynon M, Curry B, Morgan P. The Dempster-Shafer theory of evidence: an alternative approach to multicriteria decision modelling[J]. Omega, 2000,28(1):37-50.

[17]Dubois D. Possibility theory and statistical reasoning[J]. Computational Statistics & Data Analysis, 2006,51(1):47-69.

[18]Helton J C, Johnson J D, Oberkampf W L, et al. Representation of analysis results involving aleatory and epistemic uncertainty[J]. International Journal of General Systems, 2010,39(6):605-646.

[19]Sentz K, Ferson S. Probabilistic bounding analysis in the quantification of margins and uncertainties[J]. Reliability Engineering & System Safety, 2011,96(9):1126-1136.

[20]Helton J C. Quantification of margins and uncertainties: conceptual and computational basis[J]. Reliability Engineering & System Safety, 2011,96(9):976-1013.

[21]Oberkampf W L, Roy C J. Verification and validation in scientific computing[M]. New York: Cambridge University Press, 2010:606-610.

[22]胡海岩.应用非线性动力学[M].北京:航空工业出版社,2000:68-72.

10.16450/j.cnki.issn.1004-6801.2015.05.017

*重庆大学科研启动基金资助项目(0240001104412)

2013-10-25；

2013-11-21

TB114; TH113

孙东阳，男，1985年6月生，博士、讲师。主要研究方向为多体系统动力学建模及控制。曾发表《Model reduction of a multibody system including a very flexible beam element》(《Journal of Mechanical Science and Technology》2014,Vol.28,No.28)等论文。 E-mail：sundongyang@cqu.edu.cn