(周立)

Department of Mathematics,Huzhou University,Huzhou 313000,China

E-mail:lfzhou@hutc.zj.cn

ON THE BOUNDEDNESS AND THE NORM OF A CLASS OF INTEGRAL OPERATORS∗

Lifang ZHOU(周立芳)

Department of Mathematics,Huzhou University,Huzhou 313000,China

E-mail:lfzhou@hutc.zj.cn

integral operators;sufcient condition;necessary condition;operator norm; hypergeometric functions

2010 MR Subject Classifcation47B38;47G10

1 Introduction

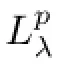
It is well known that the weighted harmonic Bergman projection

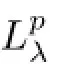
was discussed while studying the Toeplitz operator on harmonic Bergman space,see[8].And see[9]for the Berezin-type transform with λ=0.Therefore,to give the boundedness and the norm of the integral operators,such as Sλand Berezin-type operator Bλdefned above,we need to consider such class integral operators

where a,b,c∈R.

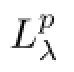
(3)Ta,b,cis bounded on L∞,if and only if

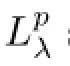
Corollary 1.2Suppose a,b,c and λ∈R,and c=n+a+b.

(i)Let 1＜p＜∞,a,b,λ be such that

Then we have

(ii)Suppose p=1.If a,b,λ are such that

then we have

If a,b,λ are such that

then we have

(iii)Suppose p=∞,a＞0,b＞-1.If b≤a-n or b≥a-2,then

If a-n＜b＜a-2,then

2 Preliminaries

A number of hypergeometric functions will appear throughout.We use the classical notation2F1(α,β;γ;z)to denote

with γ/=0,-1,-2,···,where

And the hypergeometric series in(2.1)converges absolutely for all the value of|z|＜1.

We list a few formulas for easy reference(see[26,Chapter II]):

The following integral formulas concerning the hypergeometric functions are signifcant for our main results.

Lemma 2.1([6,Lemma 2.2])For γ∈R and α＞-1,we have

Corollary 2.2(Forelli-Rudin estimates,see[3,Lemma 4.4])Let α＞-1 and β∈R. Then for any x∈Bn,

where a(x)≈b(x)means that the ratio a(x)/b(x)has a positive fnite limit as|x|→1-.

Lemma 2.3([6,Lemma 2.1])Suppose Reλ＞0,Reδ＞0 and Re(λ+δ-α-β)＞0. Then

Lemma 2.4Let α＞0,β＞0,γ∈R,and n+α+β-2γ-1＞0,we have

ProofUsing Lemma 2.1 in the inner integral of(2.8),we have

Then(2.7)shows the result.

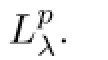
Lemma 2.5([27,Theorem 3.6])Suppose that(X,µ)is a σ-fnite measure space and K(x,y)is a nonnegative measurable function on X×X and T the associated integral operator

Let 1＜p＜∞and 1/p+1/q=1.If there exist positive constants C and a positive measurable function u on X such that

for almost every x in X,and

for almost every y in X,then T is bounded on Lp(X,µ)with‖T‖≤C.

3 Proof of Theorem 1.1

The proof of Theorem 1.1 will be divided into two steps.

Step IProve(2)and(3)in Theorem 1.1.Let T∗

a,b,cdenote the adjoint operator of Ta,b,c, and

Since

is a fnite number by Lemma 2.1.From(2.6),we see that

which gives case(2).And case(3)can be obtained in the same way as case(2).

Step IIProve(1)in Theorem 1.1.Suppose 1＜p＜∞,and q is the conjugate number of p such that 1/p+1/q=1 in this step.

we will take

where

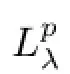
With α=b+1+(σ-(λ+1))/p,β=a+σ/q+(λ+1)/p,γ=c/2,applying Lemma 2.4 to the left-hand of last inequality,we frstly get

Then the arbitrariness of σ＞0 implies

When c=n+a+b,by(2.8),the inequality(3.2)is to be that

Letting σ→0+in the last inequality,we can see that the limit

is a fnite non-negative real number.Thus,we can conclude that-pa＜λ+1＜p(b+1)since the limit of the denominator,

is a fnite non-negative real number under the condition of(3.3).

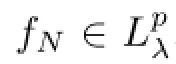
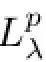
Using Lemma 2.1 and(2.3),we frst calculate the integral

where

Thus,applying(2.4),we have

Similar argument gives

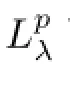
4 Proof of Corollary 1.2

whose monotonicity implies the result of(ii)in Corollary 1.2.And the same line as(ii)gives (iii)in Corollary 1.2.?

[1]Miao J.Reproducing kernels for harmonic Bergman spaces of unit ball.Monatsh Math,1998,125:25-35

[2]Coifman R,Rochberg R.Representation theorems for holomorphic and harmonic functions in Lp. Ast´erisque,1980,77:11-66

[3]Ren G B.Harmonic Bergman spaces with small exponents in the unit ball.Collect Math,2002,53(1): 83-98

[4]Jevti`c M,Pavlovi`c M.Harmonic Bergman functions on the unit ball in Rn.Acta Math Hungr,1999,85: 81-96

[5]Choe B R,Koo H,Nam K.Optimal norm estimate of operators related to the harmonic bergman projection on the ball.Tohoku Math J,2010,62(2):357-374

[6]Liu C W,Zhou L F.Norm of an integral operator related to the harmonic Bergman projection.Integr Equ Oper Theory,2011,69:557-566

[7]Liu C W,Per¨al¨a A,Zhong Y.A higer-dimensional analogue of Hilbert’s inequality.Preprint

[8]Liu C W.A“deformation estimate”for the toeplitz operators on harmonic Bergman spaces.Proc Amer Math Soc,2007,135:2867-2876

[9]Liu C W.Iterates of a Berezin-type transform.J Math Anal Appl,2007,329:822-829

[10]Kures O,Zhu K.A class of integral operators on the unit ball of Cn.Integr Equ Oper Theory,2006,56: 71-82

[11]Forelli F,Rudin W.Projections on spaces of holomorphic functions in balls.Indiana Univ Math J,1974, 24:593-602

[12]Dostani´c M.Norm of the Berezin transform on Lpspaces.J d’Analyse Math,2008,104:13-23

[13]Liu C W,Zhou L F.On the p norm of the Berezin transform.Illinois J Math,2012,56(2):497-505

[14]Zhu K H.A sharp norm estimate of the Bergman projection on Lpspaces.Contemporary Math,2006,404: 199-205

[15]Dostani´c M.Two sided norm estimate of the Bergman projection on Lpspaces.Czechoslovak Math J,2008, 58(133):569-575

[16]Per¨al¨a A.On the optimal constant for the Bergman projection onto the Bloch space.Ann Acad Sci Fenn Math,2012,37:245-249

[17]Per¨al¨a A.Bloch space and the norm of the Bergman projection.Ann Acad Sci Fenn Math,2013,38: 849-853

[18]Kalaj D,Markovi´c M.Norm of the Bergman projection.Math Scand,2014,115(1):143-160

[19]Liu C W,Zhou L F.On the p-norm of an integral operator in the half plane.Canad Math Bull,2013, 56(3):593-601

[20]Koo H,Nam K,Yi H.Norm estimation of the harmonic Bergman projection on half-spaces.J Math Soc Japan,2009,61:225-235

[21]Pott S,Reguera M.Sharp B´ekoll´e estimates for the Bergman projection.J Funct Anal,2013,265(12): 3233-3244

[22]Charpentier P,Dupain Y,Mounkaila M.Estimates for weighted Bergman projections on pseudo-convex domains of fnite type in Cn.Complex Var Elliptic Equ,2014,59(8):1070-1095

[23]Dostani´c M,Zhu K.Integral operators induced by the Fock kernel.Integr Equ Oper Theory,2008,60(2): 217-236

[24]Dostani´c M.Norm estimate of the Cauchy transform on Lp(Ω).Integr Equ Oper Theory,2005,52(4): 465-475

[25]Hu G E,Zhu Y P.Weighted norm inequalities for the commutators of multilinear sigular integral operators. Acta Math Sci,2011,31B(3):749-764

[26]Erd´elyi A,Magnus W,Oberhettinger F,et al.Higher Transcendental Functions,Vol I.New York:McGraw-Hill,1953

[27]Zhu K H.Operator Theory in Function Spaces.2nd ed.Providence:Amer Math Soc,2007

∗Received May 20,2014;revised November 27,2014.Supported by the National Natural Science Foundation of China(11426104,11271124,11201141,11301136,and 61473332),Natural Science Foundation of Zhejiang province(LQ13A010005,LY15A010014)and Teachers Project of Huzhou University(RP21028).