D´epartement de Math´ematiques,Facult´e des Sciences de Sfax,Universit´e de Sfax, Route de soukra Km 3.5,B.P 1171,3000,Sfax,Tunisie

E-mail:charf.salma@yahoo.fr;rahali.sassia@gmail.com

ON A CHARACTERIZATION OF THE S-ESSENTIAL SPECTRA OF THE SUM AND THE PRODUCT OF TWO OPERATORS AND APPLICATION TO A TRANSPORT OPERATOR∗

Salma CHARFISassia RAHALI

D´epartement de Math´ematiques,Facult´e des Sciences de Sfax,Universit´e de Sfax, Route de soukra Km 3.5,B.P 1171,3000,Sfax,Tunisie

E-mail:charf.salma@yahoo.fr;rahali.sassia@gmail.com

In this paper,we develop some operational calculus inspired from the Fredholm operator theory to investigate the S-essential spectra of the sum and the product of two operators acting on a Banach space.Furthermore,we apply the obtained results to determine the S-essential spectra of an integro-diferential operator with abstract boundary conditions in L1([-a,a]×[-1,1])(a＞0).

Fredholm operator;Fredholm perturbation;S-essential spectra;transport operator

2010 MR Subject Classifcation47A13

1 Introduction

Let X and Y be two Banach spaces.We denote by L(X,Y)(resp.C(X,Y))the set of all bounded(resp.closed,densely defned)linear operators from X into Y and we denote by K(X,Y)the subspace of compact operators from X into Y.For A∈C(X,Y),we write D(A)⊂X for the domain,N(A)⊂X for the null space and R(A)⊂Y for the range of A. The nullity,α(A),of A is defned as the dimension of N(A)and the defciency,β(A),of A is defned as the codimension of R(A)in Y.

Let S∈L(X,Y)and A∈C(X,Y),we defne the S-resolvent set of A by:

and the S-spectrum of A by:

When S=I,ρI(A)=ρ(A)and σI(A)=σ(A),where ρ(A)and σ(A)are respectively the resolvent and the spectrum of the operator A.

The set of Fredholm operators from X into Y is defned by

Φ(X,Y):=?A∈C(X,Y)such that α(A)＜∞,β(A)＜∞and R(A)is closed in Y?.For A∈Φ(X,Y),the number i(A):=α(A)-β(A).If X=Y then L(X,Y),C(X,Y),K(X,Y), and Φ(X,Y)are replaced by L(X),C(X),K(X),and Φ(X)respectively.A complex number λ is in ΦA,Sif λS-A is in Φ(X).When S=I,the set ΦA,Iis denoted by ΦA.

In this paper we are mainly concerned with the following essential spectra:

where ρw,S(A):={λ∈ΦA,Ssuch that i(λS-A)=0}and ρb,S(A)denotes the set of those λ∈ρw,S(A)such that all scalars near λ are in ρS(A).

Note that these sets satisfy the following inclusions

Remark 1.1(i)If S=I,we recover the usual defnition of the essential spectra of a closed densely defned linear operator A,that is,the subset σe,I(·)is the Wolf essential spectrum[9,24],σw,I(·)is the Schechter essential spectrum[17,18]and σb,I(·)denotes the Browder essential spectrum[9,15].

(ii)The notion of S-essential spectrum σe,S(.)was introduced in[7]as a generalization of the usual notion of Wolf essential spectrum.

(iii)Note that even if S is invertible,we haven’t σi(A)=σi,S(A),i=e,w,b.For example, if X is a fnite dimension space and S is an invertible operator such that σ(S){1}is not empty, then σS(S)={1},which implies that σS(S)/=σ(S).

This paper is devoted to some recent mathematical developments which cover several topics including Fredholm perturbation and spectral theory of operator pencils.These topics play a crucial role in many branches of mathematics and in numerous applications as they are intimately related to the stability of the underlying physical systems.

In fact,numerous mathematical and physical problems lead to operator pencils,λS-A (operator-valued functions of a complex argument),(see,for example,[13,22]).The spectral theory of these operators has recently attracted the attention of many mathematicians[3,10, 11].More precisely,in[11],A.Jeribi,N.Moalla and S.Yengui studied the S-essential spectra of closed densely defned linear operators and gave practical criteria that guarantee the invariance of various S-essential spectra for perturbed linear operators and improve many known ones in the literature.

The studies of[11]were pursued by F.Abdmouleh,A.Ammar and A.Jeribi in[3]to develop some interesting and basic properties about S-essential spectra and investigate the S-Browder essential spectra of bounded linear operators on a Banach space X.Moreover,they extended the results of F.Abdelmouleh and A.Jeribi given in[1]to various types of S-essential spectra.

Inspired by[21],F.Abdmouleh,S.Charfand A.Jeribi were concerned in[2]with the case where A∈C(X)and B∈L(X)and which commute modulo the Fredholm perturbations and they obtain under some conditions,

Our central interest in this paper is to address the characterization of the sum and the product of some S-essential spectra of two operators and establish,in particular,some conditions thatwe must impose on the operators A∈C(X),S∈L(X)and B∈L(X),in order to improve and generalize some results recently obtained by the authors in[2].In fact,we prove that

In particular,if S=I,then those obtained in[2]will be special cases of those obtained in this paper.

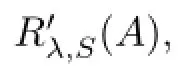
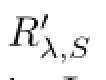
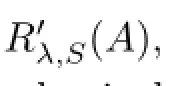
In the last section,we will apply the results obtained in Section 4 to describe the S-essential spectra of the following integro-diferential operator with abstract boundary conditions,in the Banach space X1:=L1((-a,a)×(-1,1),dxdξ),0＜a＜+∞.

where THis defned by

where σ(·)and η(·)are in L∞(-1,1),κ(·,·,·)is a measurable function,and H is the boundary operator connecting the outgoing and the incoming fuxes.It describes the transport of particles (neutrons,photons,molecules of gas,etc)in a slab with thickness 2a.The function φ(·,·) represents the number density of gas particles having the position x and the direction cosine of propagation ξ(see Section 5 for more details).

Our paper consists of four sections.In Section 2,we present some basic notations and results connected to the main body of the paper.In Section 3,we develop some operationalcalculus that are needed in Section 4 to give a characterization of the S-essential spectra of the sum of two operators.Section 5 is devoted to the application of the obtained results on a transport operator with abstract boundary conditions in L1-spaces.

2 Preliminary Results

In order to state our main results in the third section,let us recall some defnitions,notations and basics on Fredholm perturbations.

Defnition 2.1Let X and Y be two Banach spaces and let F∈L(X,Y),F is called a Fredholm perturbation if T+F∈Φ(X,Y)whenever T∈Φ(X,Y).

The set of Fredholm perturbations is denoted by F(X,Y).If X=Y,F(X):=F(X,X)is a closed two-sided ideal of L(X).

Defnition 2.2Let X and Y be Banach spaces.An operator A∈L(X,Y)is called strictly singular if,for every infnite-dimensional subspace M of X,the restriction of A to M is not a homeomorphism.The family of strictly singular operators from X to Y is denoted by S(X,Y).

The concept of strictly singular operators was introduced in the pioneering paper by T. Kato[12]as a generalization of the notion of compact operators.If X=Y,the strictly singular operators on X will be denoted by S(X):=S(X,X).For a detailed study of the properties of strictly singular operators,we refer to[8,12].Note that S(X)is a closed two-sided ideal of L(X).

Defnition 2.3Let X and Y be Banach spaces.An operator A∈L(X,Y)is said to be weakly compact if A(U)is relatively weakly compact in X for every bounded subset U⊂X. We denote the family of weakly compact operators from X to Y by W(X,Y)and if X=Y, W(X,X):=W(X).

Remark 2.4(i)In general,we have

Note that the class of weakly compact operators in L1-spaces is nothing else than the family of strictly singular operators on L1-spaces(see[16,Theorem 1]).Therefore,it follows from the above inclusion that any weakly compact operator in L1-spaces is a Fredholm perturbation.

(ii)The set of Riesz operators denoted R(X)and characterized in[4]by:

is not an ideal of L(X)(see[5]).In[18],it was proved that F(X)is a largest closed two-sided ideal contained in R(X).

Lemma 2.5(see[2])Let A∈C(X,Y).Suppose that there are operators A1,A2∈L(Y,X),F1∈F(X)and F2∈F(Y)such that

Then A∈Φ(X,Y).

3 The Operational Calculus

In this section,we establish some operational calculus which extend and improve some results obtained in[20,23].We begin with some defnitions and then continue with some lemmas and propositions.

Defnition 3.1A bounded operator B is called a quasi-inverse of the closed operator A if

(i)R(B)⊂D(A)and AB=I+K1,K1∈K(X).

(ii)BA=I+K2,K2∈K(X).

Let A∈C(X)be a closed operator such that ΦA,Sis not empty and S∈L(X)a non null bounded linear operator.By virtue of[11,Proposition 2.1],the following lemma holds:

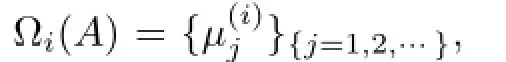
Let λibe a fxed point in{Φi,S(A)Ωi(A)}.Since α(λiS-A)＜∞,R(λiS-A)is closed and β(λiS-A)＜∞,then there exist a closed subspace Xiand a subspace Yisuch that dimYi=β(λiS-A)satisfying

Now,let P1ibe the projection of X onto N(λiS-A)along Xiand let P2ibe the projection of X onto Yialong R(λiS-A).P1iand P2iare bounded fnite rank operators.It follows from [17]that(λiS-A)|D(A)∩Xihas a bounded inverse,Ai,

Let Tithe bounded operator defned by:Tix:=Ai(I-P2i)x satisfying:

Hence,Tiis a quasi-inverse of(λiS-A).

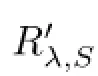
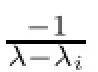
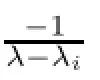
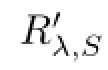
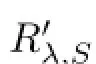
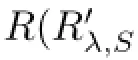
On the other hand,the equality STi=TiS allows us to write

This ends the proof.

Theorem 3.7Let L1and L2be two diferent choices of R′λ,S(A).Then,L1-L2is a bounded fnite rank operator.

ProofSince L1and L2are two bounded inverses of(λS-A),then the following equalities hold:

where F1and F2are two bounded fnite rank operators.In fact,we have

which implies that

is a bounded fnite rank operator.

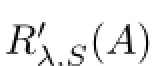
Lemma 3.9The following inclusion holds

ProofLet λ∈Ωi(A).Since α(λS-A)＞α(λiS-A),then there exists x∈X such that x/=0 and x∈N(λS-A)∩Xiwhere Xiis the closed complement of N(λiS-A)chosen in the construction of Ti.Thus

and we get

Remark 3.10depends on the choice of Ti.

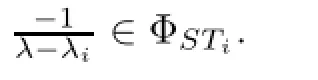
ProofFirst of all,let us establish the following equalities:

Now,suppose that λ∈ΦA,S,then using[17,Theorem 2.8],we deduce that A-λS+(λλi)SP1i∈Φ(X).Since(λiS-A)∈Φ(X),by virtue of[17,Theorem 3.4],we infer that

Now,[17,Theorem 2.8]assures that A-λS∈Φ(X)and hence we deduce that λ∈ΦA,S.?

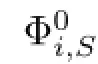
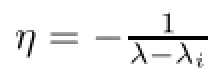
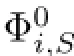
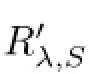
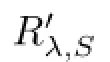
If λi∈ρS(A),then Ti=(λiS-A)-1and we get

Similarly,we prove that Ti[(λ-λi)STi+I]-1(λS-A)=I.?

Next,we will develop an operational calculus which will enlarge the set of functions and can be applied to the closed operator A.Our results generalize the ones obtained in[20].

If f(λ)is a complex valued analytic function of a complex variable,we denote by Δ(f)the domain of analyticity of f.

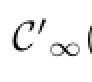
1.σe,S(A)⊂Δ(f),

2.Δ(f)contains a neighborhood of∞and f is analytic at∞.

Defnition 3.15A set D in the complex plane is called a Cauchy domain if the following conditions are satisfed:

1.D is open,

2.D has a fnite number of components,the closures of any two of which are disjoint,

3.the boundary of D is composed of a fnite positive number of closed rectifable Jordan curves,no two of which intersect.

In what follows,we assume that the operator S has a bounded inverse.

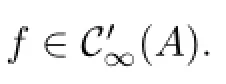
where D is unbounded Cauchy domain such that

1.σe,S(A)⊂D,

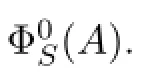
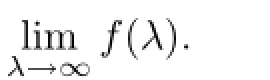
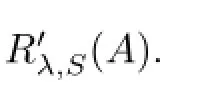
iii)The existence of D satisfying conditions 1 and 2 follows from[23,Theoreme 3.3]by taking σe,S(T)as the closed set and choosing the open set as intersection of Δ(f)and the exterior sufcient small circle with center in ΦA,S(this last precaution being necessary only in case Δ(f)is the entire plane).

v)All the members of G(A)are bounded.

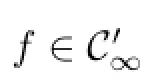
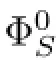
ProofThe lemma follows from Theorem 3.12 and the compactness of C(D).?

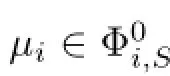
2.µi∈D,

Then

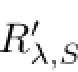
Therefore,we shall assume that λi/∈D and we have

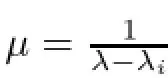
Z

Now,we observe that

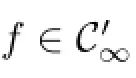
ProofBy defnition

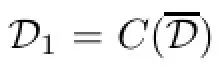
Defnition 3.22Suppose that A∈L(X).By C′(A)we mean the family of all analytic functions f(λ)such that σe,S(A)⊂Δ(f).

Defnition 3.23Let A∈L(X)and f∈C′(A),we defne the class of operators G∗(A)as follows:

where D is a bounded Cauchy domain such that

1.σe,S(A)⊂D,

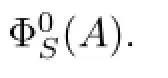
Defnition 3.24Let A∈L(X)and f∈C′(A).By f∗(A)we mean an arbitrary operator in the set G∗(A).

Remark 3.25Let A∈L(X)and f∈C′(A).By the same ways as in proof of[23,Theorem 4.1],we can easily show that f∗(A)is an element of L(X)which is independent of D.

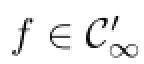
ProofLet C be a circle of radius r,so chosen that D lies in the interior of C.C and the region exterior to it lie in Δ(f),and r is greater than the spectral radius of S-1A.

The integral on the right is equal to

Moreover,for|λ|＞‖S-1A‖,we have

Now,one can check easily that the frst integral in(3.3)tends to zero as r→∞.The second integral have the value-f(∞)I,by the integrating the series(3.4)termwise.?

Theorem 3.27Let A∈L(X),and let f(λ)=1.Then f∗(A)=I+K,K∈K(X).

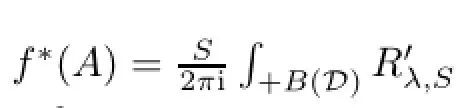
Theorem 3.28Let A∈L(X),and let f(λ)=λ.Then f∗(A)=AS-1.

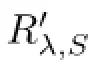
Reasoning as the same way as in[20,Lemma 7.5],we show that the following lemma holds true:

Lemma 3.29Let λ andµbe in ΦA,S.Then,

where K is a compact operator which depends analytically onµand λ.

Thanks to this lemma,we can prove the following result which is useful in the end of the next section and it can be proved in the same way as in Lemma 7.6 in[20]:

Lemma 3.30Let f,g∈C′(A).Then

where K∈K(X).

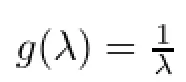
4 Main Results

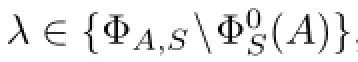
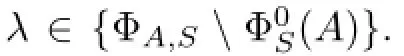
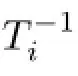
Lemma 4.2(see[2])Let A∈Φ(X),B∈L(X)and F∈F(X).Suppose that AB|V=F|Vwhere V is a dense subspace of X.Then B∈F(X).

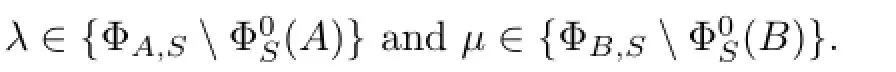
Then there exists a Fredholm perturbation F depending analytically on λ andµsuch that

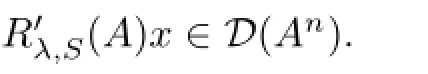
Now,let x∈Vλ,then we have

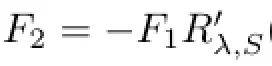
Hence,we get

where K2=K1B∈K(X).

This makes us conclude that

where F4∈F(X).In fact,the Eq.(4.1)holds for all x∈Vλ,then by virtue of Lemma 4.2,we have

where F5∈F(X).In the same ways,we prove that

where K3∈K(X).On the other hand,

where Ki∈K(X)for i=4,5,6,7 and Fi∈F(X)for i=6,7.

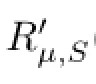
Theorem 4.4Let A∈C(X),B,S∈L(X)such that SB=BS.Suppose that there exist a positive integer n and a Fredholm perturbation F1,such that S,B:D(An)→D(A)and satisfying

Then

(i)σe,S(A+B)⊆σe,S(A)+σe,S(B).

If σe,S(A)is empty,then σe,S(A)+σe,S(B)is also empty set.

(ii)If in the addition Cσe,S(A),Cσe,S(B)and Cσe,S(A+B)are connected,ρS(A)and ρS(A+B)are nonempty sets,then

(iii)Moreover,if Cσw,S(A),Cσw,S(B)and Cσw,S(A+B)are connected,ρS(A)and ρS(A+B)are nonempty sets,then

Proof(i)Obviously,the theorem is clearly true if we suppose that σe,S(A)+σe,S(B)is the entire complex plane.Hence,we shall assume in the next that σe,S(A)+σe,S(B)is not the entire plane.

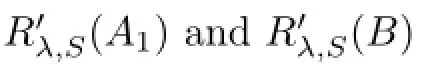
Since σe,S(A)is closed and σe,S(B)is compact,then there exists an open set U⊃σe,S(B) such that B(U),the boundary of U is bounded and when λ∈U,(γ-λ)∈ΦA,S.

Therefore σe,S(B)⊂U⊂ΦA1,S.The use of[23,Theorem 3.3]guarantees the existence a bounded Cauchy domain D such that σe,S(B)⊂D⊂U.

Now,let us defne the operators M1and M2as follows:

Our aim in the next is to prove that γ∈ΦA+B,S.From Lemma 2.5,it remains to fnd two Fredholm perturbations F1and F2such that

Now,writing the operator γS-B-A as follows:

we get

Using Theorem 3.27,we deduce that

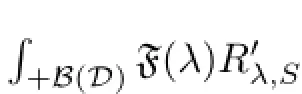
Applying Lemma 4.3,we get

where F(λ)is a Fredholm perturbation,then the second integral of equation(4.2)is equal to

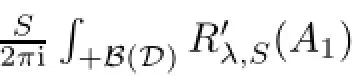
By a similar argument we obtain

Therefore,Lemma 2.5 enables us to deduce that(γS-B-A)∈Φ(X)and we can conclude that

(ii)-(iii)These assertions follow immediately from[11,Lemma 2.1].?

Theorem 4.5Let A∈C(X),B∈L(X)∩Φ(X)and S∈L(X).If SB=BS and there exist a Fredholm perturbation F,such that S,B:D(A)→D(A)and satisfying

Then BA is closable and

(i)

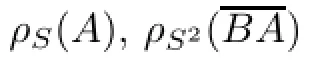
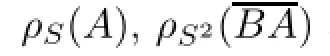
Proof(i)Since the operator F is bounded and the restriction of the operator AB on D(A)is closable,then BA is closable.

Furthermore it is clear that 0/∈σe,S(B)and σe,S(B)is not empty,so the theorem is clearly true if σe,S(A)=C and we will assume in the next that σe,S(A)/=C.

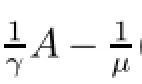
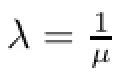
Let us defne the operators M1and M2as follows

Since R(M1)⊂D(A),the operator(γS-BA)M1is well defned and we have

moreover

Then

The frst part of the integral can be written as follows:

Since 0/∈D,then the use of Remark 3.31 allows us to deduce that

where Ki∈K(X),i=1,2,3.

The second part of the integral can also be written as:

where K4∈K(X)and Fi∈F(X),i=1,2,3.

where Ki∈K(X),i=5,6 and Fi∈F(X),i=5,6,7,8,9.

Now,to show the second inclusion,we will prove that(γS2-AB)∈Φ(X).Since R(M1)⊆D(A) and ABx=BAx+Fx,∀x∈D(A),we obtain

where Fi∈F(X),i=10,11.Moreover,we have

where F12∈F(X).Therefore,(γS2-AB)∈Φ(X)and this shows that

(ii)-(iii)These assertions follow immediately from[11,Lemma 2.1].?

5 Application to Transport Operator

In this section,we will study the S-essential spectra of a transport operator with abstract boundary conditions.

Let

We consider the following integro-diferential operator with abstract boundary conditions:

THis the streaming operator defned by:

where W is the space defned by

and σ(.)∈L∞(-1,1).ψ◦,ψirepresent,respectively,the outgoing and the incoming fuxes related by the boundary operator H(“◦”for the outgoing and“i”for the incoming)and given by

and K is a bounded operator defned by

where the kernel κ:(-a,a)×(-1,1)×(-1,1)→R is assumed to be measurable such that Kψ∈X1for all ψ∈X1.Note that the operator K is a bounded linear operator defned on X1.

respectively equipped with the norms

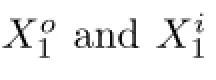
The object of this part is to determine the S-essential spectra of the operator AH,where S is the invertible operator defned by

where η(.)∈L∞(-1,1).

Notice that the collision operators K defned in Equation(5.1),acts only on the velocity ξ′,so x may be seen,simply,as a parameter in[-a,a],then,we will consider K as a function

In the sequel,we will make the following assumption introduced in[14]:

Defnition 5.1A collision operator in the form(5.1)is said to be regular on X1if it satisfes the assumptions(H1).

Lemma 5.2(see[11])If κ(x,ξ,ξ′)defnes a regular operator,then(λS-TH)-1K is weakly compact on X1.

Remark 5.3In[11],it is shown under assumption(H1)that:

Theorem 5.4Suppose that the collision operator K satisfes the hypothesis(H1)and the boundary operator H∈S(X1),then

ProofLet λ∈ρS(TH)such that rσ((λS-TH)K)＜1(rσ(.)the spectral radius).For such λ,the equation(λS-TH-K)φ=ψ may be transformed into

and so,

Therefore,we have λ∈ρS(TH)∩ρS(AH)and(λS-AH)-1=C+(λS-TH)-1,where

The regularity of K and the use of Lemma 5.2 make us conclude that C(λS-TH)-1-(λS-TH)-1C is weakly compact on X1.Therefore,this operator is a Fredholm perturbation.

It is easy now to check that all hypotheses of Theorem 4.4 are satisfed,then

On the one hand,we deduce from the regularity of K that SC is a Riesz operator,hence σi,S-1(C)={0},i=e,w,b.On the other hand,combining[3,Theorem 4.1]together with Remark 5.3,we obtain

[1]Abdlmouleh F,Jeribi A.Gustafson,Weidmann,Kato,Wolf,Schechter,Browder,Rakocevic and Schmoger essential spectra of the sum of two bounded operators.Math Nachr,2011,284:166-176

[2]Abdmouleh F,CharfS,Jeribi A.On a characterization of the essential spectra of the sum and the product of two operators.J Math Anal Appl,2012,386(1):83-90

[3]Abdmouleh F,Ammar A,Jeribi A.Stability of the S-essential spectra on a Banach space.Math Slovaca, 2013,63(2):299-320

[4]Aiena P.Riesz operators and perturbation ideals.Note di Matematica,1989,9(1):1-27

[5]Caradus S R.Operators of Riesz type.Paci J Math,1966,18:61-71

[6]Dautray R,Lions J L.Analyse Mat´ematique et Calcul Num´erique.Vol 9.Masson:Paris,1988

[7]Faierman M,Mennicken R,M¨oller M.A boundary eigenvalue problem for a system of partial diferential operators occuring in magnetohydrodynamics.Math Nachr,1995,173:141-167

[8]Gohberg I C,Markus A S,Feldman I A.Normally solvable operators and ideals associated with them. Amer Math Soc Transl Ser 2,1967,61:63-84

[9]Gustafson K,Weidmann J.On the essential spectrum.J Math Anal Appl,1969,25:121-127

[10]Jeribi A.Spectral Theory and Applications of Linear Operators and Block Operator Matrices.New York: Springer-Verlag,2015

[11]Jeribi A,Moalla N,Yengui S.S-essential spectra and application to an example of transport operators. Math Meth Appl Sci,2014,37(16):2341-2353

[12]Kato T.Perturbation theory for nullity,defciency and other quantities of linear operators.J Anal Math, 1958,6:261-322

[13]Markus A S.Introduction to the Spectral Theory of Polynomial Operator Pencils.Providence:American Mathematical Society,1988

[14]Mokhtar-Kharroubi M.Time asumptotic behavior and compactness in neutron transport theory.European Journal of Mechanics-B Fluids,1992,11(1):39-68

[15]Nussbaum R D.Spectral mapping theorems and perturbation theorem for Browding essential spectrum. Tran Amer Math Soc,1970,150:445-455

[16]Pelczynski A.On strictly singular and strictly cosingular operators.I.Strictly singular and strictly cosingular operators in C(Ω)-spaces.Bull Acad Polo Sci,1965,13:31-36

[17]Schechter M.Basic theory of Fredholm operators.Ann Scuola Norm Sup Pisa(3),1967,21:261-280

[18]Schechter M.Riesz operators and Fredholm perturbations.Bull Amer Math Soc,1968,74:1139-1144

[19]Schechter M.Principles of Functional Analysis.2nd ed.New York:Academic Press,2001

[20]Shapiro J,Schechter M.A generalized operational calculus developed from Fredholm operator theory.Trans Amer Math Soc,1973,175:439-467

[21]Shapiro J,Snow M.The Fredholm spectrum of the sum and product of two operators.Trans Amer Math Soc,1974,191:387-393

[22]Shkalikov A A,Tretter C.Spectral analysis for linear pencils N-λP of ordinary diferential operators. Math Nachr,1996,179:275-305

[23]Taylor A E.Spectral theory of closed distributive operators.Acta Math,1951,84(3):189-224

[24]Wolf F.On the invariance of the essential spectrum under a change of the boundary conditions of partial diferential operators.Indag Math,1959,21:142-147

∗Received August 19,2014;revised November 30,2014.