等差数列的凸性和对数凸性
2014-07-06石焕南
石焕南, 李 明
(1. 北京联合大学师范学院 电气信息系, 北京 100011; 2. 中国医科大学 数学教研室, 沈阳 110001)
等差数列的凸性和对数凸性
石焕南1, 李 明2
(1. 北京联合大学师范学院 电气信息系, 北京 100011; 2. 中国医科大学 数学教研室, 沈阳 110001)
研究了等差数列的凸性和对数凸性. 进而利用受控理论证明了一些等差数列不等式.
等差数列; 凸性; 对数凸性; 不等式; 受控
本文研究等差数列的凸性和对数凸性并利用受控理论证明一些等差数列不等式.
设{ai}是公差为d的等差数列, 则其通项ai=a1+(i−1)d, 前n项之和
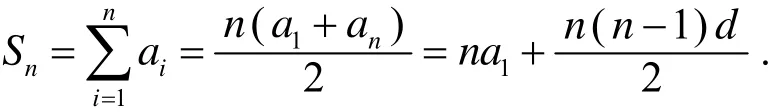
在本文中, Rn和分别表示n维实数集和n维正实数集, 并记表示非负整数集.先回忆一下数列的凸性和对数凸性的定义概念.
定义1.1[1,2]若实数列{ai} (有限的或无限的满足条件

则称{ai}是一个凸数列. 若不等式(1.1)反向, 则称数列{ai}是一个凹数列.
显然, 等差数列既是凸数列, 也是凹数列.
定义1.2[1,2]若非负实数列{ai}(有限的或无限的)满足条件
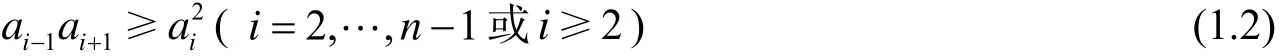
则称{ai}是一个对数凸数列. 若不等式(1.2)反向, 则称数列{ai}是一个对数凹数列.
1 主要结果
我们的主要结果是下述六个定理.
定理 1.1若{ai}是非负等差数列, 则{ai}是对数凹数列.
定理 1.2若{ai}是正项等差数列, 公差d≥0, 则既是凸数列, 也是对数凸数列.
定理 1.3若{ai}是非负等差数列, 公差d≥0, 则 {iai}既是凸数列, 也是对数凹数列.
定理 1.4若{ai}为正项等差数列, 则数列是凸数列.
定理1.5若非负等差数列{ai}的公差d≥0, 则其前n项和数列{Si}既是凸数列, 也是对数凹数列.
定理若{ai}为非负等差数列, 公差则{Ti}既是凸数列, 也是对数凸数列.
2 定义和引理
定义2.1[3,4]设x=(x1,…,xn),y=(y1,…,yn)∈Rn.
(ⅱ) x≤y表示对所有的i=1,…,n, xi≤yi.
定义 2.2[3,4]设 Ω⊂Rn, ϕ:Ω→R, 若∀x, y∈Ω,x≤y , 恒有ϕ(x)≤ϕ(y ), 则称ϕ为Ω上的增函数; 若−ϕ是Ω上的(严格)增函数, 则称ϕ为Ω上的减函数.
引理2.1[3,4]设x=(x1,…,xn)∈Rn,则

引理2.2[1,5]设n≥2, 数列{ak}是凸数列的充要条件为:当p≺q时, 恒有

引理2.3[1,6]设f:I⊂R→R是递增的凸函数, {ak}是凸集I上的凸数列,若p≺q, 则

引理2.4[5,6]非负数列{ak}是对数凸(凹)数列的充要条件为:若p≺q, 则

引理2.5若{ai}是对数凸数列, 则{ai}是凸数列.
证明因{ai}是对数凸数列, 即ai+1ai−1≥ai2. 于是,故{ai}是凸数列.引理2.6若{ai}是对数凹数列, 则是凸数列.
证明若{ai}是对数凹数列, 则是凸数列.
引理2.7设{ai}是单调递增的非负数列. 若{ai}是凸数列, 则{iai}也是凸数列; 若{ai}是对数凹数列, 则{iai}也是对数凹数列.
证明若{ai}是凸数列, 则ai+1+ai−1≥2ai; 又因{ai}单调递增, 有ai+1−ai−1≥0, 于是

故{iai}是凸数列.
若{ai}是对数凹数列, 则ai+1ai−1≤ai2, 于是

故{iai}是对数凹数列.
引理2.8[3,4]设 x, y∈Rn, x1≥x2≥…≥xn,若存在k, 1≤k≤n, 当i=1,2,…,k 时,xi≤yi, 当i=k+1,k+2,…,n 时, xi≥yi, 则x≺y.
引理2.9[3,4]设I⊂R为一个区间,x, y∈In⊂Rn, 则x≺y⇔∀凸(凹)函数g: I→R, 有

3 主要结果的证明
定理1.1的证明因a⋅a=(a+d)⋅(a−d)=a2−d2≤a2, 故{a}是对数凹数列.
定理1.2的证明由定理1.1,于是

定理1.3的证明由定理1.1知, {ai}是对数凹数列; 又d≥0, {ai}是递增的, 于是由引理2.7知{iai}既是凸数列, 也是对数凹数列.
定理1.4的证明由定理1.1知, 等差数列{ai}是对数凹数列, 由引理2.6知是凸数列.
定理1.5的证明因公差d≥0, 所以ai+1≥ai, 于是

故{Si}是凸数列.
因{ai}是对数凹数列, 所以

故{Si}也是对数凹数列.
定理1.6的证明因公差d≥0, 所以ai+1≥ai, 于是
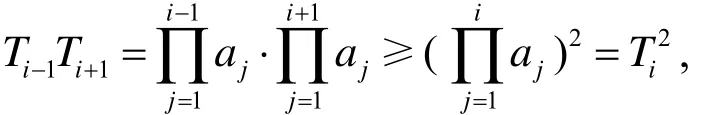
所以{Ti}是对数凸数列. 由引理2.5知{Ti}也是凸数列.
4 应用
命题4.1[7]设{ai}是正项等差数列, 则当r≥1或r≤0时, 有

当0 证明不妨设公差d≥0, 则a1≤a2≤…≤an, 于是由引理2.1与引理2.8, 有 当r≥1或r≤0时, xr是凸函数, 由引理2.9, 有2n由此即得(4.1)式.当0 命题4.2[8]设{ai}是正项等差数列, 公差d≥0, n为自然数, 则 证明由定理 1.2知是凸数列. 由引理2.8, 不难验证 事实上, 显然x1≥x2≥…≥x2n. 又 易见对于k=2n−1, 当i=1,2,…,k 时, xi≤yi, 当i=k+1,k+2,…,n 时, xi≥yi.这样x和y满足引理2.8的条件, 故有x≺y, 从而由引理2.2知(4.2)成立. 命题4.3[9]设{ai}是正项等差数列, n为自然数, 则 证明类似于(4.2), 可得 因等差数列{ai}是凸数列, 从而据引理2.2, 由(4.6), 有 因等差数列{−ai}是凸数列, 从而据引理2.2, 由(4.6), 有 即 结合(4.7)和(4.8)得(4.4). 命题4.4设{ai}是正项等差数列, 若n 证明条件n 命题4.5[10]设{ai}是正项等差数列, 公差d≥0, Sn是前n项和. 若n 证明由定理 1.5, {Si}既是凸数列, 也是对数凹数列. 由引理2.7知{iSi}既是凸数列也是对数凹数列, 余下证明类似于命题4.4, 从略. 命题4.6[11]设n>1, 则有下述阶乘不等式: 证明由定理1.6知正项等差数列{i}的前i项乘积数列{i!}是对数凸数列. 利用引理2.8不难验证 据引理2.4, 由上式即得(4.15)式. 由引理2.1有 和 易见 据引理2.4, 由(4.20), (4.21)和(4.22)分别可得(4.16), (4.17)和(4.18). 利用引理2.8不难验证 据引理2.4, 由上式可得 (4.19). 命题4.7(Khinchin不等式[11]) 设nk为非负整数, 且则 证明由定理1.6知正项等差数列{i}的前i项乘积数列{i!}是对数凸数列. 利用引理2.8不难验证 据引理2.4, 由(4.24)可得 即(4.23)成立. 命题4.8设n∈Z+, 则 证明由定理1.4知正项等差数列{i}的倒数数列是凸数列. 由引理2.1有 据引理2.2, 由(4.27)可得 当n>2时, 因 成立. 而当n=2时,故(4.25)成立. 利用引理2.8不难验证 于是 (4.25)和(4.26)两式分别加细了文献[12] 中第185页的两个不等式. [1] 石焕南. 受控理论与解析不等式[M]. 哈尔滨: 哈尔滨工业大学出版社, 2012 [2] PEČARIĆ J E, FRANK PROSCHAN AND TONG Y L.Convex functions, partial orderings, and statistical applications[M]. Academic Press.Inc., 1992 [3] 王伯英. 控制不等式基础[M]. 北京: 北京师范大学出版社, 1990 [4] Marshall A W, Olkin I, Arnold B C.Inequalities: theory of majorization and its application(Second Edition) [M]. New York: Springer Press, 2011 [5] 石焕南, 李大矛. 凸数列的一个等价条件及其应用[J]. 曲阜师范大学学报(自然版), 2001, 27(4): 4~6 [6] 石焕南. 凸数列的一个等价条件及其应用, Ⅱ[J]. 数学杂志, 2004, 24(4): 390~394 [7] 李 明. 关于正项等差数列幂和式的双边不等式[J]. 中国初等数学研究, 2014,5:41~42 [8] 盛宏礼. 正项等差数列一类分式不等式[J]. 中国初等数学研究, 2014, 5: 58~61 [9] 盛宏礼. 正项等差数列一类新不等式[J]. 数学通讯, 2011,11(下半月): 34~35 [10] 李玉群, 李永利. 关于正项等差数列方幂的若干不等式研究[J]. 济源职业技术学院学报, 2005, 4(3): 21~23 [11] 匡继昌. 常用不等式[M]. 第4版. 济南: 山东科学技术出版社, 2010 [12] 甘志国. 数列与不等式[M]. 哈尔滨: 哈尔滨工业大学出版社, 2014 Convexity and Logarithmic Convexity of Arithmetic Sequence SHI Huan-nan1, LI Ming2 The convexity and logarithmic convexity of the arithmetic sequence are studied. And then by using methods on the theory of majorization, some arithmetic sequence inequalities are proved. arithmetic sequence, convexity, logarithmic convexity, inequality, majorization O178 A 1672-5298(2014)03-0001-06 2014-07-07 石焕南(1948− ), 男, 湖南祁东人, 北京联合大学教授. 主要研究方向: 解析不等式


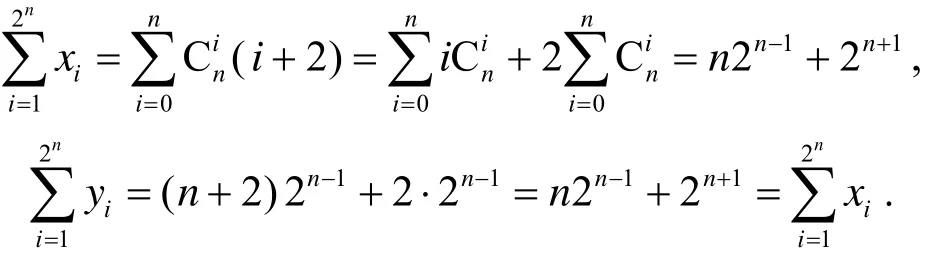





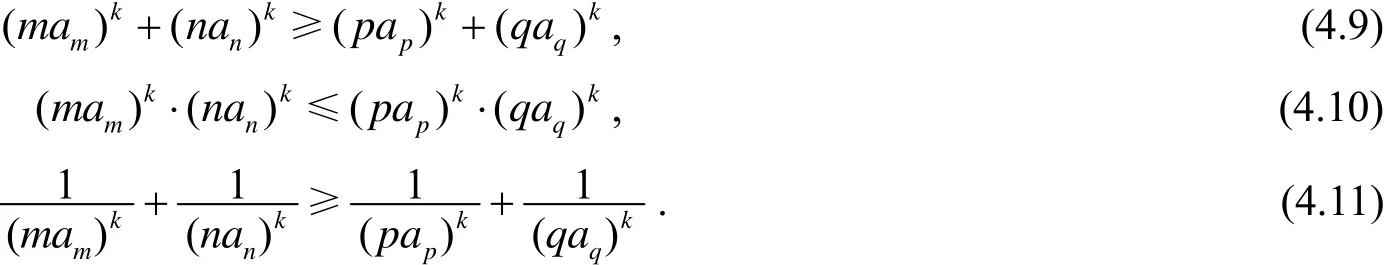






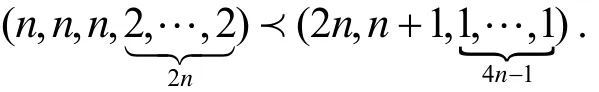




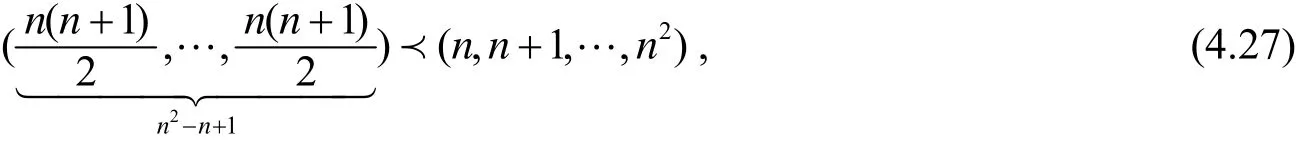




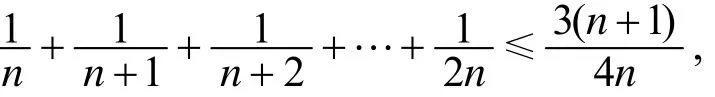
(1. Department of Electronic Information, Teacher's College of Beijing Union University, Beijing 100011, China; 2. Teaching & Research Group of Mathematics, China Medical University, Shenyang 110001, China)
