刘佩，袁泉，魏庆朝

(北京交通大学 土木建筑工程学院，北京，100044)

模型选择的标准是考察包含识别参数的模型对待识别结构进行描述的精确程度。数学模型是建立在对原始数据规律性挖掘的基础上的，但是，不同的建模方法对于原信息的规律把握不同，目前没有一个绝对优秀的建模方法，只能根据原始数据的特点选择相对合适的模型。对于模型选择在系统识别中的应用，需要根据具体识别问题的特点尝试得到，但由于对待识别结构系统的认识不足以及计算效率的差异，通常会产生识别参数的不当选取问题，或者得到多个不同的模型，导致模型对待识别结构的描述总是存在不完善之处。为了从中找出合理的模型，有必要对模型选择方法进行研究，来判断模型及其参数选择的优劣。过度复杂的模型可能使估计或者预测的方差偏大，而过度简单的模型又可能导致较大的估计或预测偏差，对于统计学中传统的模型选择方法，如AIC 和BIC等[1-2]，这些模型选择方法忽视了模型选择过程所带来的不确定性。传统的数据分析方法分成模型选择和基于选定的模型进行统计推断这2 个步骤。在进行第2步推断时，人们通常把第1 步选定的模型当作真实的数据产生过程而忽略了模型选择过程中的不确定性，导致低估实际的方差或均方误差。在系统识别中，通常采用的是在一系列模型中找到最优模型，但是，因为系统识别是反演问题，所以，很可能存在多个模型都可以对结构特性进行很好的模拟，因此，需要发展更具一般性的模型选择方法。张立涛等[3]结合结构识别问题的求解可采用正则化技术来改善其不适定的特点，引入不同识别结果所对应目标函数与识别结果的范数之间的对应规律作为先验条件，提出了一种基于L 曲线的模型确认方法。Goulet 等[4]提出了一种多模型方法来考虑不确定性及模型假定，该方法首先生成大量的候选模型，对反应进行预测，其次对结构进行静力试验，将模型不确定性及测量不确定性之和与设定的界限值对比，来判断接受或拒绝该模型。考虑到模型选择过程中的不确定性，基于贝叶斯理论的模型选择方法[5]可以同时考虑多个模型对结构反应预测的影响，还可以自动对复杂模型加以限制，定量计算得到选择各模型的概率。贝叶斯统计推断一般包括参数识别和模型选择：基于观测数据，通过贝叶斯理论或者结合一些抽样方法进行模型参数识别可以得到更新的模型参数概率密度函数；而通过贝叶斯理论进行模型选择可以评估各模型用来估计特定观测数据的概率能力[6-11]。本文作者通过推导用于计算各模型选择概率的证据表达式，建立基于贝叶斯理论的模型选择方法计算框架；当已知数据点足够多且为全局可识别情况时，可通过拉普拉斯渐近估计解法利用模型参数识别结果对证据进行计算。随后将基于贝叶斯理论的模型选择方法用于恢复力模型的选择中，首先是对双线性单自由度体系在地震波作用下的恢复力模型的选择，重点将基于贝叶斯理论的模型选择方法用于实测数据的模型选择，即采用实测滞回曲线数据的密肋复合墙试件的恢复力模型的选择，可利用各模型参数识别结果计算选择各模型的概率。

1 基于贝叶斯理论的模型选择方法

1.1 计算框架

令y 表示模拟的或实测的结构反应数据，模型选择 的 目 的 是 利 用 y 从 一 系 列 模 型μ={μj:j=1,2, …,NM}中选择最有可能的模型。根据贝叶斯定理，可以得到基于反应数据y 选择各模型的概率为

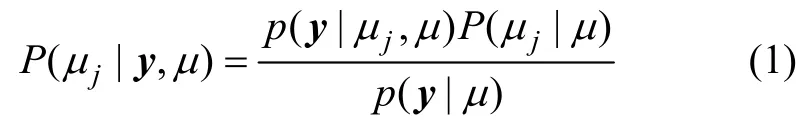
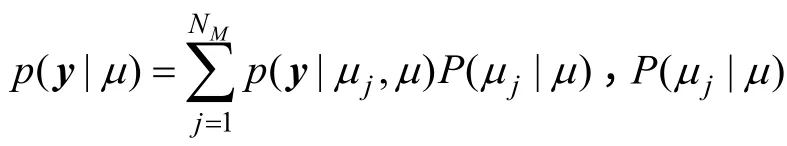
根据全概率公式，已知 y 时模型μj的证据p(y| μj)可表示为

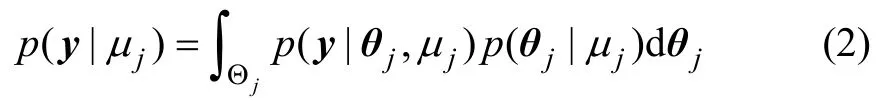
其中：j=1, 2, …, NM； θj表示模型 μj的参数矢量；p(θj| μj)为模型参数的先验概率密度函数，可根据经验确定； p(y | θj, μj)为模型参数的似然函数。

对于全局可识别情况，当数据y 足够多时， θj的后验概率密度函数可通过高斯分布进行估计[5]，则根据拉普拉斯渐近估计解法 p(y| μj)可近似表示为

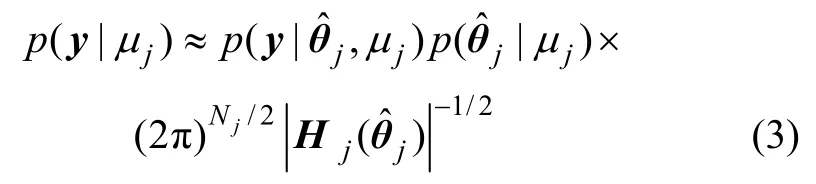
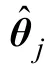
综上，根据贝叶斯模型选择方法，可根据p(y | μj) P(μj| μ)对各模型进行排序，最有可能的模型为使 p(y | μj) P(μj| μ)取得最大值的模型。模型证据 p(y| μj)可通过式(3)计算得到。模型先验分布P (μj| μ)可通过均匀分布来进行描述。

1.2 模型参数最有可能值的确定

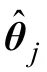
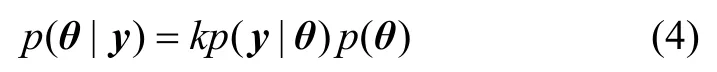
其中，k=1/ p(y)为正规化常数。则使后验分布取最大值，相当于使 -ln[ p(y | θ) p(θ)]取最小值。

假定模型计算反应为q，则

其中，e 为模型误差，假定e 在不同的测试点处为独立同分布的均值为0，标准差为σ 的高斯分布，则

则

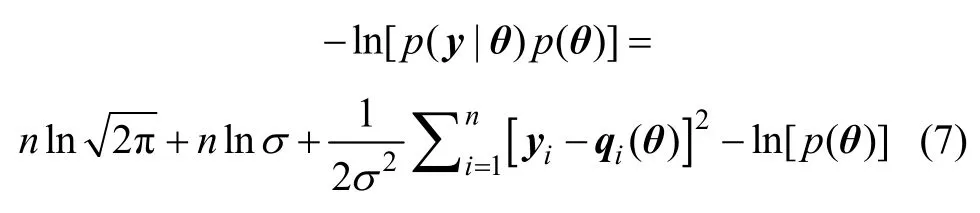
对式(7)的σ 求一阶导数并令其等于0，假定模型参数的先验分布为均匀分布，可得模型误差方差的最有可能值为

根据式(8)并通过Matlab 中的fminsearch函数对模型参数进行优化，可得到模型参数的最有可能值，进而可计算得到最有可能值处 -ln[ p(y | θ) p(θ)]的Hessian 矩阵。

2 所提方法在恢复力模型选择中的应用

本文将基于贝叶斯理论的模型选择方法用于恢复力模型的选择：(1) 受地震作用的双线性单自由度体系恢复力模型采用模拟输入输出数据；(2) 低周反复加载下密肋复合墙试件恢复力模型采用实测滞回曲线数据。

2.1 地震作用下的单自由度双线性体系

考虑单自由度双线性滞回体系的运动方程：

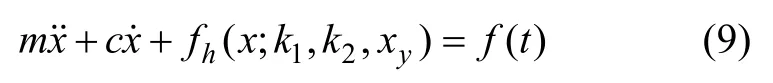
其中：x 为位移；m 为质量；c 为阻尼系数且假定为线性黏滞阻尼；k1为屈服前刚度；k2为屈服后刚度；xy为屈服位移；fh(x; k1, k2, xy)为恢复力，其特性见图1。

图1 单自由度体系双线性恢复力模型Fig.1 Bilinear restoring forcing model of SDOF system

假定已知反应数据为结构在地震作用下所得位移加上其5%均方差的高斯白噪声。考虑2 个恢复力模型，各模型均采用零均值的离散高斯白噪声作为预测误差模型。对模型1(μs,1)：双线性滞回体系，屈服前刚度k1＞0，屈服后刚度k2＞0，黏滞阻尼c=0，屈服位移为xy，预测误差标准差为 ση。对模型2(μs,2)：双线性滞回体系，屈服前刚度k1＞0，屈服后刚度k2＞0，黏滞阻尼c＞0，屈服位移为xy，预测误差标准差为 ση，该模型包含产生模拟反应数据的精确模型。

图2 地震波及其作用下体系的反应Fig.2 Earthquake record and corresponding displacement of system

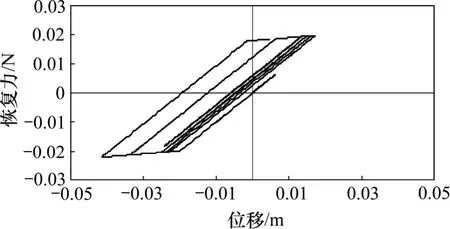
图3 地震波作用下体系的滞回环Fig.3 Hysteretic curve of system under earthquake record

假定各模型参数的先验分布相互独立且为均匀分布，k1的分布范围为(0, 2) N/m，k2的分布范围为(0, 0.5)N/m，c 的分布范围为(0, 0.1) N·s/m，xy的分布范围为(0, 0.1) m， ση的分布范围为(0, 0.01) m。

表1 所示为各模型在地震作用下根据式(8)识别得到的最有可能值。

地震作用下基于反应数据选择各模型的概率P (μj| y, μ)，j=1, 2 可根据式(1)计算得到，其中各模型的证据可根据式(3)计算得到，各模型的先验概率取P (μj| μ)=1/2，最终计算结果为P (μs,1| y, μ) ≈0，P (μs,2| y, μ)=1。结果表明，基于反应数据选择最有可能模型的概率接近于1，选择另外的模型概率近似为0，表明对该体系反应进行预测时，除最有可能模型外的模型都可以忽略。另外，该算例表明进行系统识别时，对于一个实际结构，最优的模型依赖于已知的系统数据，应该只对与系统识别中系统所受的激励水平接近的激励作用下的系统反应进行预测。

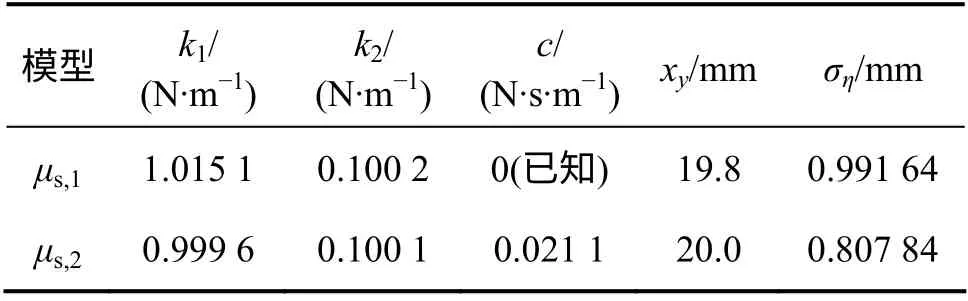
表1 单自由度体系各双线性恢复力模型参数的最有可能值Table 1 Most probable values of model parameters for each bilinear restoring force model of SDOF system

2.2 低周反复加载下的密肋复合墙试件

将基于贝叶斯理论的模型选择方法用于已知实测数据的恢复力模型选择中。作为该模型选择方法的研究基础，刘佩等[13]进行了基于贝叶斯理论的密肋复合墙试件恢复力模型参数的识别。

文献[13]中给出了7 块密肋复合墙试件在低周反复加载下发生剪切破坏的滞回曲线，标准密肋复合墙试件的实测滞回曲线见图4。从图4 可知：试件出现了明显的刚度退化、强度退化、滑移和捏拢现象。

图4 标准密肋复合墙试件实测滞回曲线Fig.4 Tested hysteretic curve of typical multi-gird composite wall specimen

根据以上现象，文献[13]提出了一种适用于剪切破坏的密肋复合墙体的恢复力模型，本文记为μm,1，见图5。模型达到极限荷载之前骨架曲线假定为双线性。模型的控制参数为：屈服前刚度k1，屈服后刚度k2，屈服荷载fy及其对应位移xy，极限荷载fu及其对应位移xu，考虑极限荷载后强度降低现象的参数Δd，考虑滑移捏拢现象的参数Δp 和Δs。模型的滞回规律假定为：(1) 达到极限荷载前，前一次循环结束之后再加载时和反向加载时，直线指向前一次循环的最大变形点；(2) 达到极限荷载后，前一次循环结束之后再加载时和反向加载时，直线指向由前一次循环的最大变形点与Δd 之和对应的位移及极限荷载确定的点的位置处；(3) 正向卸载及反向卸载直线通过考虑滑移捏拢参数轴正负Δs 位置前刚度为k1，之后指向力轴的考虑滑移捏拢参数负正Δp 位置处。

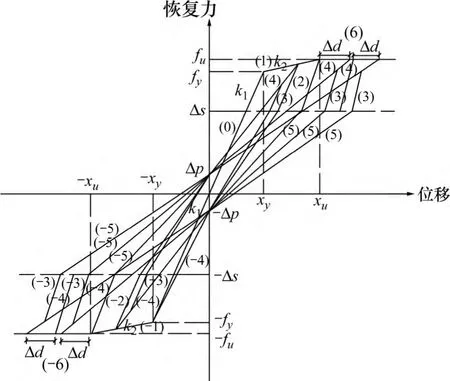
图5 密肋复合墙体的恢复力模型μ1Fig.5 Restoring force model μ1 of multi-grid composite walls

对于模型 μ1，若将极限荷载后强度降低现象通过将曲线指向上一循环的最大荷载降低一定的值与最大变形确定的位置表示，同样可以作为用来模拟密肋复合墙体反应的恢复力模型，即将考虑极限荷载后强度降低现象的参数Δd 变为ΔF[14]，本文将该恢复力模型记为μm,2，与 μ1的滞回规律假定(2)对比，模型 μ2将其变为达到极限荷载后，前一次循环结束之后再加载时和反向加载时，直线指向由前一次循环的最大变形点对应的位移及荷载与ΔF 之差确定的点的位置处。

这2 种模型都可以用来模拟构件的反应，但要对这2 种模型识别结果的差别定量化，则需要应用基于贝叶斯理论的模型选择方法确定，以便决定模拟构件反应时每种模型的权重。

采用标准密肋复合墙试件的实测滞回曲线作为已知数据，对选择2 个模型μm,1和μm,2的概率进行计算。

根据统计学理论中先验分布[15-16]的特点，其主要来源于经验和历史资料。本算例采用无信息先验分布，并根据试验数据确定模型参数先验分布的取值区间。设各模型参数的先验分布相互独立且为均匀分布：k1的分布范围为(5, 15) kN/mm，k2的分布范围为(0, 5)kN/mm，fy的分布范围为(45, 75) kN，Δp 的分布范围为(1, 7) kN，Δs 的分布范围为(5, 35) kN，Δd 的分布范围为(2, 6) mm，ΔF 的分布范围为(3, 9) kN，σ 的分布范围为(1, 3) mm。经计算发现，模型参数的先验分布对模型参数的最有可能值及Hessian 矩阵的结果没有影响。

根据贝叶斯理论，由式(8)识别得到的各模型参数的最有可能值见表2。

设模型先验概率P(μm,1| μ)=P(μm,2| μ)=1/2，则依据已知数据并根据式(1)得选择μm,1的概率为

选择μm,2的概率为

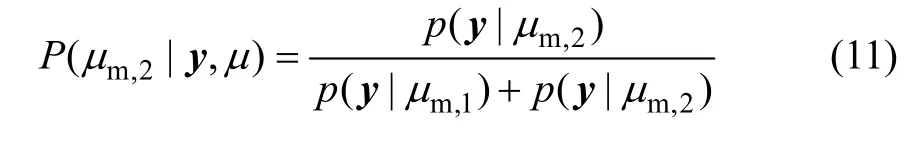
由式(10)和(11)可得计算结果为P (μm,1| y, μ)=0.697 7，P (μm,2| y, μ)=0.302 3。可见：对试件反应进行预测时，2 个模型均应考虑，可将依据已知数据选择各模型的概率作为权重系数，来考虑各模型在反应预测时所占的比例。

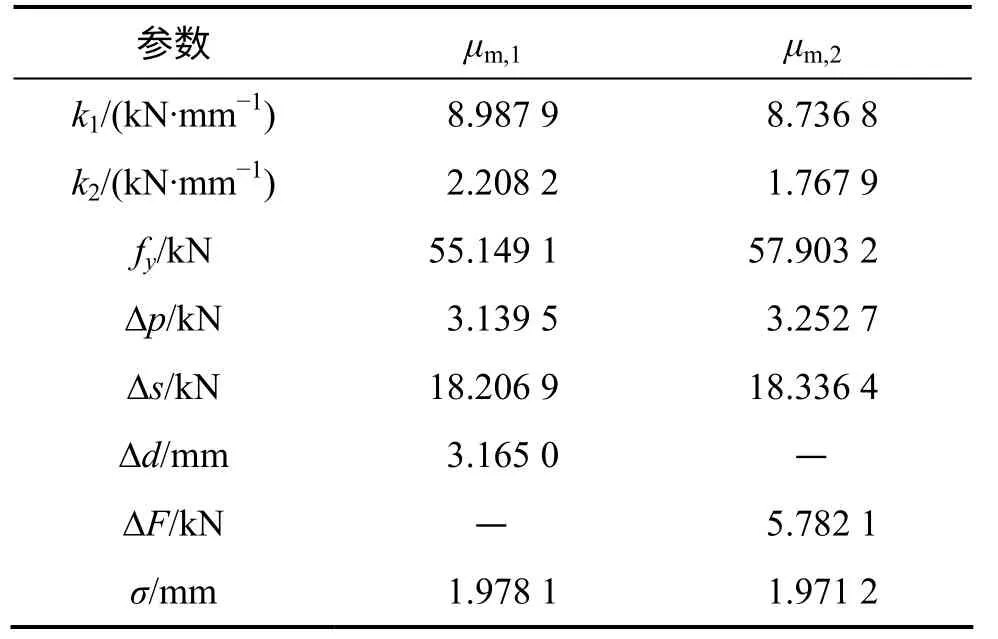
表2 密肋复合墙体各恢复力模型参数的最有可能值Table 2 Most probable values of model parameters for each restoring force model of multi-grid composite wall

3 结论

(1) 将基于贝叶斯理论的模型选择方法用于采用实测数据的恢复力模型的选择中，其中通过贝叶斯理论对恢复力模型参数进行了识别。

(2) 通过推导各模型的证据表达式，并结合贝叶斯定理得到选择各模型的概率，建立了基于贝叶斯理论的模型选择方法计算框架。该方法不仅可以识别得到模型参数的最有可能值，还可以识别得到最有可能的模型，并且考虑了模型及模型参数的不确定性。

(3) 根据双线性滞回体系在地震作用下响应的模拟数据对恢复力模型进行选择，若选择最有可能模型的概率接近于1，则进行反应预测时可以忽略其余模型的影响。

(4) 根据密肋复合墙试件在低周反复荷载下的实测滞回曲线数据对恢复力模型进行选择，得到了各模型的定量概率，结果表明：基于反应数据选择各模型的概率相差不大，此时需同时考虑各模型来进行反应预测，并可将选择各模型的概率作为反应预测的权重系数。

[1] Beck J L. Bayesian system identification based on probability logic[J]. Structural Control and Health Monitoring, 2010, 17(7):825-847.

[2] 张新雨, 邹国华. 模型平均方法及其在预测中的应用[J]. 统计研究, 2011, 28(6): 97-102.ZHANG Xinyu, ZOU Guohua. Model averaging method and its application in forecast[J]. Statistical Research, 2011, 28(6):97-102.

[3] 张立涛, 李兆霞, 张宇峰, 等. 结构识别计算中基于L 曲线的模型确认方法研究[J]. 振动与冲击, 2011, 30(11): 36-41.ZHANG Litao, LI Zhaoxia, ZHANG Yufeng, et al. Methodology of L-curve based model validation in structural identification[J].Journal of Vibration and Shock, 2011, 30(11): 36-41.

[4] Goulet J A, Kripakaran P, Smith F C. Multimodel structural performance monitoring[J]. ASCE Journal of Structural Engineering, 2010, 136(10): 1309-1318.

[5] Beck J L, Yuen K V. Model selection using response measurements: Bayesian probabilistic approach[J]. ASCE Journal of Engineering Mechanics, 2004, 130(2): 192-203.

[6] Mthembu L, Marwala T, Friswell M I, et al. Model selection in finite element model updating using the Bayesian evidence statistic[J]. Mechanical Systems and Signal Processing, 2011,25(7): 2399-2412.

[7] Cheung S H, Beck J L. Calculation of posterior probabilities for Bayesian model class assessment and averaging from posterior samples based on dynamic system data[J]. Computer-Aided Civil and Infrastructure Engineering, 2010, 25(5): 304-321.

[8] Ching J, Chen Y C. Transitional Markov chain Monte Carlo method for Bayesian model updating, model class selection, and model averaging[J]. ASCE Journal of Engineering Mechanics,2007, 133(7): 816-832.

[9] Cheung S H, Beck J L. Bayesian model updating using hybrid Monte Carlo simulation with application to structural dynamic models with many uncertain parameters[J]. ASCE Journal of Engineering Mechanics, 2009, 135(4): 243-255.

[10] Muto M, Beck J L. Bayesian updating and model class selection for hysteretic structural models using stochastic simulation[J].Journal of Vibration and Control, 2008, 14(1/2): 7-34.

[11] Beck J L, Au S K. Bayesian updating of structural models and reliability using Markov Chain Monte Carlo simulation[J].Journal of Engineering Mechanics, 2000, 128(4): 380-391.

[12] Beck J L, Katafygiotis L S. Updating models and their uncertainties. Ⅰ: Bayesian statistical framework[J]. Journal of Engineering Mechanics, 1998, 124(4): 455-461.

[13] 刘佩, 袁泉, 魏庆朝. 概率方法在恢复力模型参数识别中的应用分析[J]. 中南大学学报(自然科学版), 2013, 44(9):3843-3848.LIU Pei, YUAN Quan, WEI Qingchao. Application of a probabilistic approach to restoring force model parameter identification[J]. Journal of Central South University (Science and Technology), 2013, 44(9): 3843-3848.

[14] Qu Z, Ye L P. Strength deterioration models based on effective hysteretic energy dissipation for RC members under cyclic loading[C]// 7th International Conference on Urban Earthquake Engineering & 5th International Conference on Earthquake Engineering. Tokyo: Tokyo Institute of Technology, 2010:851-856.

[15] Siu N O, Kelly D L. Bayesian parameter estimation in probabilistic risk assessment[J]. Reliability Engineering and System Safety, 1998, 62(1/2): 89-116.

[16] 茆师松, 王静龙, 濮晓龙. 高等数理统计[M]. 2 版. 北京: 高等教育出版社, 2006: 368-372.MAO Shisong, WANG Jinglong, PU Xiaolong. Advanced mathematical statistics[M]. 2nd ed. Beijing: Higher Education Press, 2006: 368-372.