☉浙江省宁波市鄞州实验中学 蔡卫兵

“变”中“不变” 感受数学之灵韵

☉浙江省宁波市鄞州实验中学 蔡卫兵

习题教学是数学教学过程中不可缺少的环节，是向学生展示应用基础知识解决问题的窗口，是向学生渗透数学思想方法、传播解题技巧和技能的途径.因此数学课中习题教学应该是其中的主旋律，演奏好这条主旋律更需要我们去关注习题教学过程的设计，俯视问题——用活问题，仰视学生——以生为本，为学生搭建数学学习的典型框架，让学生主动地参与深层次的思维活动，形成基本的数学观念，努力构建充满灵动、富有韵味的课堂.但实际教学中，为了显示教师的“聪明”而让学生觉得解决问题的方法就像从魔术师的手里突然出现小白兔一样神奇，忽略了探究过程中的辅助、转换等环节的设计，从而出现“听而不懂”、“懂而不会”.所以探究之路上要慢走，等一下学生，尊重学生的自我认识，尊重学生独特的感受和经验，让学生获得知识和情感的双重体验，让学生收获研究数学问题的思想和方法，让学生在数学课堂教学中享受思维，让我们的数学课堂灵动而不失韵味.本文就一道常见习题的教学案例及其体会与大家分享.

一、教学过程简录

1.雾里看花——似懂非懂

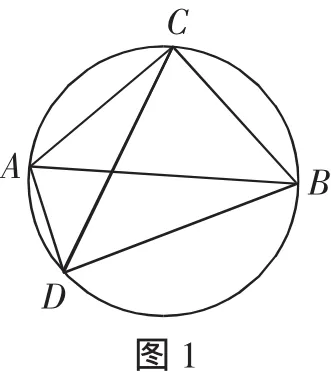
题目：如图1，⊙O为△ABC的外接圆，已知CA=CB，∠ACB=90°，点D为半圆上任意一点（D与C在AB的两侧），连接AD、BD、CD，请探究AD、 BD、CD三者之间的关系，并说明理由.

师：请大家仔细审题.

学生审题片刻.

师：通过审题，你能获得哪些信息？

生：等腰直角△ABC，AB为⊙O的直径，还有∠ADC=∠BDC=45°.

师：还有补充吗？

生：点D为半圆上任意一点.

师：根据这一信息，你如何探寻AD、BD、CD三者之间可能存在的关系呢？

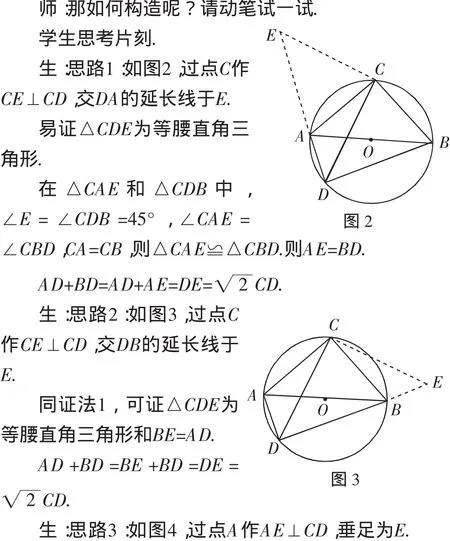
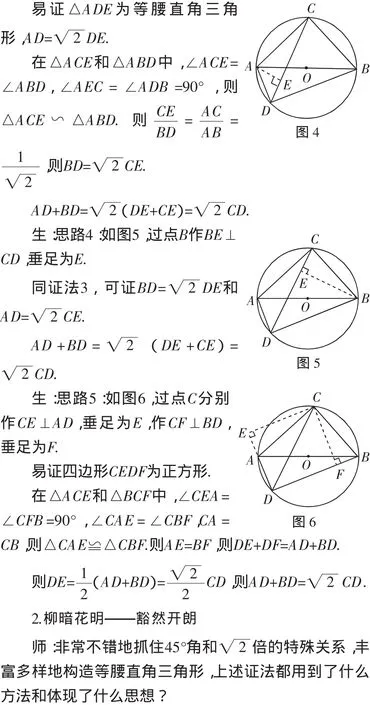
生：割补的数学方法和转化的数学思想.

师：对于线段之间的和差关系问题，常常可用割补转化的思想方法，我们还可以如何添辅助线呢？

生：思路6：图还是上面几种，比如图2，延长DA至点E，使得AE=BD，连接CE.

在△CAE和△CDB中，CA=CB，∠CAE=∠CBD，AE=BD，则△CAE≌△CBD.

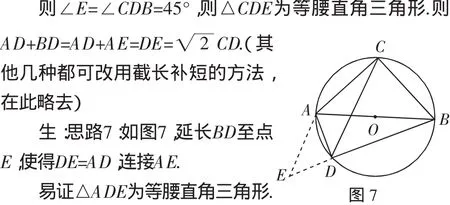
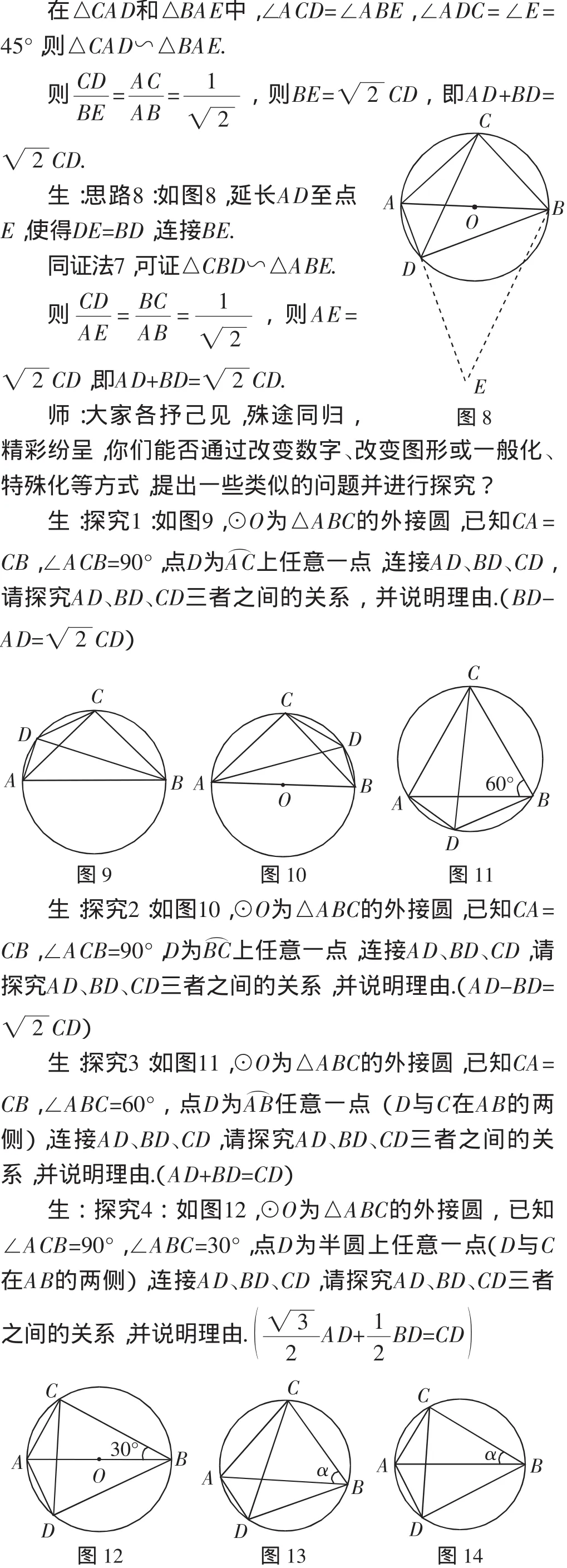
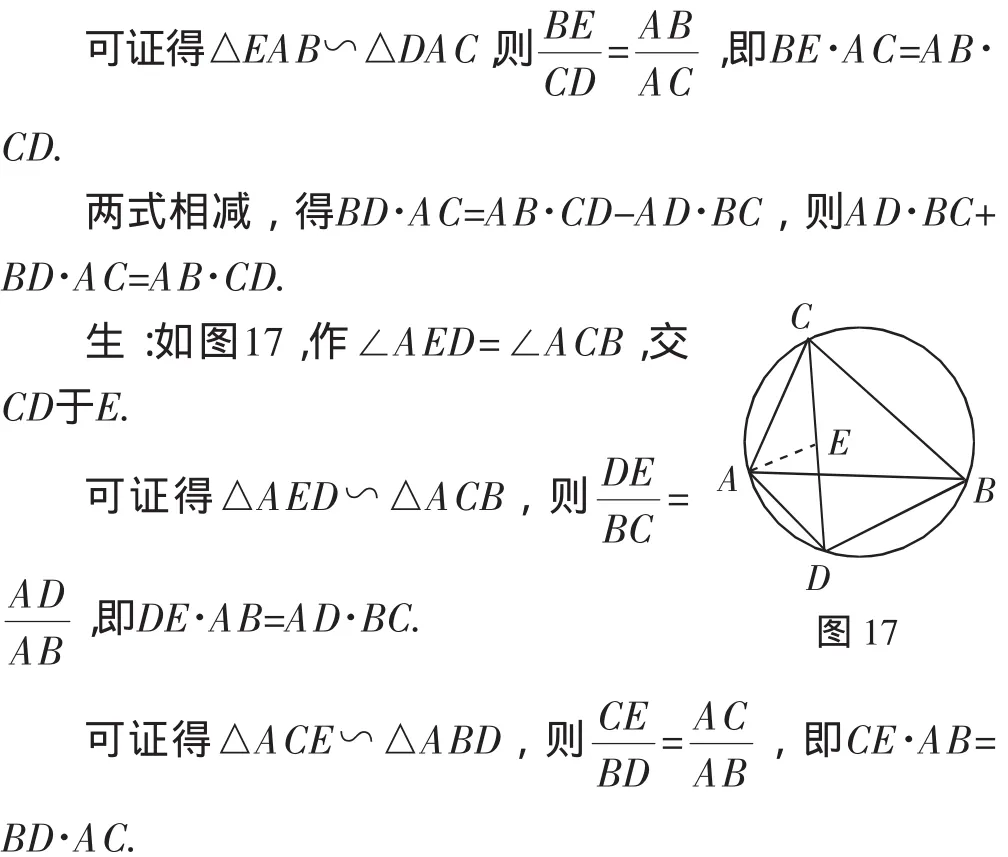
两式相加，得AD·BC+BD·AC=AB·CD.

师：真的非常厉害，你们又是怎么想出来的呢？这里的学习又体现了什么思想方法呢？

生：其实跟原题的解题思路差不多，也是在AD、BD或CD边上割补，原题抓住45°角构造等腰直角三角形，而构造的等腰直角三角形就是构造与△ABC相似的三角形，在这里的几种方法也都是构造与△ABC相似的三角形，只不过用了类比的数学方法和从特殊到一般的数学思想.

师：思路很清楚，想法很深刻，总结很精彩，活学活用，那么能否用文字语言来归纳一下这个神奇的关系呢？

生：圆内接四边形的两条对角线的积等于两组对边之积的和.

师：这是一个著名的几何定理——托勒密定理，非常佩服，其实同学们善于思考，勤于钻研，也能像数学家一样发现以你的名字命名的数学定理.

二、启发与反思

1.重视学生的体验，使课堂灵动而不失韵味

帮助学生积累数学活动经验是数学教学的重要目标，数学活动经验需要在“做”的过程和“思考”的过程中积淀，在数学活动中逐步积累.习题教学是知识熟练运用能力的积累，是交汇型知识综合运用能力的积累，是思想方法渗透经验的积累，是解决相似问题经验的积累.本案例中，从一道常见习题的解法探究到托勒密定理的惊奇发现与多种证法，确是“千淘万漉虽辛苦，吹尽狂沙始到金”.无论点D位置的变化中AD、BD、CD三者之间的关系的不变，还是截长补短的变化中数学思想方法的不变，无论已知条件的变化中探索AD、BD、CD三者之间的关系的不变，还是一般情形的图形变化中构造与△ABC相似的三角形的方法的不变，学生都有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程.这样不仅能积累数学解题经验，而且可获得基本的数学活动经验，将活动经验转化为能力，最终获得具有个性特征的感性认识、情感体验、数学意识、数学能力和数学素养，这样的课堂才是灵动而不失韵味的.

2.关注理性思维，数学课堂教学中的灵韵之笔

数学是思维的科学、思维的体操，数学的学习必须要通过思维去把握，去理解数学的实质.一题多解培养学生思维的发散性，一题多变培养学生思维的灵活性，理性思维的形成是以数学题目为载体，在题目的解决过程中形成的.本案例中，由点D为半圆上任意一点的信息的获取，自然想到特殊值法寻找AD、BD、CD三者之间的关系，由45°角和倍的特殊关系，自然想到等腰直角三角形的构造，线段之间的和差关系问题，常常考虑用割补转化的思想方法解决，从特殊条件到一般情形，自然想到类比构造与△ABC相似的三角形，呈现过程符合学生心理的认知规律，是合乎逻辑的思维方法，学生始终主动地参与深层次的思维活动以及数学地、合乎逻辑地、有条理地思考问题与解决问题的习惯与能力，它有明确的思维方向，有充分的思维依据，它既有发散，又有收缩，必将培养学生的运动思维，促进学生思维发展的连续性、递进性、发展性.在教学中，教师的讲解必须要贴近学生思维的发展水平，要遵循学生思维的发展规律，可使学生的认知思维过程自然流畅、水到渠成，从而能提高学生的思维能力，优化学生的思维结构.从AD、BD、CD三者之间的关系的探究到AD·BC+BD·AC=AB·CD六边之间有着神奇而简约的关系的发现，“形变而神不变”，经历美妙的数学思维的历程，呈现出数学之奇与数学之美，充分品味探究的魅力，体验数学学习的乐趣，这是数学课堂独特的“灵韵”之美.

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2.张建良.从“看出”向“证出”提升——一道复习题教学的启示［J］.中学数学（下），2013（10）.

3.成亮.“动中求定”感受数学之灵韵［J］.上海教育科研，2013（1）.

4.孙麟.浅谈初中生数学学习经验积累的探索［J］.中学数学（下），2013（10）.WG

·江苏省无锡市王华民名师工作室·