王丽丽

(温州大学 数学与信息科学学院，浙江 温州325035)

哈密顿体系下正交各向异性板弯曲的求解

王丽丽

(温州大学 数学与信息科学学院，浙江 温州325035)

运用哈密顿求解体系来求解正交各向异性板的弯曲问题，由板的挠度基本方程出发求得本征值，并根据本征值本身特点得到本征向量，进而求得问题的解，并讨论了该方法的特点。

哈密顿体系；正交各向异性；板弯曲

0 引言

目前很多文献讨论各向异性板的弯曲问题的方法。如张福范[1]用三角级数解正交各向异性板弯曲问题，冯立华[2]用利兹法求解正交各向异性矩形板的弯曲，王克林[3]用级数和叠加解得到正交各向异性板弯曲问题的解，张承宗[4]用复级数展开法求解了各向异性板的横向弯曲问题，王 震[5]用傅立叶级数法求解了各种边界条件下的正交各向异性板弯曲问题。上述一些方法中在求解不同矩形板的问题时不够系统而且要硬性事先选取弯曲挠度。本文将基于哈密顿体系来对正交各向异性板的弯曲问题进行推理直接可以获得弯曲解的表达方式进而获取一种较普遍适用的解法。

本文首先由板弯曲方程导入哈密顿体系，将问题的求解转入求解推导出的哈密顿对偶方程，将问题的解通过本征值和本征函数来表示，在求解本征向量时会依据本征值特点选取简洁的本征向量，并能够有规律并简洁的表述问题的解。

1 哈密顿体系的导入

本文在弹性力学基本方程的基础上来进行导入哈密顿体系。

1.1 板弯曲的挠度函数方程为：

其中，w表示板的挠度，q为横向外载荷，D11，D22，D12，D66为板的弯曲刚度。板内弯矩扭矩、剪力以及等效剪力分别表示

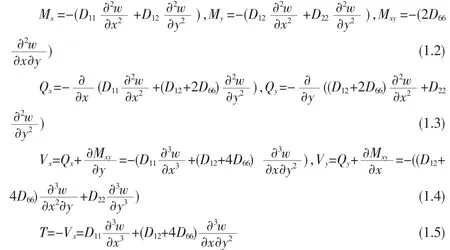
1.2 以[w，φx，T，Mx]T为对偶变量的方程

设v=[w，φx，T，Mx]T，对x求偏导，并结合(1.2)我们得到：

其中，

v=[w，φx，T，Mx]T为板的状态向量,f=[0 0 q 0]T为外力向量.“·”表示对x求偏导。矩阵H满足HT=JHJ，H是一个哈密顿算子矩阵,问题已经导入哈密顿体系。式子(2.3)是求解薄板的哈密顿对偶方程。

2 求解薄板的哈密顿对偶方程

2.1 求解式子(2.3)的齐次方程为

其中，Y(y)=[w(y)，φx(y)，T(y)，Mx(y)]T.ξ与Y(y)为需求非零本征值与本征向量。令ξ=0，解出Y(y)=0.对于问题求解无意义故不需要考虑ξ=0的情况。本征解转化为求解如下的特征方程：

可得到方程(2.5)根：λ1，2=±iβ1ξ，λ3，4=±iβ2ξ，(β1＜β2)，相应的通解形式：

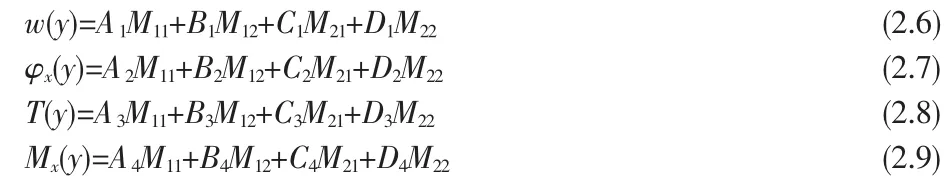
其中，M11=cos(β1ξy)，M12=sin(β1ξy)，M21=cos(β2ξy)，M22=sin(β2ξy)

而由式(2.4)得到：

Ai，Bi，Ci，Di(i=1-4)为常数但之间有关联，可由式(2.4)来确定它们之间数量关系。

2.2 以对边简支作为求解示例

对于对边简支板，y方向的简支边界条件为：

将式(2.6)代入条件(2.11)得关于A1，B1，C1，D1的齐次线性方程组

其中，m11=cos(β1ξb/2)，m12=sin(β1ξb/2)，m21=cos(β2ξb/2)，m22=sin(β2ξb/2)

因为A1，B1，C1，D1不可全部为零而需要取得非平凡解，故(2.12)系数行列式为零。得到关于ξ的超越方程。不考虑ξ=0.得到：

sin(β1ξb)sin(β2ξb)=0.解得非零本征值：

将求得的根ξn代入方程(2.12)可以得到系数的特点，进而得出

A1，B1，C1，D1简洁的非平凡解。具体方法如下：

（1）特征值ξn

取A1=1，B1=0，C1=0，D1=0，再由(2.10)求得Ai，Bi，Ci，Di(i=2-4)

取A1=0，B1=1，C1=0，D1=0，再由(2.10)求得Ai，Bi，Ci，Di(i=2-4)

（2）特征值ξn=-ξn

n=1，3，5…取A1=-1，B1=0，C1=0，D1=0

n=2，4，6…取A1=0，B1=1，C1=0，D1=0(此处取B1=1是根据后面本征向量来取得)

（3）特征值ξn*

注：这里的是Ai，Bi，Ci，Di(i=1-4)简单符号表达具体问题中与本征值和n有关。它们的选取完全依据本征值做了全面的选取，而不是随便解得。故对后面的求解更全面。

由(2.4)得

3 算例

以四边简支的正交各向异性的边长为1的方板为例。

D22=3.9D11，D66=0.85D11，D12=v2D11，v2=0.3。代入式子(2.5)，(2.13)解得非零本征值。取满足非齐次方程(2.3)的特解

x方向的边界条件为：

［1］张福范.弹性薄板[M].北京：科学出版社，1984.

［2］冯立华，杨加明，戴良忠，王旭.利兹法求解正交各向异性矩形板的弯曲[J].失效分析与预防，2012，7(4)：207-212.

［3］王克林，刘俊卿，赵东.平板的弯曲振动和屈曲[M].北京：冶金工业出版社，2006.

［4］张承宗，杨光松.各向异性板结构横向弯曲一般解析解[J].力学学报，1996，28 (4)：47-48.

［5］王震，张为民，刘新东.傅立叶级数法求解正交各向异性板弯曲问题[J].山西建筑，2008，34(29)：12-13.

［6］姚伟岸，钟万勰.辛弹性力学[M].北京：高等教育出版社，2002.

［7］钟万勰，弹性力学求解新体系[M].大连：大连理工大学出版社，1995.

［8］徐芝纶.弹性力学[M].北京：高等教育出版社，2002.

［9］苏滨.哈密顿体系在各向异性板弯曲问题中的应用[D].大连理工大学，2000.

［10］钟阳，周纯秀，刘 伟.求解弹性矩形薄板问题的辛几何法[J].哈尔滨工业大学学报，2004，36(4)：505-507.

［11］李锐.矩形板问题的Hamilton求解方法[D].大连理工大学，2012.

Orthotropic Anisotropic Plate Bending Under Hamiltonian System

WANG Li-li
(College of mathematics and information science,Wenzhou University,Wenzhou Zhejiang 325035,China)

The Hamiltonian solution system to the bending problem of orthotropic plates,the basic equations of deflection plates to obtain eigenvalues and Intrinsic value itself,according to the characteristics of the eigenvector,and then get the solution of the problem,and discusses the characteristics of the method.

Hamiltonian system；Orthotropic anisotropic；Plate bending

汤静］